GW parallel strategies
This modules contains very general discussions of the parallel environment of Yambo. In this tutorial we will see how to setup the variables governing the parallel execution of yambo in order to perform efficient calculations in terms of both cpu time and memory to solution. As a test case we will consider the hBN 2D material. Because of its reduced dimensionality, GW calculations turns out to be very delicate. Beside the usual convergence studies with respect to k-points and sums-over-bands, in low dimensional systems a sensible amount of vacuum is required in order to treat the system as isolated, translating into a large number of plane-waves. As for other tutorials, it is important to stress that this tutorial it is meant to illustrate the functionality of the key variables and to run in reasonable time, so it has not the purpose to reach the desired accuracy to reproduce experimental results. Moreover please also note that scaling performance illustrated below may be significantly dependent on the underlying parallel architecture. Nevertheless, general considerations are tentatively drawn in discussing the results.
Getting familiar with yambo in parallel
Let's start by copying the tutorial files in the cluster and unzip them in the folder you will run the tutorial.
$ mkdir YAMBO_TUTORIALS $ cd YAMBO_TUTORIALS $ cp $path/hBN-2D-para.tar.gz ./ $ tar -zxvf hBN-2D-para.tar.gz $ cd ./hBN-2D-para/YAMBO
Under the YAMBO folder, together with the SAVE folder, you will see the run.sh script
$ ls parse_qp.py parse_ytiming.py SAVE
First, run the initialization as usual. Then you need to generate the input file for a GW run.
$ yambo -g n -p p -F yambo_gw.in
After setting the variables in red, the new input file should look like the following:
$ cat yambo_gw.in
ppa # [R Xp] Plasmon Pole Approximation
gw0 # [R GW] GoWo Quasiparticle energy levels
HF_and_locXC # [R XX] Hartree-Fock Self-energy and Vxc
em1d # [R Xd] Dynamical Inverse Dielectric Matrix
X_Threads= 0 # [OPENMP/X] Number of threads for response functions
DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles
SE_Threads= 0 # [OPENMP/GW] Number of threads for self-energy
EXXRLvcs= 21817 RL # [XX] Exchange RL components
VXCRLvcs= 21817 RL # [XC] XCpotential RL components
Chimod= "" # [X] IP/Hartree/ALDA/LRC/BSfxc
% BndsRnXp
1 | 300 | # [Xp] Polarization function bands
%
NGsBlkXp= 4 Ry # [Xp] Response block size
% LongDrXp
1.000000 | 0.000000 | 0.000000 | # [Xp] [cc] Electric Field
%
PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy
% GbndRnge
1 | 300 | # [GW] G[W] bands range
%
GDamping= 0.10000 eV # [GW] G[W] damping
dScStep= 0.10000 eV # [GW] Energy step to evaluate Z factors
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g")
%QPkrange # [GW] QP generalized Kpoint/Band indices
1| 4| 1| 8|
%
Now you need to create a submission script. here below an example (run.sh) based on the SLURM scheduler. In the case of other schedulers, the header should be updated accordingly.
$ cat run.sh #!/bin/bash #SBATCH -N 1 #SBATCH -t 06:00:00 #SBATCH -J test #SBATCH --partition=<queue name> #SBATCH --tasks-per-node=1 #SBATCH --cpus-per-task=1 nodes=1 tasks_per_node=1 nthreads=1 ncpu=`echo $nodes $tasks_per_node | awk '{print $1*$2}'` module purge module load <needed modules> module load <more modules> bindir=<path to yambo bindir> export OMP_NUM_THREADS=$nthreads label=MPI${ncpu}_OMP${nthreads} jdir=run_${label} cdir=run_${label}.out filein0=yambo_gw.in filein=yambo_gw_${label}.in cp -f $filein0 $filein cat >> $filein << EOF DIP_CPU= "1 $ncpu 1" # [PARALLEL] CPUs for each role DIP_ROLEs= "k c v" # [PARALLEL] CPUs roles (k,c,v) DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles X_and_IO_CPU= "1 1 1 $ncpu 1" # [PARALLEL] CPUs for each role X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v) X_and_IO_nCPU_LinAlg_INV= $ncpu # [PARALLEL] CPUs for Linear Algebra X_Threads= 0 # [OPENMP/X] Number of threads for response functions SE_CPU= " 1 $ncpu 1" # [PARALLEL] CPUs for each role SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b) SE_Threads= 0 EOF echo "Running on $ncpu MPI, $nthreads OpenMP threads" mpirun -np $ncpu $bindir/yambo -F $filein -J $jdir -C $cdir
As soon as you are ready to submit the job.
$ sbatch run.sh
Yambo calculates the GW-qp corrections running on 1 MPI process with a single thread. As you can see, monitoring the log file produced by yambo, the run takes some time, although we are using minimal parameters.
The status of the jobs can be monitored via:
$ squeue -u $USER # to inspect the status of jobs
# (hint: make a unix alias, if you like)
$ scancel <jobid> # to delete jobs in the queue
Pure MPI scaling with default parallelization scheme
Meanwhile we can run the code in parallel. Let's use consider the case of a node having 16 cores (you can try to adapt the following discussion to the actual maximum number of cores/node you have in your system). As a first run, we'll use 16 MPI tasks, still with a single thread. To this end modify the run.sh script changing
#SBATCH --tasks-per-node=16 #SBATCH --cpus-per-task=1
ntasks_per_node=16 nthreads=1
This time the code should be much faster.
Once the run is over try to run the simulation also on 2, 4, 8 MPI tasks.
Each time, please remember to change both the number of tasks per node both in the header and in the ntasks_per_node variable.
Finally, you can try to produce a scaling plot.
To analyze the data you can use the phyton script parse_ytiming.py run which is provided.
You can use it running
$ ./parse_ytiming.py run*/r-*
You should obtain something like that (but with more columns)
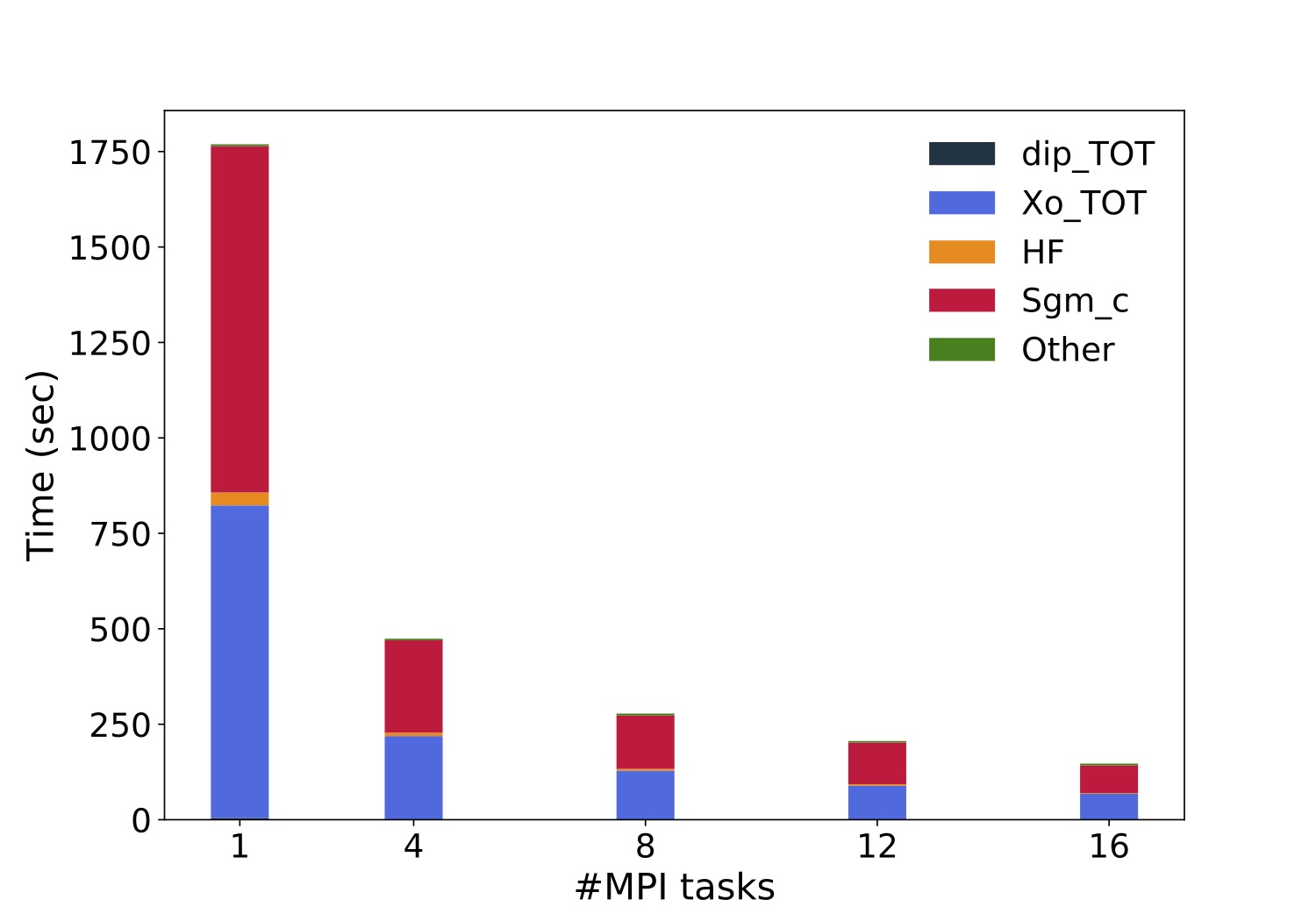
# ncores dip Xo X io_X io_WF Sgm_x Sgm_c (REDUX) WALL_TIME
1 4.7337s 13m39.00s 0.1500s 0.0241s 0.2487s 34.2143s 15m7.00s 0.0000s 29m29s
4 1.6019s 218.7982s 0.0882s 0.0283s 0.2077s 9.3338s 242.4438s 0.0001s 07m54s
8 1.0755s 127.3209s 0.0974s 0.0291s 0.2134s 5.4490s 140.7788s 0.6926s 04m38s
12 0.7510s 89.1649s 0.1015s 0.0299s 0.2068s 4.2961s 109.1227s 0.0007s 03m26s
16 0.7653s 68.2550s 0.1048s 0.0309s 0.2463s 2.9211s 72.6220s 0.2799s 02m27s
Plot the execution time vs the number of MPI tasks
and check (do a log plot) how far you are from the ideal linear scaling.
Below a similar plot produced on a local cluster equipped with two Intel(R) Xeon(R) Silver 4208 CPU @ 2.10GHz processors per node (16 physical cares/node).
tips:
- not all runlevels scale in in the same way
- you should never overload the available number of cores
Pure OpenMP scaling
Next step is instead to check the OpenMP scaling. Set back
#SBATCH --tasks-per-node=1 #SBATCH --cpus-per-task=16
and now use
ntasks_per_node=1 nthreads=16
Since we are already using 16 threads, we cannot also distribute among MPI tasks, i.e. ncpu will result equal to 1. Try setting nthreads to 16, 8, 4 and 2 and again to plot the execution time vs the number of threads using the python script. Again you should be able to produce data similar to the following. In the following we stopped increasing the number of threads up to 8 because of the specific architecture used in the runs (a dual socket machine with 8 cores/socket).
# ncores threads dip Xo X io_X io_WF Sgm_x Sgm_c WALL_TIME
1 1 4.7337s 13m39.00s 0.1500s 0.0241s 0.2487s 34.2143s 15m7.00s 29m29s
2 2 3.1971s 549.1491s 0.2248s 0.0298s 0.2491s 17.6552s 584.3692s 19m17s
4 4 2.9419s 358.5202s 0.1928s 0.0289s 0.2590s 9.2010s 421.2219s 13m15s
8 8 2.7992s 344.3342s 0.2332s 0.0325s 0.2543s 5.4334s 362.6982s 11m58s
tips:
- OpenMP usually shares the memory among threads, but not always
- you should never overload the available number of cores
- in principle, we could overload the cores setting more threads than the available total number of cores since a single core allows multi-thread operations
MPI vs OpenMP scaling
Which is scaling better ? MPI or OpenMP? How is the memory distributed?
Now you can try running simulations with hybrid strategies. Try for example setting:
#SBATCH --tasks-per-node=8 #SBATCH --cpus-per-task=2
ntasks_per_node= 8 nthreads= 2
We can try to do scaling keeping the total number of threads per node (ntasks_per_node * nthreads) equal to 16. Parsing the data we will obtain something similar to
# ncores MPI threads dip Xo X io_X io_WF Sgm_x Sgm_c WALL_TIME
16 2 8 3.6816s 386.0552s 0.0856s 0.0268s 0.2163s 18.9077s 530.0875s 15m43s
16 4 4 0.9950s 82.5070s 0.1098s 0.0299s 0.2051s 3.0837s 122.6565s 03m32s
16 8 2 0.8524s 72.6708s 0.0986s 0.0293s 0.2282s 3.0379s 88.1589s 02m48s
16 16 1 0.7653s 68.2550s 0.1048s 0.0309s 0.2463s 2.9211s 72.6220s 02m27s
As you can see here the total CPU time decreases more and more moving the parallelization from the OpenMP to the MPI level. Sigma_c in particular scales better. Nevertheless, note that the relative performance of the different parallel configurations may strongly depend on the actual machine you are running on.
However, CPU time is not the only parameter you need to check.
The total memory usage is also very critical since the GW method may have a large memory footprint.
If you have compiled yambo with the flag --enable-memory-profile, the memory usage is tracked and the maximum allocated mem
is printed in the report file, and can be extracted typing:
$ grep "Max memory used" <report_file>
In general yambo can distribute memory when using MPI parallelism (though the actual amount depends on the distribution of MPI tasks across MPI levels). Nevertheless, some memory replication is still present. In general, within the node OpenMP helps in easing the memory usage. Therefore, in cases where the node memori is tight, one may consider changing some MPI tasks for OpenMP threads within the node.
Using a hybrid scheme you may also consider running yambo on mode than one node.
To run on two nodes for example you need to set
#SBATCH -N 2 nodes=2
accordingly you can now set
nthreads= 4
This time you will use 32 cores with (16 per node) 4 OpenMP threads and 2*16/4=8 MPI tasks.
tips:
- in real life calculations running on n_cores > 100, it is a good idea to adopt a hybrid approach
- with OpenMP, you cannot exit the single node, with MPI you can
Advanced: Comparing different parallelization schemes (optional)
Up to now, we used the default parallelization scheme. Yambo also allows you to tune the parameters which controls the parallelization scheme. To this end, you can open again the job.sh script and modify the section where the yambo input variables are set
X_and_IO_CPU= "1 1 1 $ncpu 1" # [PARALLEL] CPUs for each role X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v) #X_and_IO_nCPU_LinAlg_INV= $ncpu # [PARALLEL] CPUs for Linear Algebra X_Threads= 0 # [OPENMP/X] Number of threads for response functions DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles SE_CPU= "1 1 $ncpu" # [PARALLEL] CPUs for each role SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b) SE_Threads= 0
In particular, "X_and_IO_CPU" sets how the MPI Tasks are distributed in the calculation of the response function. The possibilities are shown in the "X_and_IO_ROLEs". The same holds for "SE_CPU" and "SE_ROLEs" which control how MPI Tasks are distributed in the calculation of the response function.
Please try different parallelization schemes and check the performances of Yambo. In doing so, you should also change the jobname in the run.sh script
label=MPI${ncpu}_OMP${nthreads}_scheme1
Using the python script, you can then check how speed, memory and load balance between the CPUs are affected. For more details, see also the Parallel module
tips:
- the product of the numbers entering each variable (i.e. X_and_IO_CPU and SE_CPU) times the number of threads should always match the total number of cores (unless you want to overload the cores taking advantage of multi-threads)
- using the X_Threads and SE_Threads variables, you can think about setting different Hybrid schemes in between the screening and the self-energy runlevel.
- memory better scales if you parallelize on bands (c v b)
- parallelization on k-points performs similarly to parallelization on bands, but memory requires more memory
- parallelization on q-points requires much less communication in between the MPI tasks. It may be useful if you run on more than one node and the internode connection is slow
| Prev: Tutorials Home | Now: Tutorials Home --> GW Parallel | Next: GW Convergence |