GW parallel strategies: Difference between revisions
| Line 273: | Line 273: | ||
tips: <br> | tips: <br> | ||
- the product of the numbers entering each variable (i.e. X_all_q_CPU and SE_CPU) times the number of threads should always match the total number of cores (unless you want to overload the cores taking advantage of multi-threads) | |||
- using the X_Threads and SE_Threads variables you can think about setting different Hybrid schemes in between the screening and the self-energy runlevel. | |||
- memory better scales if you parallelize on bands (c v b) <br> | - memory better scales if you parallelize on bands (c v b) <br> | ||
- parallelization on k-points performs similarly to parallelization on bands, but memory requires more memory <br> | - parallelization on k-points performs similarly to parallelization on bands, but memory requires more memory <br> | ||
Revision as of 08:05, 26 April 2017
In this tutorial we will see how to setup the variables governing the parallel execution of yambo in order to perform efficient calculations in terms of both cpu time and memory to solution. As a test case we will consider the hBN 2D material. Because of its reduced dimensionality, GW calculations turns out to be very delicate. Beside the usual convergence studies with respect to k-points and sums-over-bands, in low dimensional systems a sensible amount of vacuum is required in order to treat the system as isolated, translating into a large number of plane-waves. As for other tutorials, it is important to stress that this tutorial it is meant to illustrate the functionality of the key variables and to run in reasonable time, so it has not the purpose to reach the desired accuracy to reproduce experimental results. Moreover please also note that scaling performance illustrated below may be significantly dependent on the underlying parallel architecture. Nevertheless, general considerations are tentatively drawn in discussing the results.
Getting familiar with yambo in parallel
If you are not inside bellatrix, please follow the instructions in the tutorial home. If you are inside bellatrix and in the proper folder
[cecam.school01@bellatrix yambo_YOUR_NAME]$ pwd /scratch/cecam.schoolXY/yambo_YOUR_NAME
you can proceed. First you need to obtain the appropriate tarball
$ cp /scratch/cecam.school/hBN-2D-para.tar.gz ./ (Notice that this time there is not XY!) $ tar -zxvf hBN-2D-para.tar.gz $ ls YAMBO_TUTORIALS $ cd YAMBO_TUTORIALS/hBN-2D/YAMBO
To run a calculation on bellatrix you need to go via the queue system as explained in the Tutorials home. Under the YAMBO folder, together with the SAVE folder, you will see the run.sh script
$ ls parse_yambo.py parse_qp.py run.sh SAVE
First run the initialization as usual. Then you need to generate the input file for a GW run.
$ yambo -g n -p p -F yambo_gw.in
The new input file should look like the folllowing. Please remove the lines you see below with a stroke and set the parameters to the same values as below
$ cat yambo_gw.in # # # Y88b / e e e 888~~\ ,88~-_ # Y88b / d8b d8b d8b 888 | d888 \ # Y88b/ /Y88b d888bdY88b 888 _/ 88888 | # Y8Y / Y88b / Y88Y Y888b 888 \ 88888 | # Y /____Y88b / YY Y888b 888 | Y888 / # / / Y88b / Y888b 888__/ `88_-~ # # # GPL Version 4.1.2 Revision 120 # MPI+OpenMP Build # http://www.yambo-code.org # ppa # [R Xp] Plasmon Pole Approximation gw0 # [R GW] GoWo Quasiparticle energy levels HF_and_locXC # [R XX] Hartree-Fock Self-energy and Vxc em1d # [R Xd] Dynamical Inverse Dielectric MatrixX_Threads= 32 # [OPENMP/X] Number of threads for response functionsDIP_Threads= 32 # [OPENMP/X] Number of threads for dipolesSE_Threads= 32 # [OPENMP/GW] Number of threads for self-energyEXXRLvcs= 21817 RL # [XX] Exchange RL components Chimod= "" # [X] IP/Hartree/ALDA/LRC/BSfxc % BndsRnXp 1 | 200 | # [Xp] Polarization function bands % NGsBlkXp= 4 Ry # [Xp] Response block size % LongDrXp 1.000000 | 0.000000 | 0.000000 | # [Xp] [cc] Electric Field % PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy % GbndRnge 1 | 200 | # [GW] G[W] bands range % GDamping= 0.10000 eV # [GW] G[W] damping dScStep= 0.10000 eV # [GW] Energy step to evaluate Z factors DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") %QPkrange # [GW] QP generalized Kpoint/Band indices 1| 1| 3| 6| %
You can now open the submission script and the submission script
$ cat run.sh #!/bin/bash #SBATCH -N 1 #SBATCH -t 06:00:00 #SBATCH -J test #SBATCH --reservation=cecam_course #SBATCH --tasks-per-node=1 nodes=1 nthreads=1 ncpu=`echo $nodes $nthreads 1 | awk '{print $1*$3/$2}'` module purge module load intel/16.0.3 module load intelmpi/5.1.3 bindir=/home/cecam.school/bin/ export OMP_NUM_THREADS=$nthreads label=MPI${ncpu}_OMP${nthreads} jdir=run_${label} cdir=run_${label}.out filein0=yambo_gw.in filein=yambo_gw_${label}.in cp -f $filein0 $filein cat >> $filein << EOF X_all_q_CPU= "1 1 $ncpu 1" # [PARALLEL] CPUs for each role X_all_q_ROLEs= "q k c v" # [PARALLEL] CPUs roles (q,k,c,v) X_all_q_nCPU_LinAlg_INV= $ncpu # [PARALLEL] CPUs for Linear Algebra X_Threads= 0 # [OPENMP/X] Number of threads for response functions DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles SE_CPU= " 1 1 $ncpu" # [PARALLEL] CPUs for each role SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b) SE_Threads= 0 EOF echo "Running on $ncpu MPI, $nthreads OpenMP threads" srun -n $ncpu -c $nthreads $bindir/yambo -F $filein -J $jdir -C $cdir
As soon as you are ready submit the job.
$ sbatch run.sh
Yambo calculates the GW-qp corrections running on 1 MPI process with a single thread. As you can see, monitoring the log file produced by yambo, the run takes some time, although we are using minimal parameters.
Pure MPI scaling with default parallelization scheme
Meanwhile we can run the code in parallel. Let's use 16 MPI process, still with a single thread. To this end modify the job.sh script changing
#SBATCH --tasks-per-node=16
ncpu=`echo $nodes $nthreads 16 | awk '{print $1*$3/$2}'`
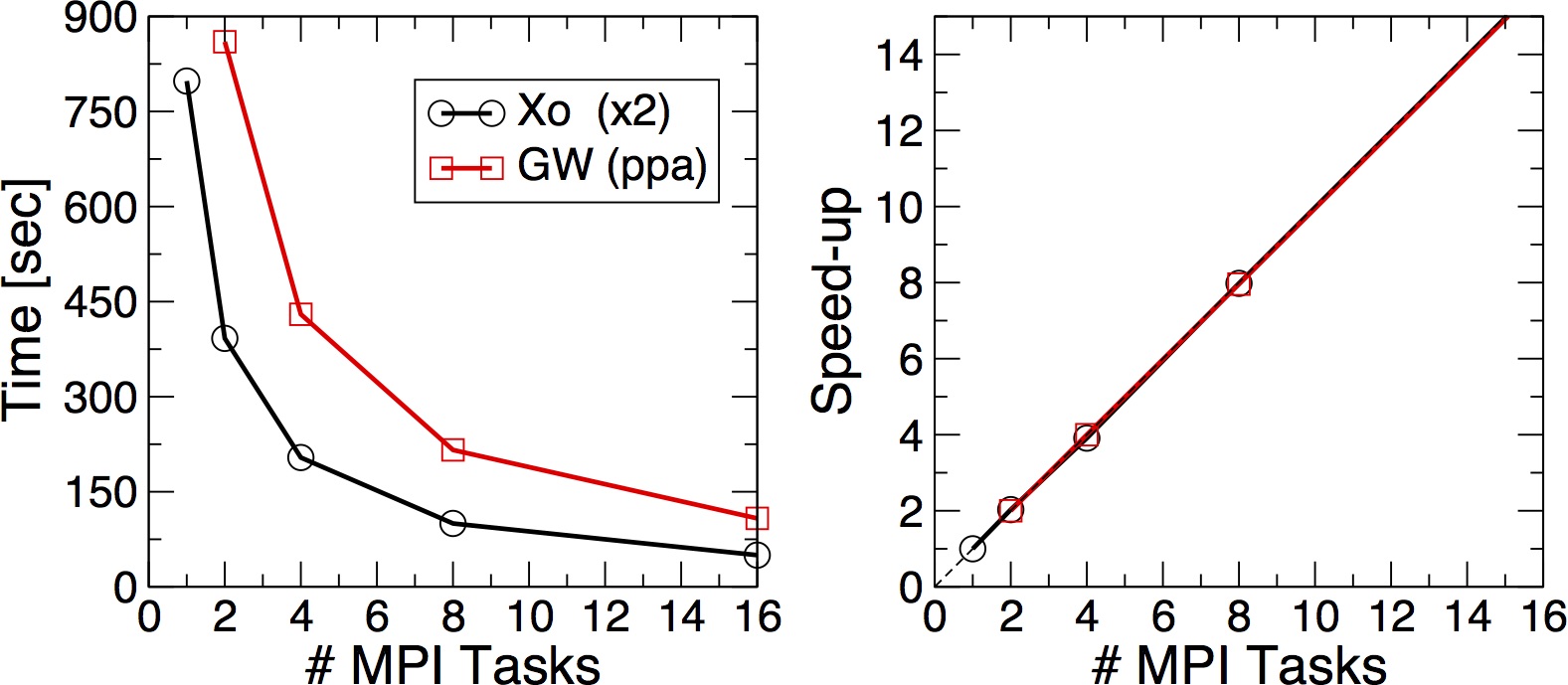
The two numbers (ncpu and tasks-per-node) must match. This time the code should be much faster. Once the run is over try to run the simulation also on 2, 4, 8. Each time please remember to change both the number of tasks per node and the number of CPUs. At the end you can try to produce a scaling plot.
To analyze the data you can use the phyton "yambo_parse.py" script which is also provided.
You can use it running
$ ./yambo_parse.py ${jobstring}/r-*
where $jobstring is the string you used for $jobname without the explicit number of MPI tasks.
You should obtain something like that (but with more columns)
# ncores MPI threads Dipoles Xo X Sgm_x Sgm_c WALL_TIME
1 1 1 1.00s 7m39.00s 0.00s 3.00s 1m46.00s 09m38s
2 2 1 2.00s 3m48.00s 0.00s 2.00s 53.00s 04m55s
4 4 1 0.00s 1m56.00s 0.00s 1.00s 27.00s 02m33s
8 8 1 0.00s 1m2.00s 0.00s 0.00s 14.00s 01m26s
16 16 1 0.00s 35.00s 0.00s 0.00s 7.00s 54s
Plot the execution time vs the number of MPI tasks and check (do a log plot) how far you are from the ideal linear scaling. Below a similar plot performed on Fermi
tips:
- not all runlevels scale in in the same way
- you should never overload the available number of cores
Pure OpenMP scaling
Next step is instead to check the OpenMP scaling. Set back
#SBATCH --tasks-per-node=16
and now use
nthreads=16 ncpu=`echo $nodes $nthreads 16 | awk '{print $1*$3/$2}'`
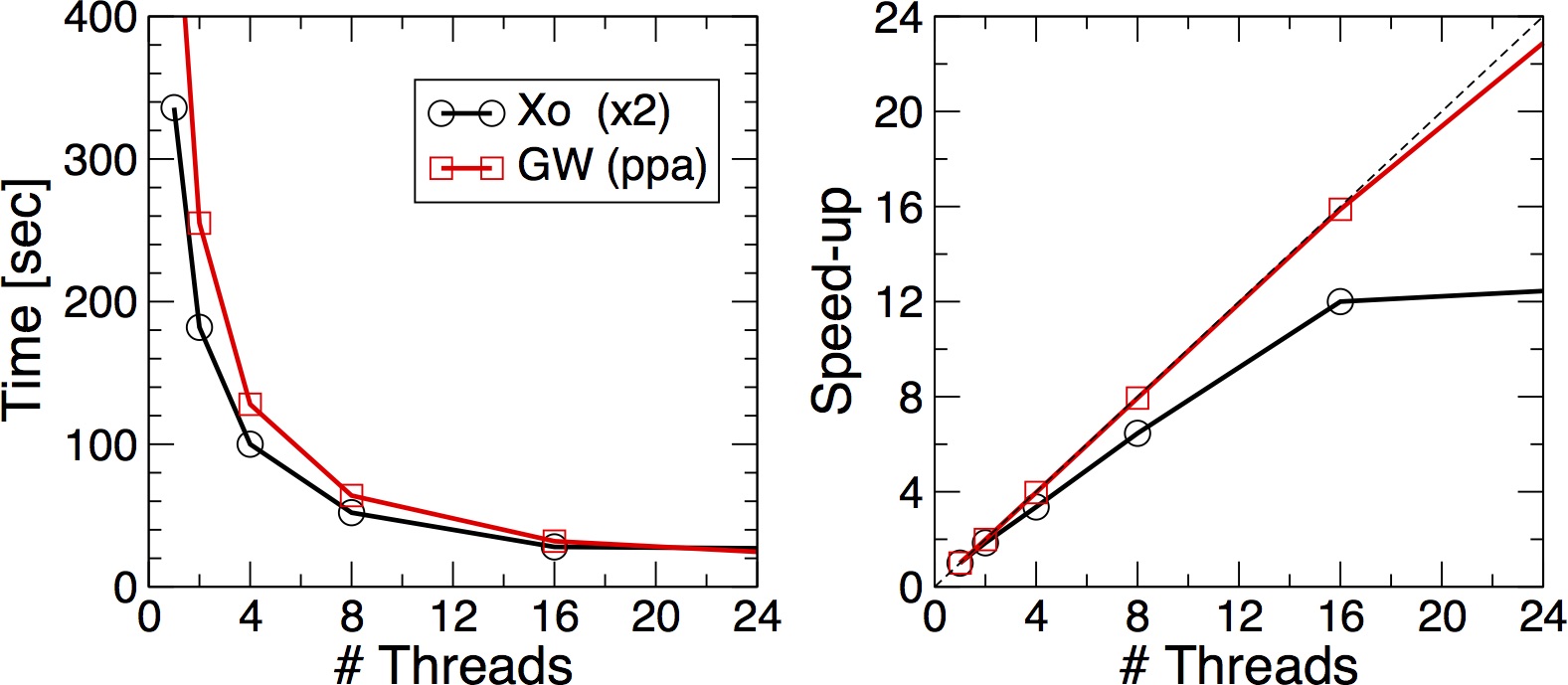
As before the nthreads and --tasks-per-node must match. Notice that here the last 16 entering the definition of "ncpu" defines the total number of cores (or better threads, see tips below). Since we are already using 16 threads, we cannot also split among MPI tasks, i.e. ncpu will result equal to 1. Try setting nthreads to 16, 8, 4 and 2 and again to plot the execution time vs the number of threads using the pyton script. Again you should be able to produce a plot similar to the following
tips:
- OpenMP usually shares the memory among threads, but not always
- you should never overload the available number of cores
- in principle we could overload the cores setting more threads than the available total number of cores, since a single core allows multi-thread operations
MPI vs OpenMP scaling
Which is scaling better ? MPI or OpenMP ? How is the memory distributed ?
Now you can try running simualations with hybrid strategies. Try for example setting:
#SBATCH --tasks-per-node=16 nthreads= 4 ncpu=`echo $nodes $nthreads 16 | awk '{print $1*$3/$2}'`
We can try to do scaling keeping the total number of tasks per node at 16. Parsing the data we will obtain something similar to
# ncores MPI threads Dipoles Xo X Sgm_x Sgm_c WALL_TIME
16 1 16 1.00s 38.00s 0.00s 2.00s 33.00s 01m25s
16 2 8 2.00s 34.00s 0.00s 1.00s 16.00s 01m06s
16 4 4 0.00s 34.00s 0.00s 1.00s 11.00s 56s
16 8 2 0.00s 33.00s 0.00s 0.00s 9.00s 52s
16 16 1 0.00s 35.00s 0.00s 0.00s 7.00s 54s
As you can see here the total CPU time decreases more and more moving the parallelization from the the OpenMP to the MPI level. Sigma_c in particular scales better. However the fastest run is not the one with 16 MPI task but the 8 2 configuration since Xo is faster using an hybrid MPI-OpenMP scheme.
However CPU time is not the only parameter you need to check. Also the total memory usage is important If you compare for example the two extreme cases (you can use)
$ grep Gb $jobname/l*_1 | grep Alloc (use this for the case with only one MPI proc) $ grep Gb $jobname/LOG/l*_1 | grep Alloc (use this for the case with more than one MPI proc)
For the case
# ncores MPI threads
16 1 16
<01s> [M 0.119 Gb] Alloc WF ( 0.112)
<03s> [M 0.314 Gb] Alloc WF ( 0.306)
<46s> [M 0.074 Gb] Alloc WF ( 0.056)
<50s> [M 0.321 Gb] Alloc WF ( 0.306)
the numbers reported above refer to the total amount of memory use in the run.
For the case
# ncores MPI threads
16 16 1
<02s> P0001: [M 0.034 Gb] Alloc WF ( 0.026)
<43s> P0001: [M 0.037 Gb] Alloc WF ( 0.019)
<45s> P0001: [M 0.091 Gb] Alloc WF ( 0.076)
the numbers reported above refer to the total amount of memory per MPI task. Multiplying by 16 you obtain an estimate of the total memory: 0.091*16=1.456 (0.076*16=1.216) These last two numbers have to be compared with 0.321 (0.306) As you can see yambo is distributing memory, since the single MPI task uses less memory than the total one needed (you can even compare with the serial case). However it is not as efficient as OpenMP in doing so.
Using an hybrid scheme you may also consider running yambo on mode than one node. To run on two nodes for example you need to set
#SBATCH -N 2 nodes=2
accordingly you can not set
nthreads= 4 ncpu=`echo $nodes $nthreads 32 | awk '{print $1*$3/$2}'`
This time you will use 32 cores with (16 per node) 4 OpenMP threads and 2*16/4=8 MPI tasks.
tips:
- in real life calculations running on n_cores > 100 it is a good idea to adopt an hybrid approach
- with OpenMP you cannot exit the single node, with MPI you can
Advanced: Comparing different parallelization schemes (optional)
Up to now we used the default parallelization scheme. Yambo also allows you to tune the parameters which controls the parallelization scheme. To this end you can open again the job.sh script and modify the section where the yambo input variables are set
X_all_q_CPU= "1 1 $ncpu 1" # [PARALLEL] CPUs for each role X_all_q_ROLEs= "q k c v" # [PARALLEL] CPUs roles (q,k,c,v) #X_all_q_nCPU_LinAlg_INV= $ncpu # [PARALLEL] CPUs for Linear Algebra X_Threads= 0 # [OPENMP/X] Number of threads for response functions DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles SE_CPU= "1 1 $ncpu" # [PARALLEL] CPUs for each role SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b) SE_Threads= 0
In particular "X_all_q_CPU" sets how the MPI Tasks are distributed in the calculation of the response function. The possibilities are shown in the "X_all_q_ROLEs". The same holds for "SE_CPU" and "SE_ROLEs" which control how MPI Tasks are distributed in the calculation of the response function.
Please try different parallelization schemes and check the performances of Yambo. In particular, also using the python script, you can chenck how speed, memory and load balance between the CPUs are affected. For more details see also the Parallel module
tips:
- the product of the numbers entering each variable (i.e. X_all_q_CPU and SE_CPU) times the number of threads should always match the total number of cores (unless you want to overload the cores taking advantage of multi-threads)
- using the X_Threads and SE_Threads variables you can think about setting different Hybrid schemes in between the screening and the self-energy runlevel.
- memory better scales if you parallelize on bands (c v b)
- parallelization on k-points performs similarly to parallelization on bands, but memory requires more memory
- parallelization on q-points requires much less communication in between the MPI tasks. It maybe useful if you run on more than one node and the inter-node connection is slow
| Prev: Tutorials Home | Now: Tutorials Home --> GW Parallel | Next: GW Convergence |