GW parallel strategies

In this tutorial we will see how to setup the variables governing the parallel execution of yambo in order to perform efficient calculations in terms of both cpu time and memory to solution. As a test case we will consider the hBN 2D material. Because of its reduced dimensionality, GW calculations turns out to be very delicate. Beside the usual convergence studies with respect to k-points and sums-over-bands, in low dimensional systems a sensible amount of vacuum is required in order to treat the system as isolated, translating into a large number of plane-waves. As for other tutorials, it is important to stress that this tutorial it is meant to illustrate the functionality of the key variables and to run in reasonable time, so it has not the purpose to reach the desired accuracy to reproduce experimental results. Moreover please also note that scaling performance illustrated below may be significantly dependent on the underlying parallel architecture. Nevertheless, general considerations are tentatively drawn in discussing the results.

Getting familiar with yambo in parallel

If you are not inside bellatrix, please follow the instructions in the tutorial home. If you are inside bellatrix and in the proper folder

[cecam.school01@bellatrix yambo_YOUR_NAME]$ pwd
/scratch/cecam.schoolXY/yambo_YOUR_NAME

you can proceed. First you need to obtain the appropriate tarball

$ cp /scratch/cecam.school/hBN-2D-para.tar.gz  ./  (Notice that this time there is not XY!)
$ tar -zxvf hBN-2D-para.tar.gz
$ ls
YAMBO_TUTORIALS
$ cd YAMBO_TUTORIALS/hBN-2D/YAMBO

To run a calculation on bellatrix you need to go via the queue system as explained in the Tutorials home. Under the YAMBO folder, together with the SAVE folder, you will see the run.sh script

$ ls
parse_yambo.py  run.sh  SAVE

First run the initialization as usual. Then you need to generate the input file for a GW run.

$ yambo -g n -p p -F yambo_gw.in 

The new input file should look like the folllowing. Please remove the lines you see below with a stroke and set the parameters to the same values as below

$ cat yambo_gw.in
#
#                                                           
# Y88b    /   e           e    e      888~~\    ,88~-_      
#  Y88b  /   d8b         d8b  d8b     888   |  d888   \     
#   Y88b/   /Y88b       d888bdY88b    888 _/  88888    |    
#    Y8Y   /  Y88b     / Y88Y Y888b   888  \  88888    |    
#     Y   /____Y88b   /   YY   Y888b  888   |  Y888   /     
#    /   /      Y88b /          Y888b 888__/    `88_-~      
#                                                           
#                                                           
#             GPL Version 4.1.2 Revision 120                
#                    MPI+OpenMP Build                       
#               http://www.yambo-code.org                   
#
ppa                          # [R Xp] Plasmon Pole Approximation
gw0                          # [R GW] GoWo Quasiparticle energy levels
HF_and_locXC                 # [R XX] Hartree-Fock Self-energy and Vxc
em1d                         # [R Xd] Dynamical Inverse Dielectric Matrix
X_Threads=  32               # [OPENMP/X] Number of threads for response functions 
DIP_Threads=  32             # [OPENMP/X] Number of threads for dipoles 
SE_Threads=  32              # [OPENMP/GW] Number of threads for self-energy 
EXXRLvcs= 21817        RL    # [XX] Exchange RL components
Chimod= ""                   # [X] IP/Hartree/ALDA/LRC/BSfxc
% BndsRnXp
    1 |  200 |               # [Xp] Polarization function bands
%
NGsBlkXp= 4            Ry    # [Xp] Response block size
% LongDrXp
 1.000000 | 0.000000 | 0.000000 |        # [Xp] [cc] Electric Field
%
PPAPntXp= 27.21138     eV    # [Xp] PPA imaginary energy
% GbndRnge
    1 |  200 |               # [GW] G[W] bands range
%
GDamping=  0.10000     eV    # [GW] G[W] damping
dScStep=  0.10000      eV    # [GW] Energy step to evaluate Z factors
DysSolver= "n"               # [GW] Dyson Equation solver ("n","s","g")
%QPkrange                    # [GW] QP generalized Kpoint/Band indices
  1| 1| 3| 6|
%

You can now open the submission script and the submission script

$ cat run.sh
 
#!/bin/bash
#SBATCH -N 1
#SBATCH -t 06:00:00 
#SBATCH -J test
#SBATCH --reservation=cecam_course
#SBATCH --tasks-per-node=1

nodes=1
nthreads=1
ncpu=`echo $nodes $nthreads 1 | awk '{print $1*$3/$2}'`

module purge
module load intel/16.0.3
module load intelmpi/5.1.3
bindir=/home/cecam.school/bin/

export OMP_NUM_THREADS=$nthreads

label=MPI${ncpu}_OMP${nthreads}
jdir=run_${label}
cdir=run_${label}.out

filein0=yambo_gw.in
filein=yambo_gw_${label}.in

cp -f $filein0 $filein
cat >> $filein << EOF
X_all_q_CPU= "1 1 $ncpu 1"  # [PARALLEL] CPUs for each role
X_all_q_ROLEs= "q k c v"    # [PARALLEL] CPUs roles (q,k,c,v)
X_all_q_nCPU_LinAlg_INV= $ncpu   # [PARALLEL] CPUs for Linear Algebra
X_Threads=  0               # [OPENMP/X] Number of threads for response functions
DIP_Threads=  0             # [OPENMP/X] Number of threads for dipoles
SE_CPU= " 1 1 $ncpu"        # [PARALLEL] CPUs for each role
SE_ROLEs= "q qp b"          # [PARALLEL] CPUs roles (q,qp,b)
SE_Threads=  0    

EOF

echo "Running on $ncpu MPI, $nthreads OpenMP threads"
srun -n $ncpu -c $nthreads $bindir/yambo -F $filein -J $jdir -C $cdir

As soon as you are ready submit the job.

$ sbatch run.sh

Yambo calculates the GW-qp corrections running on 1 MPI process with a single thread. As you can see, monitoring the log file produced by yambo, the run takes some time, although we are using minimal parameters.

Pure MPI scaling with default parallelization scheme

Meanwhile we can run the code in parallel. Let's use 16 MPI process, still with a single thread. To this end modify the job.sh script changing

#SBATCH --tasks-per-node=16

ncpu=`echo $nodes $nthreads 16 | awk '{print $1*$3/$2}'`

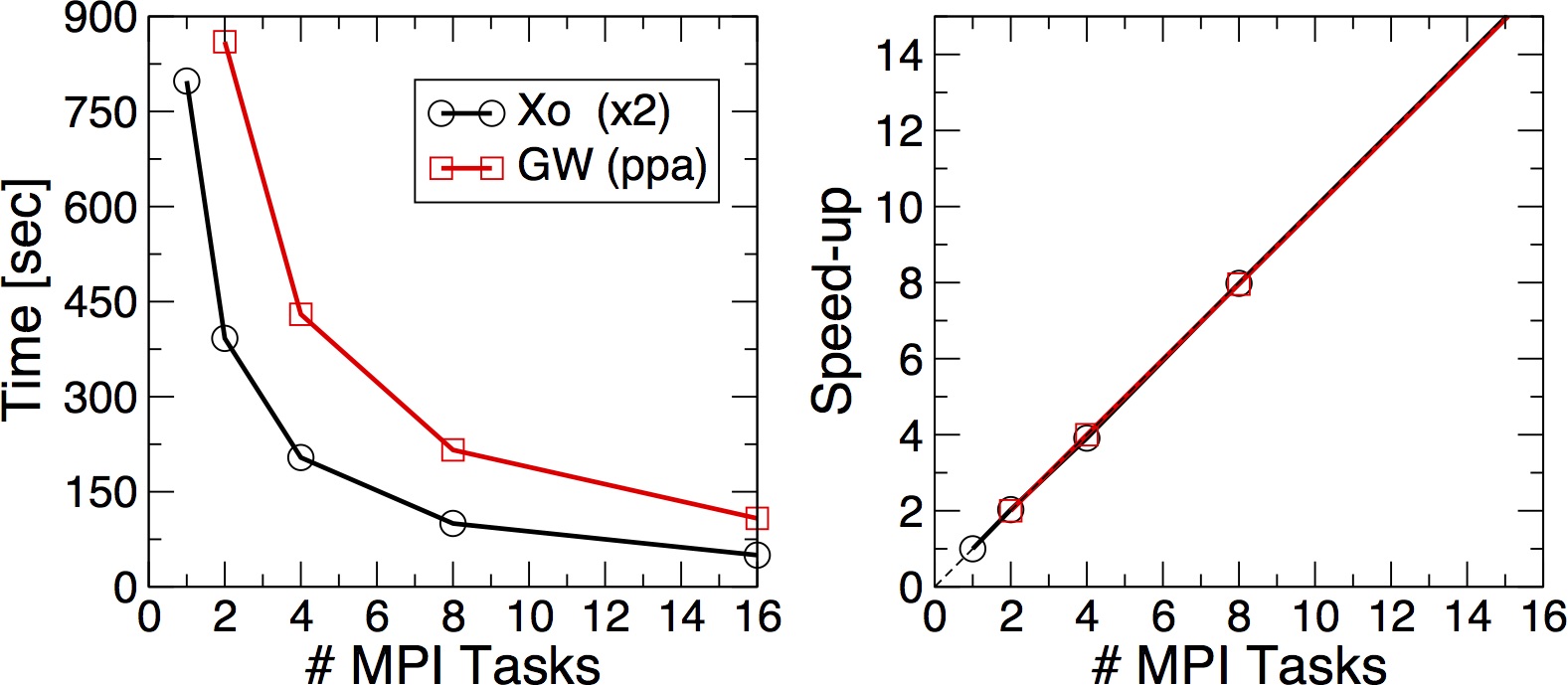
The two numbers (ncpu and tasks-per-node) must match. This time the code should be much faster. Once the run is over try to run the simulation also on 2, 4, 8. Each time please remember to change both the number of tasks per node and the number of CPUs. At the end you can try to produce a scaling plot.

To analyze the data you can use the phyton "yambo_parse.py" script which is also provided.

You can use it running

$ ./yambo_parse.py ${jobstring}/r-*

where $jobstring is the string you used for $jobname without the explicit number of MPI tasks.

You should obtain something like that (but with more columns)

# ncores         MPI     threads     Dipoles          Xo           X       Sgm_x       Sgm_c   WALL_TIME
      1           1           1       1.00s    7m39.00s       0.00s       3.00s    1m46.00s      09m38s
      2           2           1       2.00s    3m48.00s       0.00s       2.00s      53.00s      04m55s
      4           4           1       0.00s    1m56.00s       0.00s       1.00s      27.00s      02m33s
      8           8           1       0.00s     1m2.00s       0.00s       0.00s      14.00s      01m26s
     16          16           1       0.00s      35.00s       0.00s       0.00s       7.00s         54s

Plot the execution time vs the number of MPI tasks and check (do a log plot) how far you are from the ideal linear scaling. Below a similar plot performed on Fermi

Advanced: Comparing different parallelization schemes (optional)

Up to now we used the default parallelization scheme. To change this you can open again the job.sh script and modify the section where the yambo input variables are set

X_all_q_CPU= "1 1 $ncpu 1"   # [PARALLEL] CPUs for each role
X_all_q_ROLEs= "q k c v"     # [PARALLEL] CPUs roles (q,k,c,v)
#X_all_q_nCPU_LinAlg_INV= $ncpu   # [PARALLEL] CPUs for Linear Algebra
X_Threads=  0               # [OPENMP/X] Number of threads for response functions
DIP_Threads=  0             # [OPENMP/X] Number of threads for dipoles
SE_CPU= "1 1 $ncpu"             # [PARALLEL] CPUs for each role
SE_ROLEs= "q qp b"               # [PARALLEL] CPUs roles (q,qp,b)
SE_Threads=  0    

In particular "X_all_q_CPU" sets how the MPI Tasks are distributed in the calculation of the parallelization. The possibilities are shown in the "X_all_q_ROLEs"

Pure OpenMP scaling

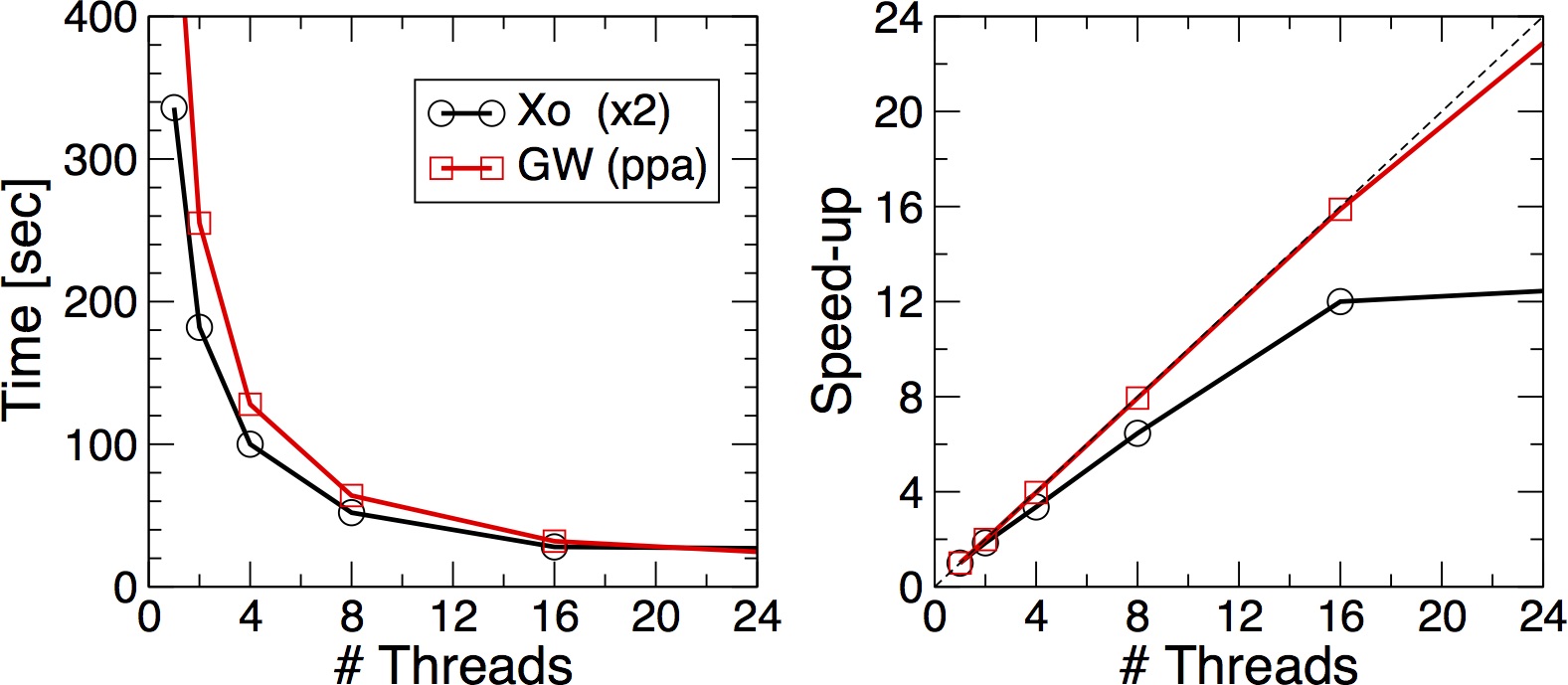
Next step is instead to check the OpenMP scaling. Set back

#SBATCH --tasks-per-node=16

and now use

nthreads=16
ncpu=`echo $nodes $nthreads 1 | awk '{print $1*$3/$2}'`

As before the nthreads and --tasks-per-node must match. Try setting nthreads to 16, 8, 4 and 2 and again to plot the execution time vs the number of threads using the pyton script. Again you should be able to produce a plot similar to the following

MPI vs OpenMP scaling

Which is scaling better ? MPI or OpenMP ? How is the memory distributed ?

Now you can try running simualations with hybrid strategies. Try for example setting:

#SBATCH --tasks-per-node=16

nthreads= 4
ncpu=`echo $nodes $nthreads 4 | awk '{print $1*$3/$2}'`

We can try to do scaling keeping the total number of tasks per node at 16. Parsing the data we will obtain something similar to

 # ncores         MPI     threads     Dipoles       Xo           X       Sgm_x       Sgm_c   WALL_TIME
     16           1          16       1.00s      38.00s       0.00s       2.00s      33.00s      01m25s
     16           2           8       2.00s      34.00s       0.00s       1.00s      16.00s      01m06s
     16           4           4       0.00s      34.00s       0.00s       1.00s      11.00s         56s
     16           8           2       0.00s      33.00s       0.00s       0.00s       9.00s         52s
     16          16           1       0.00s      35.00s       0.00s       0.00s       7.00s         54s

As you can see here the total CPU time decreases more and more moving the parallelization from the the OpenMP to the MPI level. Sigma_c in particular scales better. However the fastest run is not the one with 16 MPI task but the 8 2 configuration since Xo is faster using an hybrid MPI-OpenMP scheme.