Real time Bethe-Salpeter Equation (density matrix only)
Introduction
This tutorial will show how to perform a real-time calculation with Yambo on hBN monolayer. We will go through different approximations for the many body self--energy (HXC potential in the yambo language) up to the HSEX approximation which captures the physics of the exciton. For approximations local in space, like "TD-HARTREE" and "TD-DFT", the HXC potential can be evaluated directly during the simulation from real space quantities. On the contrary for approximations non local in space, one first needs to compute the "real time collisions".
The same DFT inputs used to generate the hBN-2D-RT.tar.gz, are sufficient to converge the energy of the first exciton. You will need to increase the number of k-points to converge higher energy excitons.
TD Hartree and TD DFT
Let us start by going to the previous folder where we ran the real-time initialization and the tutorial on linear response:
cd YAMBO_TUTORIALS/hBN-2D-RT/YAMBO/FixSymm
TD Hartree
yambo_rt -n p -v hartree -F Inputs_rt/02_td_hartree.in
negf # [R] Real-Time dynamics HXC_Potential= "HARTREE" # [SC] SC HXC Potential HARRLvcs= 1000 mHa # [HA] Hartree RL components VXCRLvcs= 0. mHa # [HA] DFT RL components % RTBands 3 | 5 | # [RT] Bands % Integrator= "RK2" # [RT] Integrator. Use keywords space separated ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA") PhLifeTime= 100.0000 fs # [RT] Dephasing Time RTstep=10.000000 as # [RT] Real Time step length NETime= 20.00000 fs # [RT] Simulation Time % IOtime 0.01 | 1.00 | 0.01 | fs # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT) % % Field1_Freq 0.00 | 0.00 | eV # [RT Field1] Frequency % Field1_Int= 1.E3 kWLm2 # [RT Field1] Intensity Field1_Width= 0.000000 fs # [RT Field1] Width Field1_kind= "DELTA" # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) Field1_pol= "linear" # [RT Field1] Pol(linear|circular) % Field1_Dir 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor % % Field1_Tstart= 0.000000fs # [RT Field1] Initial Time
We set the cut-off on the Hartree potential to 1000 mHa. This defines the cutoff used to evaluate the Hartree potential at each time step. Notice also the need of setting the cutoff to Vxc to zero. This time we will propagate for just 20 fs. It is useful to run the simulation in background and then monitor the output file
nohup yambo_rt -F Inputs_rt/02_td_hartree.in -J TD-HARTREE_1000mHa -C TD-HARTREE_1000mHa & tail -f TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization
We can even have check the output on the fly.
To interrupt tail -f
ctrl+C
Then
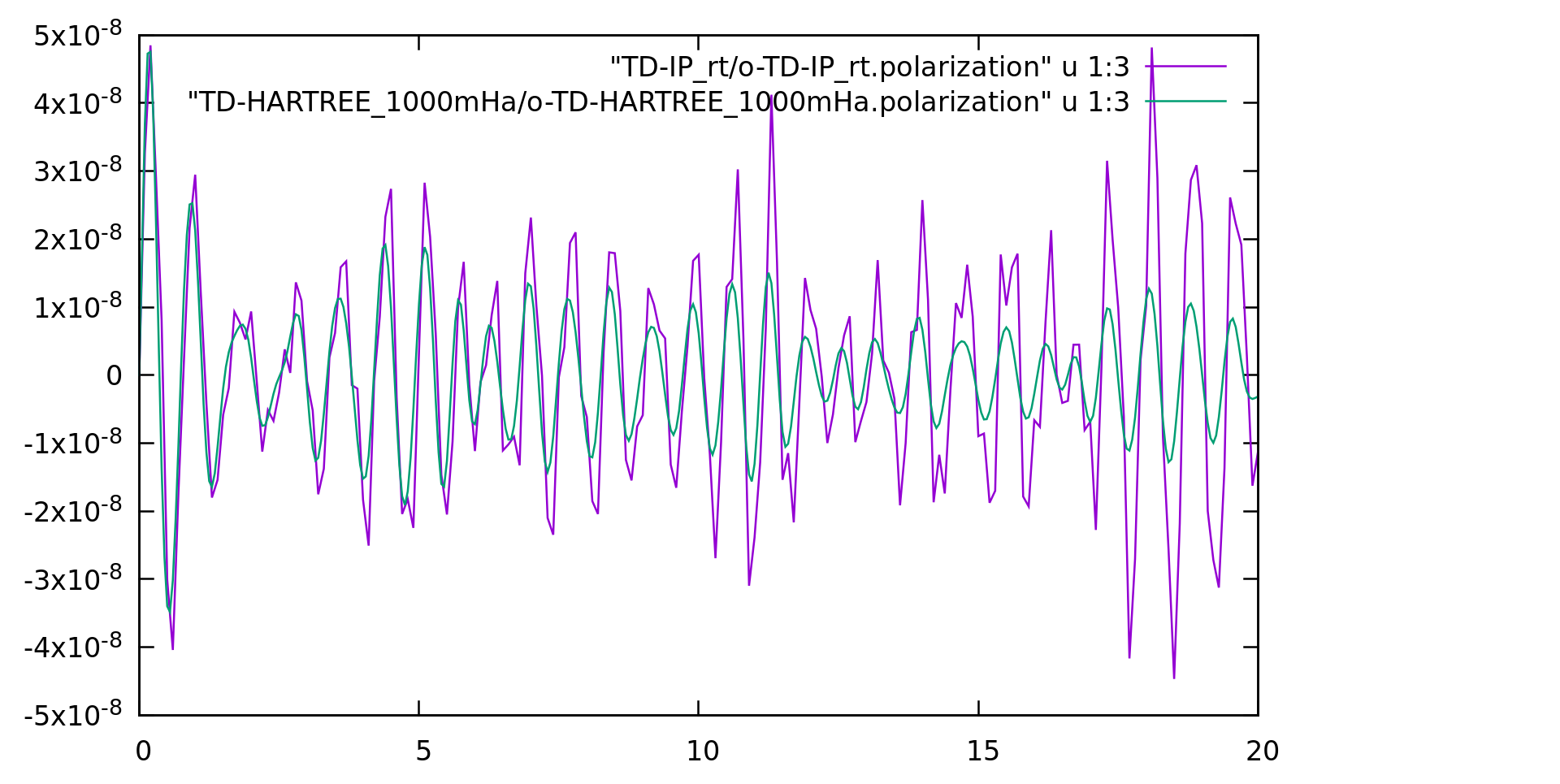
gnuplot set xrange [0:20] plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l,"TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization" u 1:3 w l
We can already see from the output that the polarization is not very different from the IP one.
The major difference is indeed due to the presence of a damping (or dephasing term) in the output (PhLifeTime, i.e. the life-time of the phase).
If we check the timing of the simulation we see that most of the time is spent in the following subroutines:
el_density_matrix : 7.5074 s CPU ( 4002 calls, 0.0019 s avg)
V_Hartree : 1.0405 s CPU ( 4002 calls, 0.0003 s avg)
V_real_space_to_H : 23.8210 s CPU ( 220220 calls, 0.0001 s avg)
RT Hamiltonian : 32.5007 s CPU ( 4001 calls, 0.0081 s avg)
The evaluation of the Hartree potential by itself does not take too much time. It is more consuming to evaluate the real space density. However it is the projection of the potential into the transition space (V_real_space_to_H) which takes most of the time. RT_Hamiltonian is just (roughly) the sum of the two previous subroutines. You can see how these timings change if you increase the cutoff on the Hartree potential.
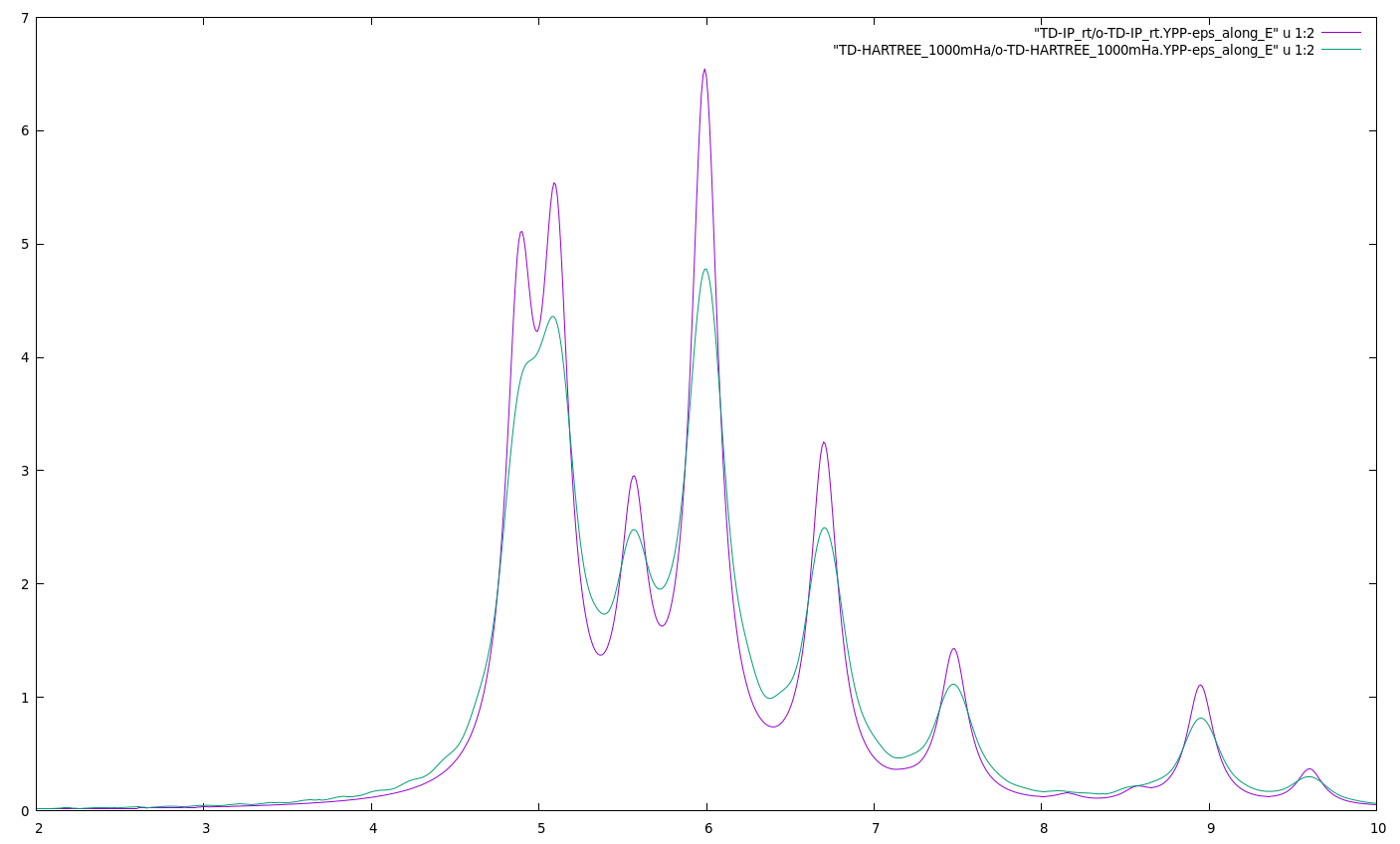
Thus we can expect that also the absorption will be quite similar. Indeed hBN is uniform in the plane and so the local-field effects should be small.
As previously you can now do a post-processing of the polarization. The input file is exactly the same
ypp_rt -F Inputs_rt/ypp_abs.in -J TD-HARTREE_1000mHa -C TD-HARTREE_1000mHa gnuplot set xrange [2:10] plot "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l, "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l
The situation would be completely different if we computed the polarization out of plane at both the TD-IP and the TD-Hartree level. You can try if you wish, but remember that you have to go back to the original SAVE folder and remove the symmetries not consistent with a field along the z direction this time: (see Prerequisites))
TD DFT
You can now try to perform a TDDFT simulation. Let's use the previous input file
cp Inputs_rt/02_td_hartree.in Inputs_rt/03_td_dft.in
and modify it
vim Inputs_rt/03_td_dft.in
negf # [R] Real-Time dynamics HXC_Potential= "HARTREE+GS_XC" # [SC] SC HXC Potential HARRLvcs= 1.E3 mHa # [HA] Hartree RL components VXCRLvcs= 1.E3 mHa
We can now run the TD-DFT simulation
nohup yambo_rt -F Inputs_rt/03_td_dft.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA & tail -f TD-DFT_1000mHA/o-TD-DFT_1000mHA.polarization
and once it is over do the post processing
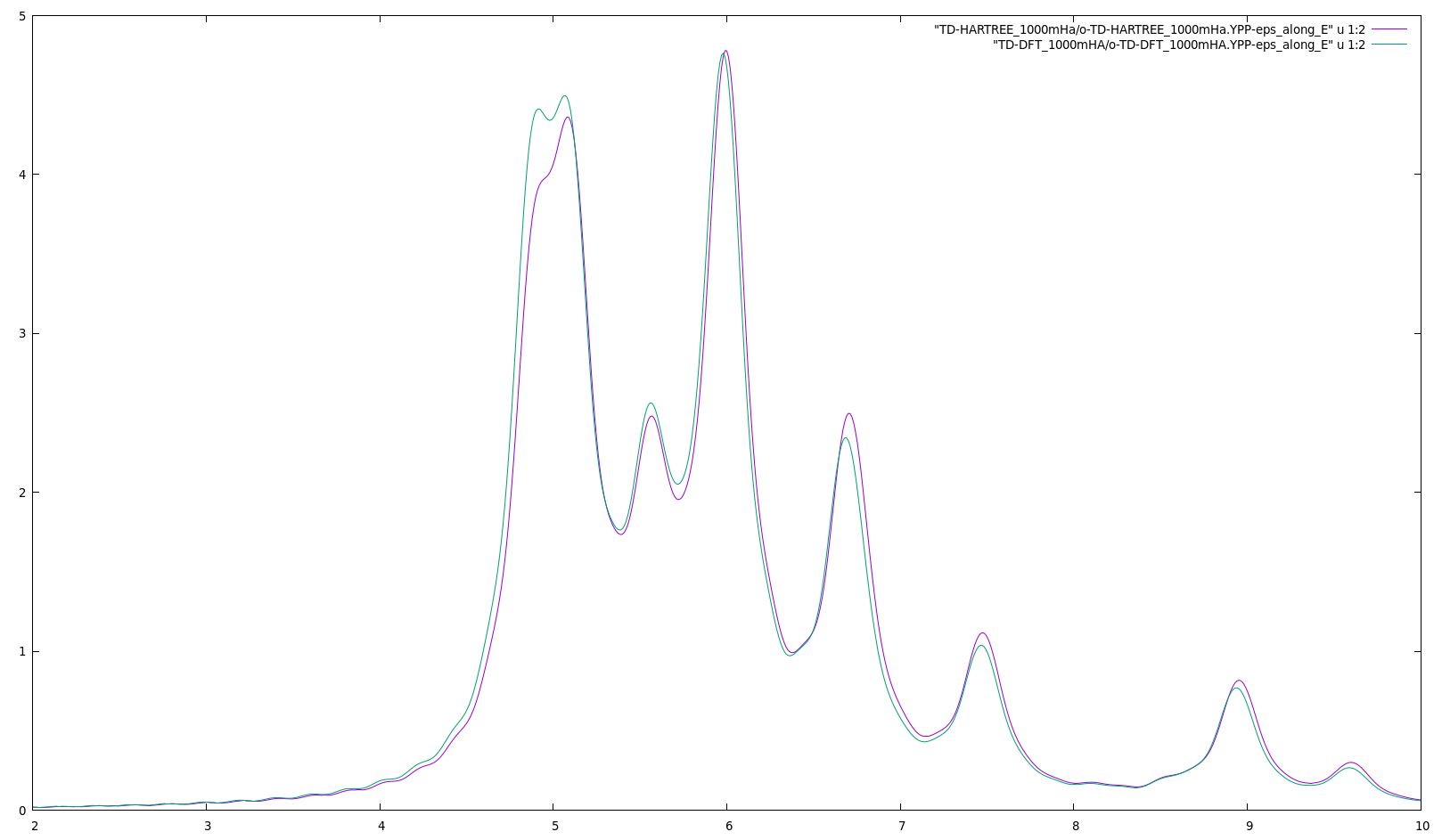
ctrl+C ypp_rt -F Inputs_rt/ypp_abs.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA gnuplot plot "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l,"TD-DFT_1000mHA/o-TD-DFT_1000mHA.YPP-eps_along_E" u 1:2 w l
As expected TDDFT does not improve much over TD-HARTREE in extended systems
The Real Time Collisions
We next move to the evaluation of the collisions (see Introduction to Real Time propagation in Yambo to recall what the collisions are).
This part is common between yambo_nl and yambo_rt.
Generate the input file to calculate the collisions (see appendix of Ref. [1]) using the command:
yambo_rt -X s -e -v hsex -F Inputs_rt/03_coll_hsex.in
The flag -X will tell the code to calculate the dielectric constant that is required for the screened interaction.
It could be even computed in an independent calculation and then loaded using the -J flags
em1s # [R Xs] Static Inverse Dielectric Matrix
dipoles # [R ] Compute the dipoles
Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% BndsRnXs
1 | 20 | # [Xs] Polarization function bands
%
NGsBlkXs= 1000 mHa # [Xs] Response block size
% DmRngeXs
0.10000 | 0.10000 | eV # [Xs] Damping range
%
% LongDrXs
1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field
%
While this is the part of the input file specific for the evaluation of the collisions
collisions # [R] Eval the extended Collisions % COLLBands 4 | 5 | # [COLL] Bands for the collisions % HXC_Potential= "HARTREE+SEX" # [SC] SC HXC Potential HARRLvcs= 1000 mHa # [HA] Hartree RL components EXXRLvcs= 1000 mHa # [XX] Exchange RL components CORRLvcs= 1000 mHa # [GW] Correlation RL components
With this input, we calculate the HARTREE plus SEX collisions integrals. Notice that the HARTREE term in principle can be calculated on the fly, but in this way it is more efficient especially for the non-linear response.
Here one has to converge the cutoff for the Hartree and the Screened Exchange. Around 5000 mHa is a reasonable value for hBN. In this example we will use 1000 mHa to speed up calculations. The collisions bands COLLBands have to be the same number of bands you want to use in the linear/nonlinear response.
The you can run
yambo_rt -F Inputs_rt/03_coll_hsex.in -J COLL_HSEX -C COLL_HSEX
The calculation will take about 1 minute in serial.
It produced many binary files ndb.COLLISIONS_HXC_fragment_* which will be needed to perform TD-HSEX simulations.
Notice that, if you want, you can also compute simple HARTREE collisions and use them in a TD-HARTREE simulation.
TD-HARTREE with collisions (optional)
Then generate the input file to calculate the collisions (see appendix of Ref. [1]) use the command :
yambo_rt -e -v h -F Inputs_rt/03_coll_hartree.in
with a simpler input file
collisions # [R] Eval the extended Collisions % COLLBands 4 | 5 | # [COLL] Bands for the collisions % HXC_Potential= "HARTREE" # [SC] SC HXC Potential HARRLvcs= 1000 mHa # [HA] Hartree RL components
yambo_rt -F Inputs_rt/03_coll_hartree.in -J COLL_HARTREE -C COLL_HARTREE yambo_rt -F Inputs_rt/02_td_hartree.in -J "TD-HARTREE_COLL,COLL_HARTREE" -C TD-HARTREE_COLL
and compare the run with the simulation without collision. One major difference, is that, when the collisions are used, yambo does not need to load the wave--function anymore and the simulation is much faster. The drawback is that for big systems the folder COLL_HARTREE may become huge, thus requiring a lot of disk space.
Time dependent Bethe Salpeter equation
To generate the input for the real-time simulation you can run
yambo_rt -n p -v hsex -V qp -F Inputs_rt/04_td_hsex.in
As you can see this time the extra verbosity for quasi-particles is used -V qp
The reason is that, to be consistent with the TD-HSEX, simulation we need to apply quasi-particles corrections.
The input file is
negf # [R] NEQ Real-time dynamics HXC_Potential= "SEX+HARTREE" # [SC] SC HXC Potential % RTBands 4 | 5 | # [RT] Bands % Integrator= "RK2" # [RT] Integrator. Use keywords space separated ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA") PhLifeTime= 100.0000 fs # [RT] Dephasing Time RTstep=10.000000 as # [RT] Real Time step length NETime= 30.00000 fs # [RT] Simulation Time % IOtime 0.01 | 1.00 | 0.05 | fs # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT) % HARRLvcs= 1000 mHa # [HA] Hartree RL components EXXRLvcs= 1000 mHa # [XX] Exchange RL components CORRLvcs= 1000 mHa # [GW] Correlation RL components
% GfnQP_E
3.000000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim
%
% Field1_Freq 0.00 | 0.00 | eV # [RT Field1] Frequency % Field1_Int= 1.E3 kWLm2 # [RT Field1] Intensity Field1_Width= 0.000000 fs # [RT Field1] Width Field1_kind= "DELTA" # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) Field1_pol= "linear" # [RT Field1] Pol(linear|circular) % Field1_Dir 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor % % Field1_Dir_circ 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor_circ % Field1_Tstart= 0.000000fs # [RT Field1] Initial Time
and then run the code. Notice the presence of the COLL_HSEX among the options after -J
nohup yambo_rt -F Inputs_rt/04_td_hsex.in -J "TD-SEX_rt,COLL_HSEX" -C TD-SEX_rt &
Final post processing
Now you can analyze the response with
ypp_rt -F Inputs_rt/ypp_abs.in -J TD-SEX_rt -C TD-SEX_rt
as it was done the linear response tutorial and compare with the TD-IP run (and possibly against the standard Bethe-Salpeter):
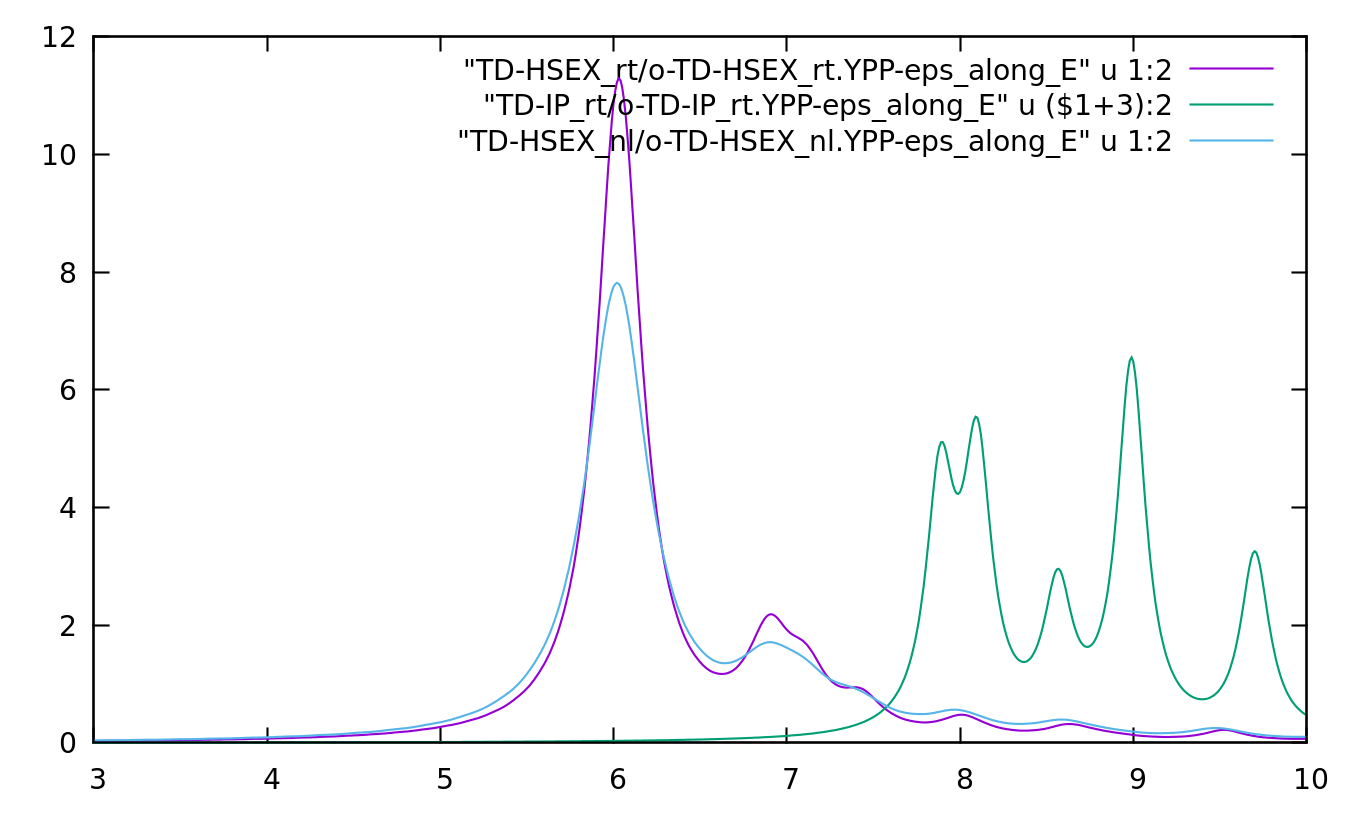
gnuplot> set xrange [3:10] gnuplot> set yrange [0:12] gnuplot> plot "TD-SEX_rt/o-TD-SEX_rt.YPP-eps_along_E" u 1:2 w l, "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u ($1+3):2 w l
Linear response results can be obtained following the BSE tutorial. Notice that you can use the SEX approximation for the non-linear response too (see the following tutorials on non-linear response).
References
Links
- Back to Rome 2023#Tutorials