Modena 2025 : Yambopy part 1
The first section of this tutorial will show you how to visualise wave-function and band-structure related information, such as atomic, orbital and spin projections, following a DFT Quantum Espresso calculation using the "qepy" submodule of Yambopy. In the second section, we will start using the "yambopy" submodule to read the Yambo binary databases in order access reciprocal space data, dipole matrix elements and the RPA response function.
In order to run both parts 1 and 2, you need to copy and extract the tar file named yambopy_tutorial_Modena_2025.tar.gz that you find in the WORK directory:
cd $SCRATCH mkdir -p YAMBOPY_TUTORIALS cd YAMBOPY_TUTORIALS rsync -avzP /leonardo_work/tra25_yambo/YAMBOPY_TUTORIALS/yambopy_tutorial_Modena_2025.tar.gz . tar --strip-components=1 -xvzf yambopy_tutorial_Modena_2025.tar.gz
Plot band structures from Quantum ESPRESSO
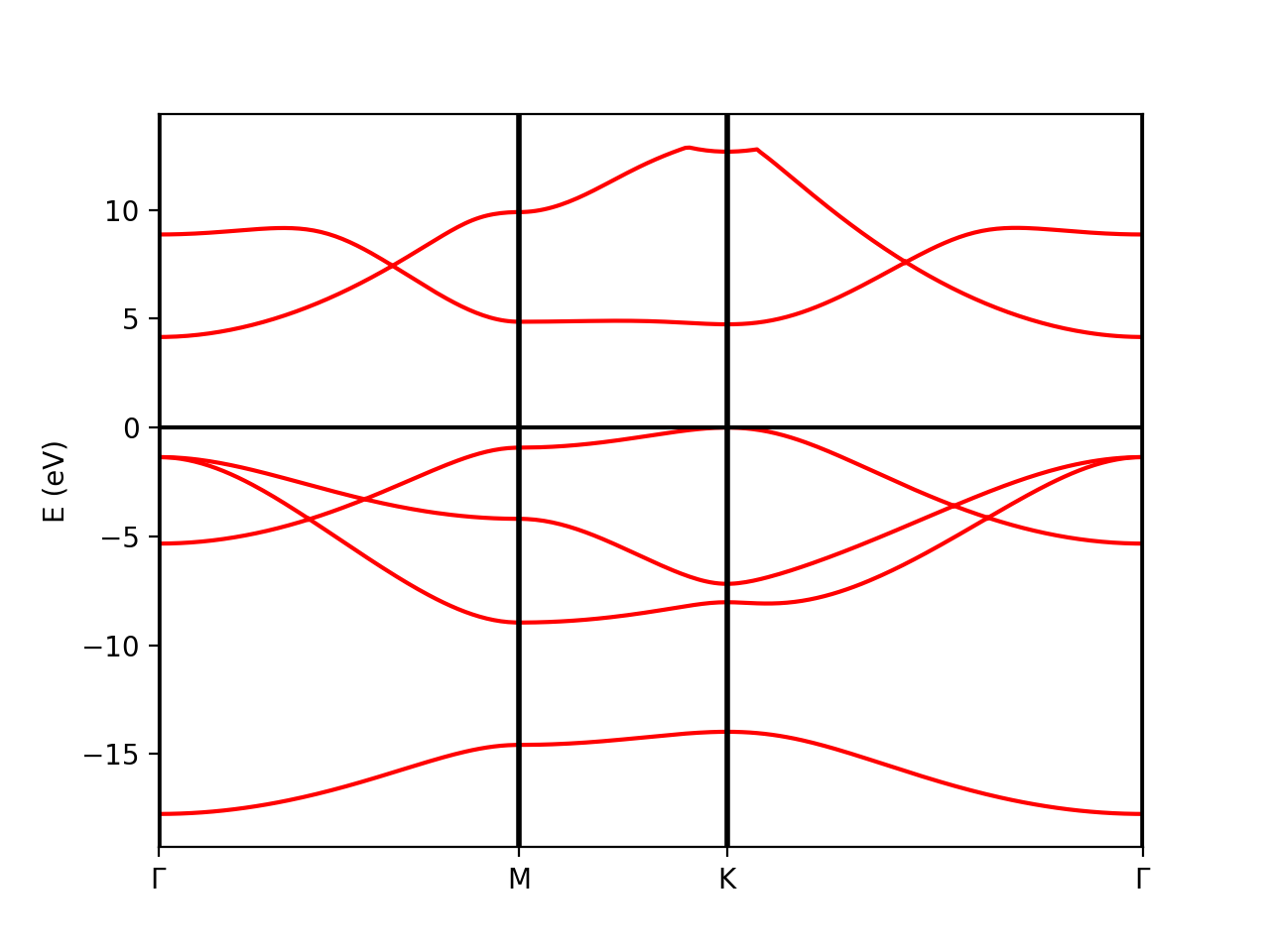
Tutorial 1. BN (semiconductor). Band structure
First enter in the folder
cd databases_qepy/bn-semiconductor
and have a look to the
vim plot-qe-bands.py
The qepy classes are useful both to execute Quantum Espresso and to analyze the results. Enter in the python environment, by typing python, then the full qepy library is imported by simply doing:
from qepy import *
Plot Band structure
The qepy class PwXML reads the data file generated by Quantum Espresso and post-processes the data. The class is instanced by doing:
xml = PwXML(prefix='bn', path='bands')
The variable prefix corresponds to the same variable of the QE input. The folder location is indicated by variable path. In order to plot the bands, we also define the k-points path (in crystal coordinates) using the function Path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0],'$\Gamma$'],
[[0.5, 0.0, 0.0],'M'],
[[1./3,1./3,0.0],'K'],
[[0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)])
It is worth to note that the path should coincide with the selected path for the QE band calculations.
In order to show the plot we can call the plot_eigen method of the PwXML class:
xml.plot_eigen(path_kpoints)
This function will automatically plot the bands. Alternatively, we can use the function plot_eigen_ax:
fig = plt.figure() ax = fig.add_subplot(1,1,1) xml.plot_eigen_ax(ax,path_kpoints)
This functions requires as input a matplotlib figure object with given axes. We can produce a figure by running the script:
python plot-qe-bands.py
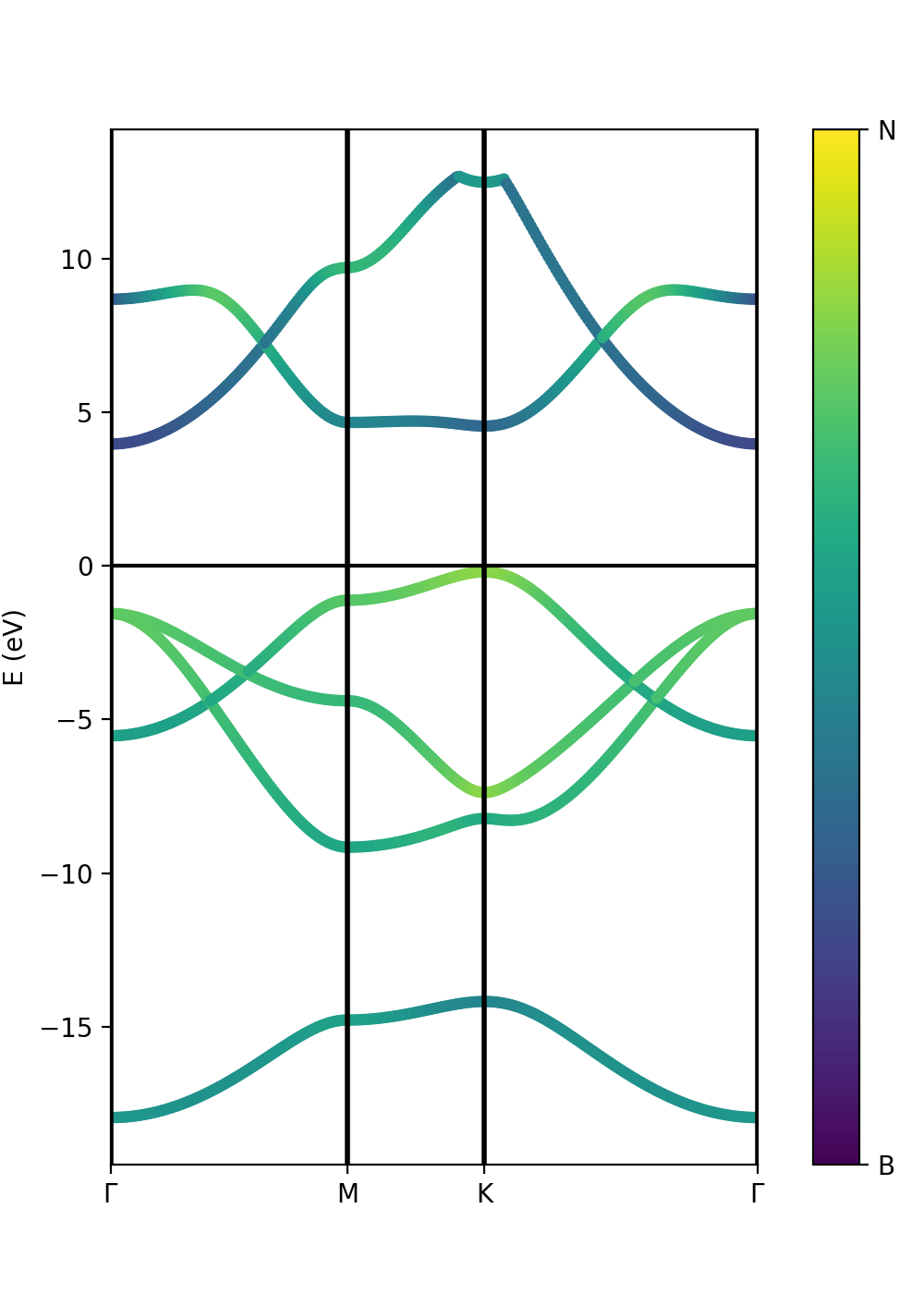
Plot atomic orbital projected Band structure
In addition to the band structure, useful information regarding the atomic orbital nature of the electronic wave functions can be displayed using the class ProjwfcXML. In order to make quantum espresso calculate the relevant data, we need to use the QE executable projwfc.x, which will create the file atomic_proj.xml. This executable projects the Kohn-Sham wavefunctions onto orthogonalized atomic orbitals, among others functionalities. The orbital indexing and ordering are explained in the input documentation of the projwfc.x function which you are invited to check (https://www.quantum-espresso.org/Doc/INPUT_PROJWFC.html#idm94). In this example, projwfc.x has been already run.
As in the class PwXML, we then define the path_kpoints and also the selected atomic orbitals to project our bands. We have chosen to represent the projection weight onto the nitrogen (1) and boron (2) orbitals, which can be obtained with
# Automatic selection of the states atom_1 = band.get_states_helper(atom_query=['N']) atom_2 = band.get_states_helper(atom_query=['B'])
The full list of orbitals is written in the file bands/prowfc.log. By inspecting it, you may also construct custom lists of states.
We have also defined the figure box
import matplotlib.pyplot as plt fig = plt.figure(figsize=(5,7)) ax = fig.add_axes( [ 0.12, 0.10, 0.70, 0.80 ])
The class ProjwfcXML then runs as in this example:
band = ProjwfcXML(prefix='bn',path='bands',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',selected_orbitals=atom_1,selected_orbitals_2=atom_2)
We can run now the file:
python plot-qe-orbitals.py
We have chosen the colormap 'viridis' (variable cmap). You see that the colormap goes from maximum selected_orbitals content (in this case nitrogen) to the maximum selected_orbitals_2 content (in this case boron). The colormap can be represented in many ways and qepy does not include a particular function for this. An example is:
import matplotlib as mpl
cmap=plt.get_cmap('viridis')
bx = fig.add_axes( [ 0.88, 0.10, 0.05, 0.80 ])
norm = mpl.colors.Normalize(vmin=0.,vmax=1.)
cb1 = mpl.colorbar.ColorbarBase(bx, cmap=cmap, norm=norm,orientation='vertical',ticks=[0,1])
cb1.set_ticklabels(['B', 'N'])
Suppose now that we have run a G0W0 calculation (see part 2 of the Yambopy tutorial), and we want to represent the atomic weights on top of the quasiparticle band structure instead of the Kohn-Sham one. However, we do not have the same kpoint grid between the G0W0 calculation and the quantum espresso "band" calculation along a path. We can then extract the parameters for a scissor operator (this is done in part 2) and feed them to the ProjwfcXML class together with the number of valence bands. Try uncommenting the following lines in the tutorial script:
# Add scissor operator to the bands from a G0W0 calculation scissor= [1.8985195950522469, 1.0265240811345133, 1.051588659878575] n_val = 4 band.add_scissor(n_val,scissor)
Finally, we can also plot the band orbital character with size variation instead of a color scale. In this case we have to pass only the variable selected_orbitals (see below).
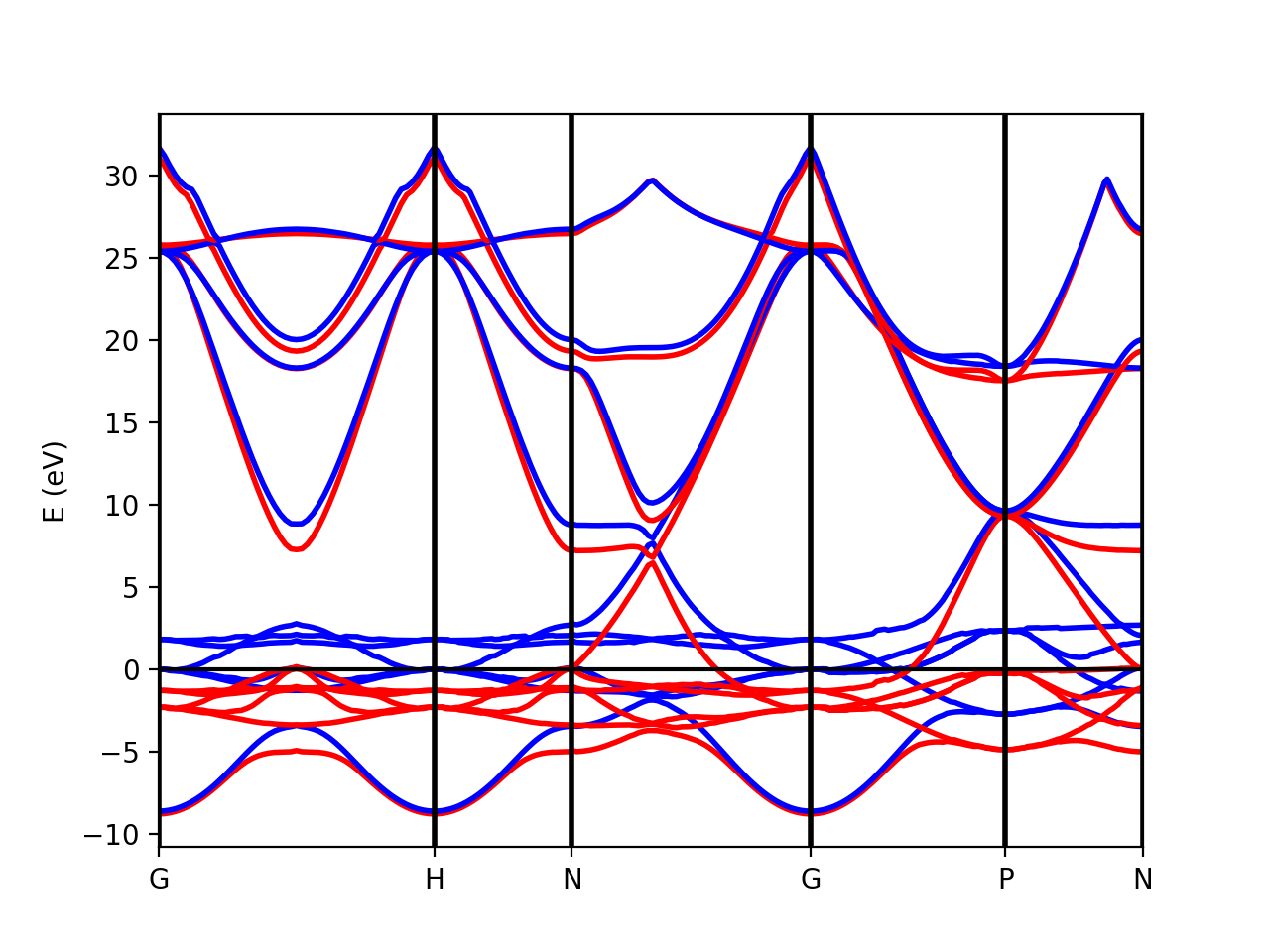
Tutorial 2. Iron. Ferromagnetic metallic material
Let's move to a magnetic system:
cd ../iron-metal
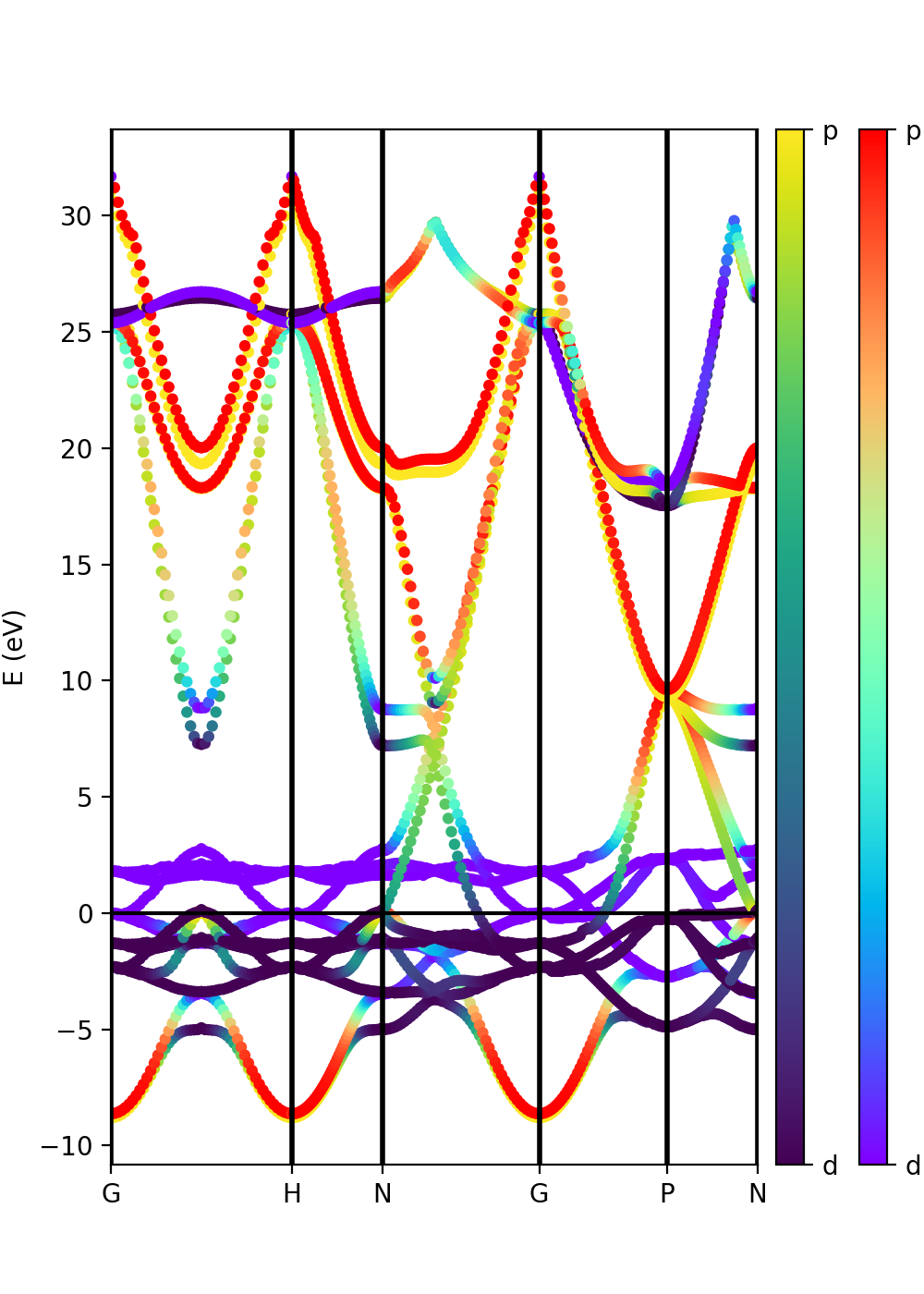
In the case of spin-polarized calculations we can plot the spin up and down band structures. After completing a band structure calculation for iron with Quantum ESPRESSO, we can make the band plot by running the script:
python plot-qe-bands.py
The class PwXML automatically detects the spin polarized case (nspin=2 in the QE input file). The spin up channel is displayed with red and the spin down channel with blue. In the case of iron we have selected this k-point path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0 ],'G'],
[[0.0, 0.0, 1.0 ],'H'],
[[1./2,0.0,1./2.],'N'],
[[0.0, 0.0, 0.0 ],'G'],
[[1./2, 1./2, 1./2 ],'P'],
[[1./2,0.0,1./2. ],'N']], [npoints,npoints,npoints,npoints,npoints])
xml = PwXML(prefix='pw',path='bands/t0') #xml.plot_eigen(path_kpoints) fig = plt.figure() ax = fig.add_subplot(1,1,1) xml.plot_eigen_ax(ax,path_kpoints,lw=1.5)
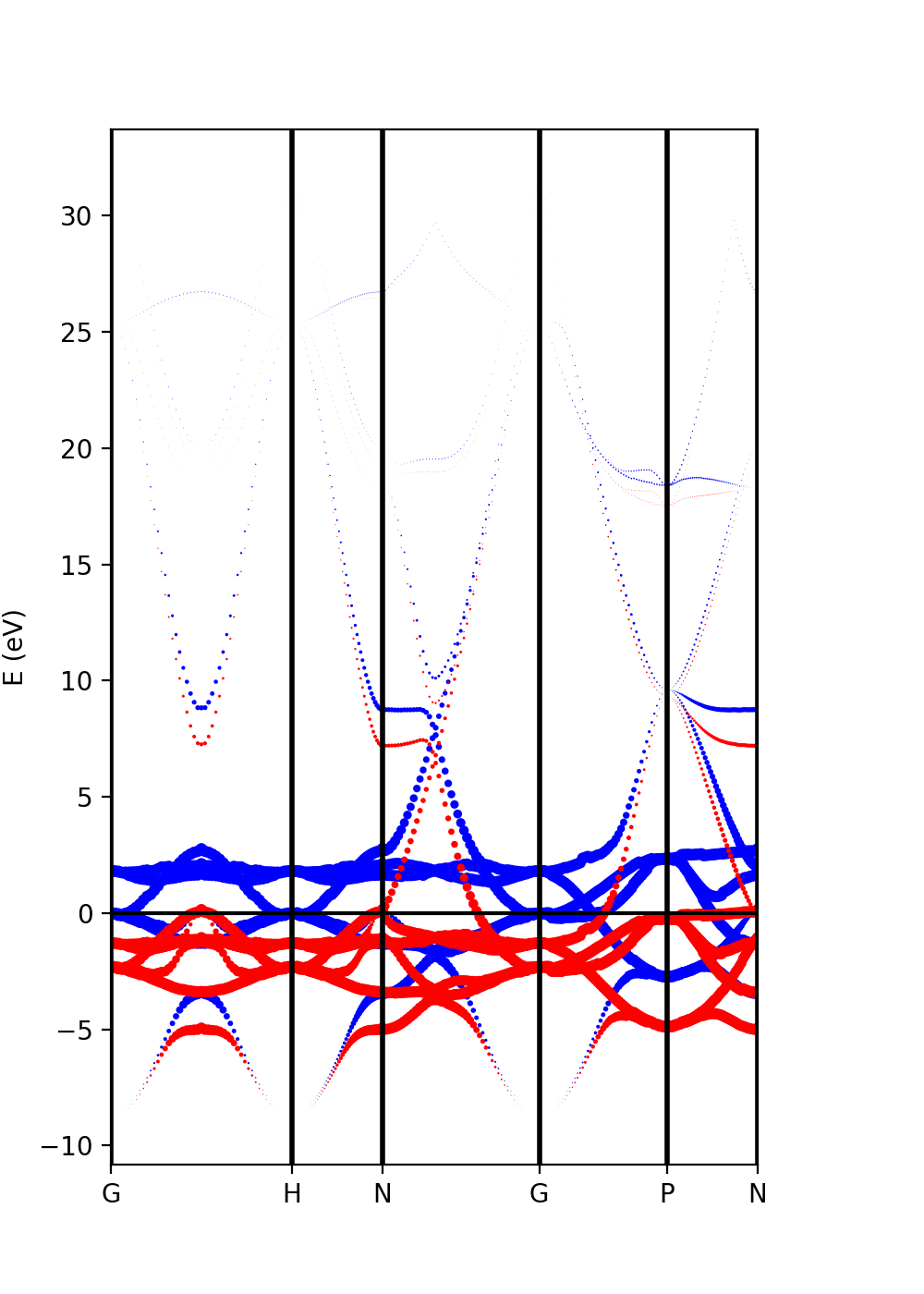
The analysis of the projected atomic orbitals is also implemented. In this case the results are more cumbersome because the projection is separated in spin up and down channels.
Let us look first at the file plot-qe-orbitals-size.
We can use the dot size as a function of the weight of the orbitals
# Automatic selection of the states s = band.get_states_helper(orbital_query=['s']) p = band.get_states_helper(orbital_query=['p']) d = band.get_states_helper(orbital_query=['d'])
and the plots are done with
band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=s,color='pink',color_2='black') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=p,color='green',color_2='orange') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=d,color='red',color_2='blue')
As an example, we can select just the d orbitals by commenting the first two plots and then running the file:
plot-qe-orbitals-size.py
From the plot is clear that d orbitals are mainly localized around the Fermi energy. The plot above is in red and blue, while the default choice in your script should be pink and black. You can experiment with the colors and other matplotlib plot options and also plot the other orbital types.
Another option is to plot the orbital composition as a colormap running the file:
plot-qe-orbitals-colormap.py
Here we have added the p and d orbitals in the analysis:
p = band.get_states_helper(orbital_query=['p']) d = band.get_states_helper(orbital_query=['d']) band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',cmap2='rainbow',selected_orbitals=p,selected_orbitals_2=d)
The colormap bar is added in the same way as in Tutorial 1 (see script), but this time we have a different colormap for each spin polarisation.
YAMBO: deal with the databases
Let us now move to the directory containing some precalculated yambo databases:
cd ../../databases_yambopy
Tutorial 3: generating the Yambo SAVE via command line
Yambopy offers a set of command line options. In order to review them, you can type
yambopy
which will print the output
yambopy v0.4
Available commands are:
plotem1s -> Plot em1s calculation
analysebse -> Using ypp, you can study the convergence of BSE calculations in 2 ways:
analysegw -> Study the convergence of GW calculations by looking at the change in band-gap value.
plotexcitons -> Plot excitons calculation
addqp -> Add corrections from QP databases.
mergeqp -> Merge QP databases
save -> Produce a SAVE folder
gkkp -> Produce a SAVE folder including elph_gkkp databases
bands -> Script to produce band structure data and visualization from QE.
serial -> Script to update serial numbers of yambo ndb.* databases in order to import them to new calculations.
gwsubspace -> Script to calculate off-diago corrections of yambo ndb.QP databases in order to plot band structure.
phinp -> Script to update the explicit list of q-points in a ph input file (ldisp=.false., qplot=.true.).
convert -> Script to convert RL number in Ry energy units using ndb.gops.
bsesize -> Script to calculate the expected BSE kernel size, in GB, to be loaded by each MPI task
l2y -> Calculate gauge-invariant electron-phonon matrix elements with LetzElPhC and convert them into Yambo format
test -> Run yambopy tests
By typing in one of the options, additional information about how to run the commands will be printed, e.g.:
yambopy save Produce a SAVE folder Arguments are: -nscf, --nscf_dir -> Path to nscf save folder -y, --yambo_dir -> <Optional> Path to yambo executables
Remember to load the yambo module, so that yambopy has access to the p2y and yambo executables.
module use /leonardo/pub/userexternal/nspallan/spack-0.22.2-06/modules module load yambo/5.3.0--intel-oneapi-mpi--2021.12.1--oneapi--2024.1.0
The quantum espresso save for hBN is provided in the directory BSE_saves/QE_saves/hBN.save (you can check the contents of the various folders).
Then, following the instructions printed on screen, we can generate a yambo SAVE from the hBN.save by typing
yambopy save -nscf BSE_saves/QE_saves/hBN.save
This should produce a SAVE folder in the current directory.
Tutorial 4: Lattice intro (plot k-point coordinates in IBZ/BZ)
For this section we will use the script bz_plot.py.
By inspecting the SAVE folder we have just generated, we will find the ns.db1 database which contains all the geometry and lattice information.
We are now going to read it in python by using the Yambopy class YamboLatticeDB, which can be instanced like this:
from yambopy import YamboLatticeDB ylat = YamboLatticeDB.from_db_file(filename="PATH/TO/SAVE/ns.db1")
(remember to edit the variable save_path in order to point at your yambo SAVE).
The ylat object now contains many useful information as attributes, such as the k-points in Cartesian or crystal coordinates, the system symmetries, lattice constants and basis vectors in real and reciprocal space, etc.
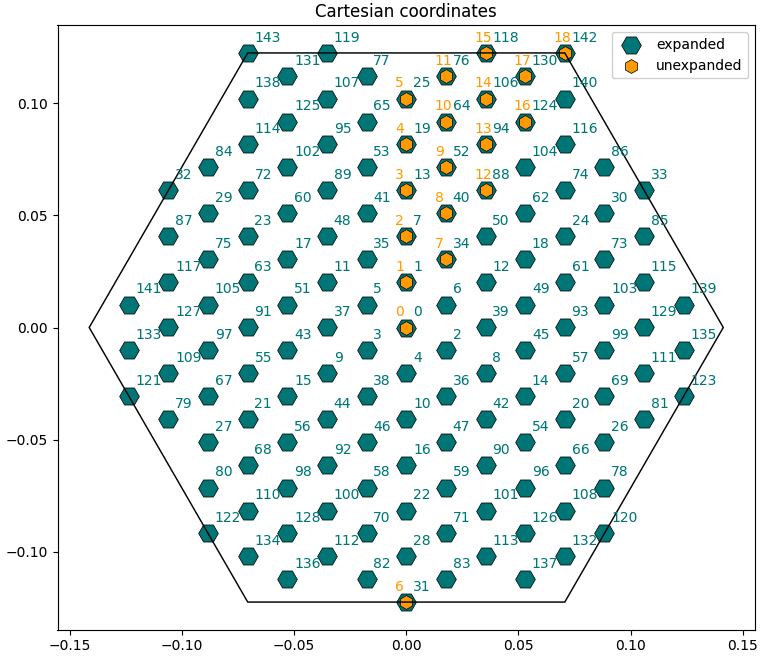
The k-points are also automatically expanded in the full Brillouin zone from the irreducible one (you can turn this off with the option Expand=False).
Directly printing the object with
print(ylat)
will also give us some general parameters related to the database.
Now check the bz_plot.py script. You will see that it performs three plots:
- Scatterplot of the k-points in Cartesian coordinates with both expanded and unexpanded grids, with annotated indices [
Cartesian_Plot=True]. - Scatterplot of the k-points in crystal coordinates [
Crystal_Plot=True]. - Manual transformation of a chosen k-point from irreducible to full Brillouin zone (you can change the index
i_kin the script to check different cases) [Symmetry_Plot=True].
Have a look at the script to understand which methods and attributed of the class YamboLatticeDB are used.
Tutorial 5: Dipoles intro (plots of dipoles on BZ, plot of IP absorption)
In this section we will use the script dipoles_plot.py and read the dipole databases generated in an optical absorption calculation by yambo. Keep in mind that from now on we will use the "BSE" yambo SAVE generated in the first section.
The databases written after a calculation of optical properties with yambo (dipoles, RPA dielectric function, excitons) are in the directory BSE_saves/BSE_databases. Here we will also find ndb.dipoles which is needed now, since it contains the matrix elements d_{vck}(\alpha) where vk and ck are the valence and electron states involved in the transition and \alpha the polarisation direction of the external electric field.
In order to read it in python we use the Yambopy class YamboDipolesDB, which can be instanced like this:
ydip = YamboDipolesDB(ylat,save='path/to/BSE/databases',filename='ndb.dipoles')
(notice that it requires a previous instance of YamboLatticeDB).
In addition, in order to read the Kohn-Sham energies, we can also instance the YamboElectronsDB as
yel = YamboElectronsDB.from_db_file(folder='path/to/SAVE')
The object ydip now has a method that permits to retrieve the independent-particle absorption spectrum with customly chosen energy range, steps, and broadening:
w, eps2 = ydip.ip_eps2(yel)
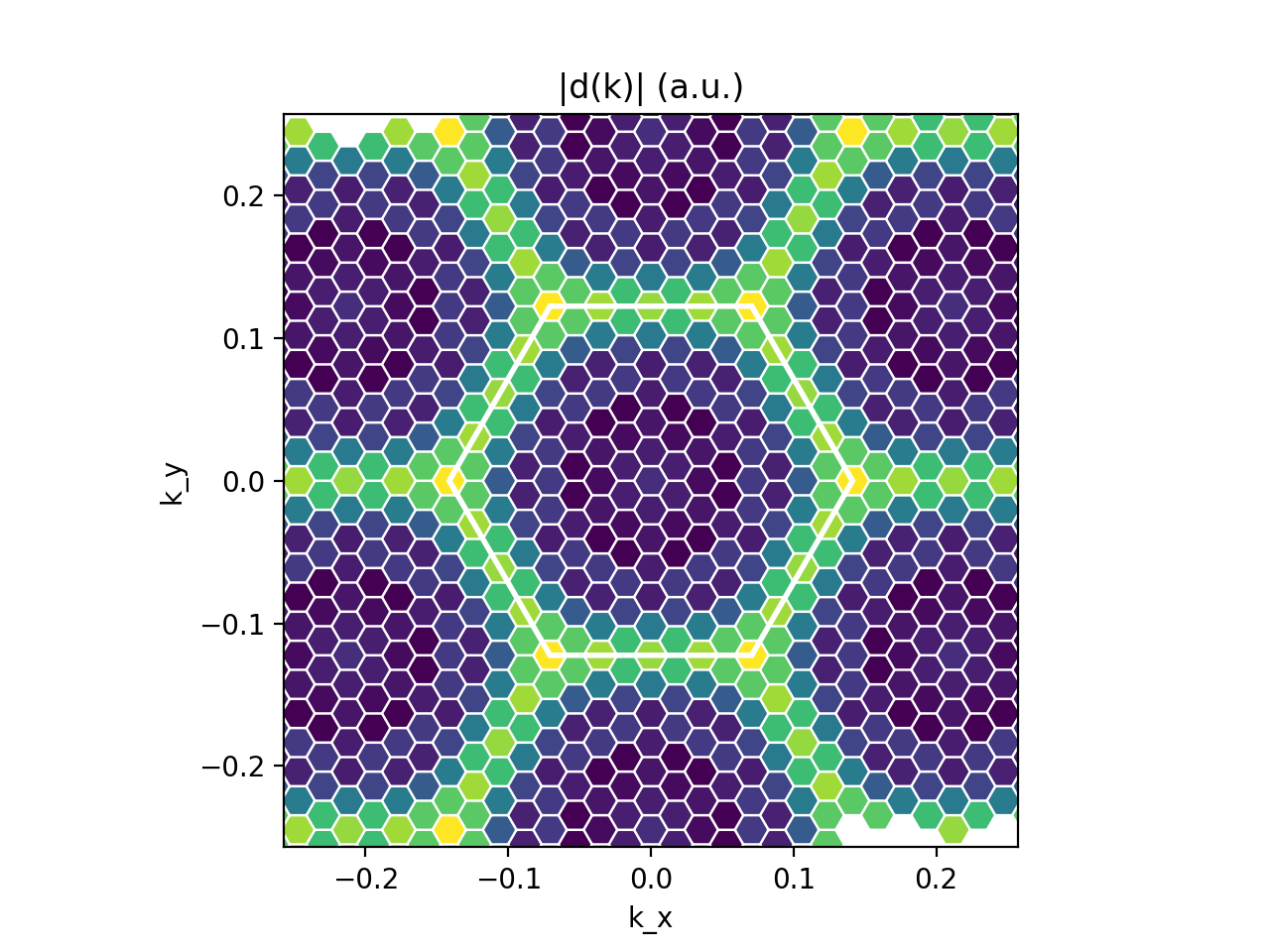
In order to see all this in action, take a look at the dipoles_plot.py script. You will see that it performs two plots:
- Plot of |d(k)| in the BZ for selected v,c and \alpha (we choose the layer plane 'xy') [
Kspace_Plot=True]. From this plot you can appreciate which sections of the BZ contribute the most to the absorption rate. - Plot of the independent-particles absorption spectrum [
Absorption_Plot=True].
You can play with the indices and the plot parameters to check what happens.
Tutorial 6: Dielectric function
The dielectric function in the RPA approximation is a crucial quantity that yambo needs to compute both for GW calculations (including its frequency dependence via plasmon-pole approximation or more advanced methods) and BSE spectra (here only the static part is needed).
However, this function is stored in a binary database that needs to be accessed in order to plot it. In this example, we have the static dielectric function stored in BSE_saves/BSE_databases, in a series of databases called ndb.em1s (one fragment per q point).
We can read these databases with the class YamboStaticScreeningDB as it is done in the script em1s.py. The docstring of the script provides useful information into the form in which the dielectric function is actually stored and how to convert into either the inverse microscopic dielectric function (a tensor in G-space) or the macroscopic dielectric function itself.
yem1s = YamboStaticScreeningDB(save=save_path+'/SAVE',em1s=bse_path)
Printing information on this object returns the main information needed to understand the origin of the database: number of bands included, number of reciprocal lattice vectors, type of 2D cutoff used (if any), etc.
print(yem1s)
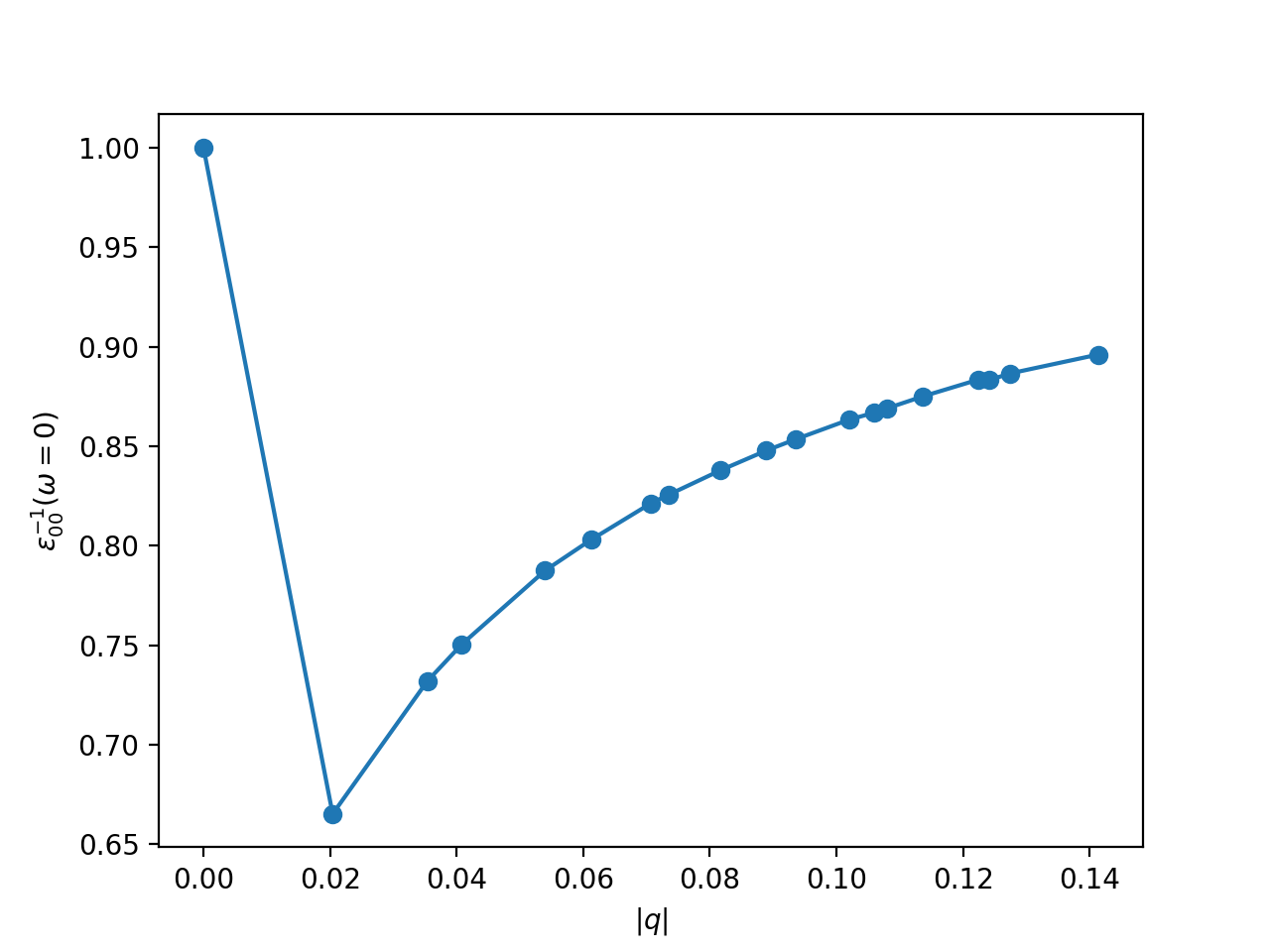
You can then produce a plot of these quantities for 2D hBN (below the head of the inverse dielectric function):
yem1s.plot_epsm1(ax1,ng1=0,ng2=0,ls='-',marker='o')
As you can see, at small momenta the inverse dielectric function sharply rises to 1 in a 2D system. This is why a very dense reciprocal-space sampling (or advanced techniques such as the RIM-W) is required to converge it.
Links
- Proceed to Modena 2025 : Yambopy part 2
- Back to Modena 2025