A fast approach to excitonic effects in linear/non-linear response
In this tutorial we show a fast but approximated approach to include electron-hole interaction in the linear and non-linear response,
using a real-time approach.
These features will available in Yambo 5.4
Introduction
In this tutorial we suppose that you are already familiar with linear/non-linear response in real-time
and also correlation effects in this kind of simulations. If it is not the case please have a look to the tutorials:
- Linear response using Dynamical Berry Phase
- Real time approach to non-linear response (SHG)
- Correlation effects in the non-linear response
In this tutorial we will use an approximation for the screened exchange that consist in taking into account only
the long-range part of the screened interaction [math]\displaystyle{ W(q+G, q+G') }[/math], namely [math]\displaystyle{ q\neq= }[/math] and [math]\displaystyle{ G, G'=0 }[/math],
and do not consider local field effects generated by the Hartree term.
We will see at the end of this tutorial how this approximation can be systematically improved.
Setup calculations
In this tutorial we will take as example the two dimensional hBN.
DFT wave-functions and inputs can be downloaded here: hBN-2D-RT.tar.gz.
First of all run the setup, then remove symmetries along the y direction, as explained in the tutorial above.
Calculate the dielectric constant
Calculate the dielectric constant that will be used to construct the screened exchange, with the command: yambo -X s
screen # [R] Inverse Dielectric/Response Matrix em1s # [R][Xs] Statically Screened Interaction dipoles # [R] Oscillator strenghts (or dipoles) DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc % BndsRnXs 1 | 20 | # [Xs] Polarization function bands % NGsBlkXs= 3000 mHa # [Xs] Response block size % LongDrXs 0.000000 | 1.000000 | 0.000000 | # [Xs] [cc] Electric Field %
Once the calculation of [math]\displaystyle{ \epsilon(\omega=0; q+G, q+G') }[/math] is finished we can run the real-time simulation using the LSEX correlation.
Nota bene: Screening has to be calculated with yambo executable and not yambo_nl
Real-time setup and calculations
In order to generate input file for a single real-time calculation for linear response we use the command: yambo_nl -u p -V qp
In this input we select LSEX as correlation type.
nloptics # [R] Non-linear spectroscopy DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles NL_Threads=0 # [OPENMP/NL] Number of threads for nl-optics % NLBands 3 | 6 | # [NL] Bands range % NLverbosity= "high" # [NL] Verbosity level (low | high) NLtime= 55.000000 fs # [NL] Simulation Time NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= " LSEX" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX") NLLrcAlpha= 0.000000 # [NL] Long Range Correction NLDamping= 0.100000 eV # [NL] Damping (or dephasing) RADLifeTime=-1.000000 fs # [RT] Radiative life-time (if negative Yambo sets it equal to Phase_LifeTime in NL) #EvalCurrent # [NL] Evaluate the current #FrPolPerdic # [DIP] Force periodicity of polarization respect to the external field HARRLvcs= 1 RL # [HA] Hartree RL components EXXRLvcs= 1 RL # [XX] Exchange RL components CORRLvcs= 1 RL # [XX] Correlation RL components GfnQPdb= "none" # [EXTQP G] Database action GfnQP_INTERP_NN= 1 # [EXTQP G] Interpolation neighbours (NN mode) GfnQP_INTERP_shells= 20.00000 # [EXTQP G] Interpolation shells (BOLTZ mode) GfnQP_DbGd_INTERP_mode= "NN" # [EXTQP G] Interpolation DbGd mode % GfnQP_E 3.000000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim % GfnQP_Z= ( 1.000000 , 0.000000 ) # [EXTQP G] Z factor (c/v) GfnQP_Wv_E= 0.000000 eV # [EXTQP G] W Energy reference (valence) % GfnQP_Wv 0.000000 | 0.000000 | 0.000000 | # [EXTQP G] W parameters (valence) eV| 1|eV^-1 % GfnQP_Wv_dos= 0.000000 eV # [EXTQP G] W dos pre-factor (valence) GfnQP_Wc_E= 0.000000 eV # [EXTQP G] W Energy reference (conduction) % GfnQP_Wc 0.000000 | 0.000000 | 0.000000 | # [EXTQP G] W parameters (conduction) eV| 1 |eV^-1 % GfnQP_Wc_dos= 0.000000 eV # [EXTQP G] W dos pre-factor (conduction) % Field1_Freq 0.100000 | 0.100000 | eV # [RT Field1] Frequency % Field1_NFreqs= 1 # [RT Field1] Frequency Field1_Int= 1000.00 kWLm2 # [RT Field1] Intensity Field1_Width= 0.000000 fs # [RT Field1] Width Field1_kind= "DELTA" # [RT Field1] Kind(SIN|SOFTSIN| see more on src/modules/mod_fields.F) Field1_pol= "linear" # [RT Field1] Pol(linear|circular) % Field1_Dir 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor %
This option LSEX correspond to the use of the long-range part only of the screened interaction [math]\displaystyle{ W(q) }[/math] and disregard the terms with [math]\displaystyle{ G\neq 0 }[/math].
This approximation is valid for system that are homogenous in the direction of the response we are interested in.
For example in the system studied here, monolayer hBN, you will see that this approximation give results similar to the full calculation.
This can be not the case for inhomogeneous systems.
After the run time simulation results can be analysed with ypp_nl:
nonlinear # [R] Non-linear response analysis Xorder= 1 # Max order of the response/exc functions % TimeRange -1.000000| -1.00000 | fs # Time-window where processing is done % ETStpsRt= 400 # Total Energy steps % EnRngeRt 0.00000 | 20.00000 | eV # Energy range % DampMode= "NONE" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) DampFactor= 0.000000 eV # Damping parameter PumpPATH= "none" # Path of the simulation with the Pump only
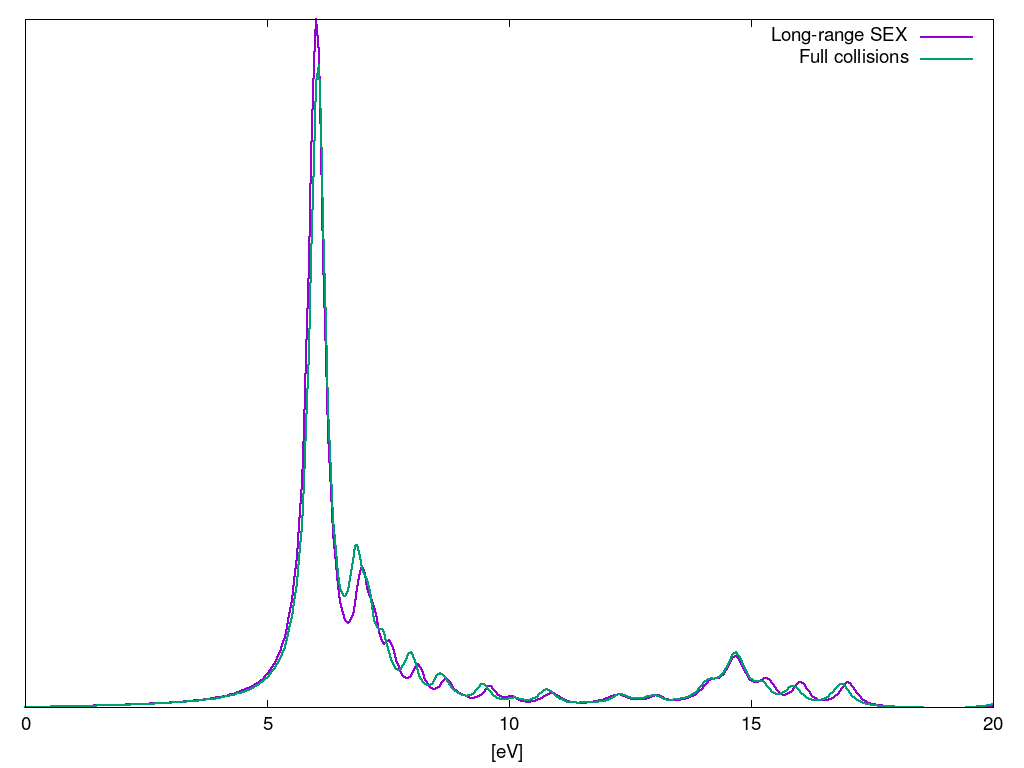
In the figure below we compare result obtained with the full collisions [ Real time Bethe-Salpeter Equation (TDSE) ] with the one using only Long-range part of the screened-exchaned without local field effects (HARRLvcs = 1).
As you can see in the case of monolayer hBN results are very close, and the long-rang screened exchange only is a good approximation.
Improving long-range SEX approximation
Using the present approach you can also decide to go beyond the long-range only part of SEX and include G-vector dependence of W in SEX plus local field effects.
In order to do so you can repeat calculation increasig number of G-vectors in exchange, screening and Hartree by changing these variables:
HARRLvcs= 1,3,5,etc.. RL # [HA] Hartree RL components EXXRLvcs= 1,3,5,etc.. RL # [XX] Exchange RL components CORRLvcs= 1,3,5,etc.. RL # [XX] Correlation RL components
and repeat the calculation for larger number of G-vectors: 1,3,5,..etc.. notice that calculations become immediately very expensive
but for many system few G-vectors are enought
to converge to the full collisions result.