Bethe-Salpeter solver: SLEPC
In this module you learn how to obtain the optical absorption spectrum of bulk BN within the Bethe-Salpeter equation (BSE) framework for a previously calculated Bethe-Salpeter kernel. You will learn how to by-pass the diagonalization of the full two-particle Hamiltonian and only obtain eigenvalues and eigenvectors for a selected number of states, using the SLEPc solver.[1]
Prerequisites
- You must first complete the Static screening and Bethe-Salpeter kernel modules in the step-by-step guide
- Optionally, in order to compare results with the diagonalization solver, you may first complete the Bethe-Salpeter solver: diagonalization module.
- Optionally, in order to better understand background, you may first complete the Bethe-Salpeter solver: Lanczos-Haydock module and the How to analyse excitons module.
You will need:
- The
SAVEdatabases for 3D hBN - The
3D_BSEdirectory containing the databases from the Static screening and Bethe-Salpeter kernel modules - The
yamboexecutable gnuplotfor plotting spectra
Choice of input parameters
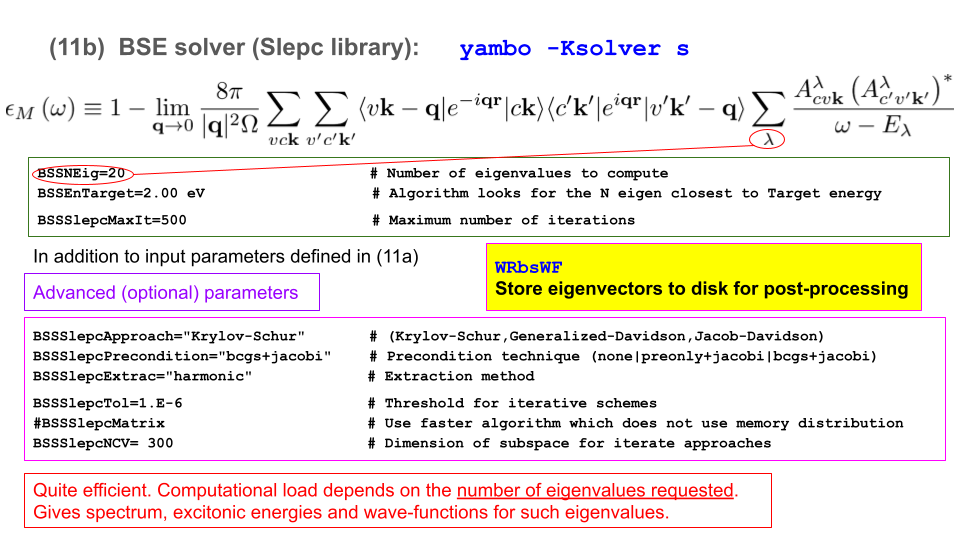
To use the SLEPc solver invoke yambo with "-y s" option in the command line:
$ yambo -F 03_3D_BSE_slepc_solver.in -y s -V qp -J 3D_BSE
The input is open in the editor. The input variables to be changed are
% BEnRange 2.00000 | 8.00000 | eV % BEnSteps= 200 % BDmRange 0.10000 | 0.10000 | eV % % BLongDir 1.000000 | 1.000000 | 0.000000 | % % KfnQP_E 1.440000 | 1.000000 | 1.000000 | %
as for the diagonalization and Haydock solvers, while the additional parameters
BSSNEig= 4 BSSEnTarget= 2.00 eV
define the number of states to look for and the energy around which to look, respectively.
In our case, we know that the optical absorption onset is >4 eV, so by setting BSSEnTarget=2.00 eV we will capture the lowest-energy BSSNEig states of the absorption spectrum.
We set BSSNEig=4 since we know from the tutorial on how to analyse excitons that the first peak in the hBN spectrum is comprised of states 3 and 4:
$ ls o-3D_BSE.exc_qpt1_E_sorted
# E [ev] Strength Index
#
3.53959870 0.575763806E-6 1.00000000
3.53977442 0.104714145E-4 2.00000000
3.58167791 0.482294828 3.00000000
3.58199883 1.00000000 4.00000000
3.70031905 0.913734333E-8 5.00000000
3.71410418 0.229000130E-8 6.00000000
... ... ...
4.24574852 0.303127885 12.0000000
4.24597263 0.125847101 13.0000000
... ... ...
4.49848938 0.813002646 20.0000000
4.49882555 0.353004009 21.0000000
Therefore we are trying to describe just the dominant feature in the spectrum.
There is also an additional parameter defining the maximum number of iterations:
BSSSlepcMaxIt=0
If we keep this equal to zero, the code will use an internally defined value.
Bethe-Salpeter solver runlevel
Invoke yambo to run the calculation:
$ yambo -F 03_3D_BSE_slepc_solver.in -J "3D_BSE-NEig4,3D_BSE"
This outputs the following log:
...
<---> [03] BSE solver(s) @q1
<---> [03.01] Slepc Solver @q1
<---> [SLEPC] Slower alogorithm but BSE matrix distributed over MPI tasks
<---> [SLEPC] Approach : Krylov-Schur
<---> [SLEPC] Extraction method : ritz
<---> [SLEPC] Number of requested eigenvalues : 4
<---> [SLEPC] Criterion is target energy : 2.000000 [eV]
<---> [SLEPC] Stopping condition tolerance : 0.100000E-5
<---> [SLEPC] Stopping condition max iterations : -2
<---> [SLEPC] Iteration #1 - converged States 0 - error : 0.013375 0.000000
...
<---> [SLEPC] Iteration #8 - converged States 0 - error : 0.229377E-5 0.00000
<---> [SLEPC] Iteration #9 - converged States 3 - error : 0.726125E-7 0.121157E-5
<---> [SLEPC] Iteration #10 - converged States 5 - error : 0.247454E-7 0.712303E-5
<---> [SLEPC] Number of iterations : 10
<---> [SLEPC] Number of eigenvalues [NEV]: 4
<---> [SLEPC] Max. subspace size of solver [NCV]: 19
<---> [SLEPC] Max. allowed dim [MPD]: 19
<---> [SLEPC] Number of converged states : 5
...
As you can see, the requested eigenvalues were converged. You may notice some advanced information (Approach, Extraction method, Stopping condition tolerance, etc). These are all controllable with specific input variables (see the yambo cheatsheet for more information), but in practice you don't usually need to worry about them.
If you now check inside the folder 3D_BSE-NEig4, you will see that a database ndb.BS_diago_Q1 has been produced, like in the full diagonalization case. This will allow postprocessing and analysis of the requested excitons with ypp.
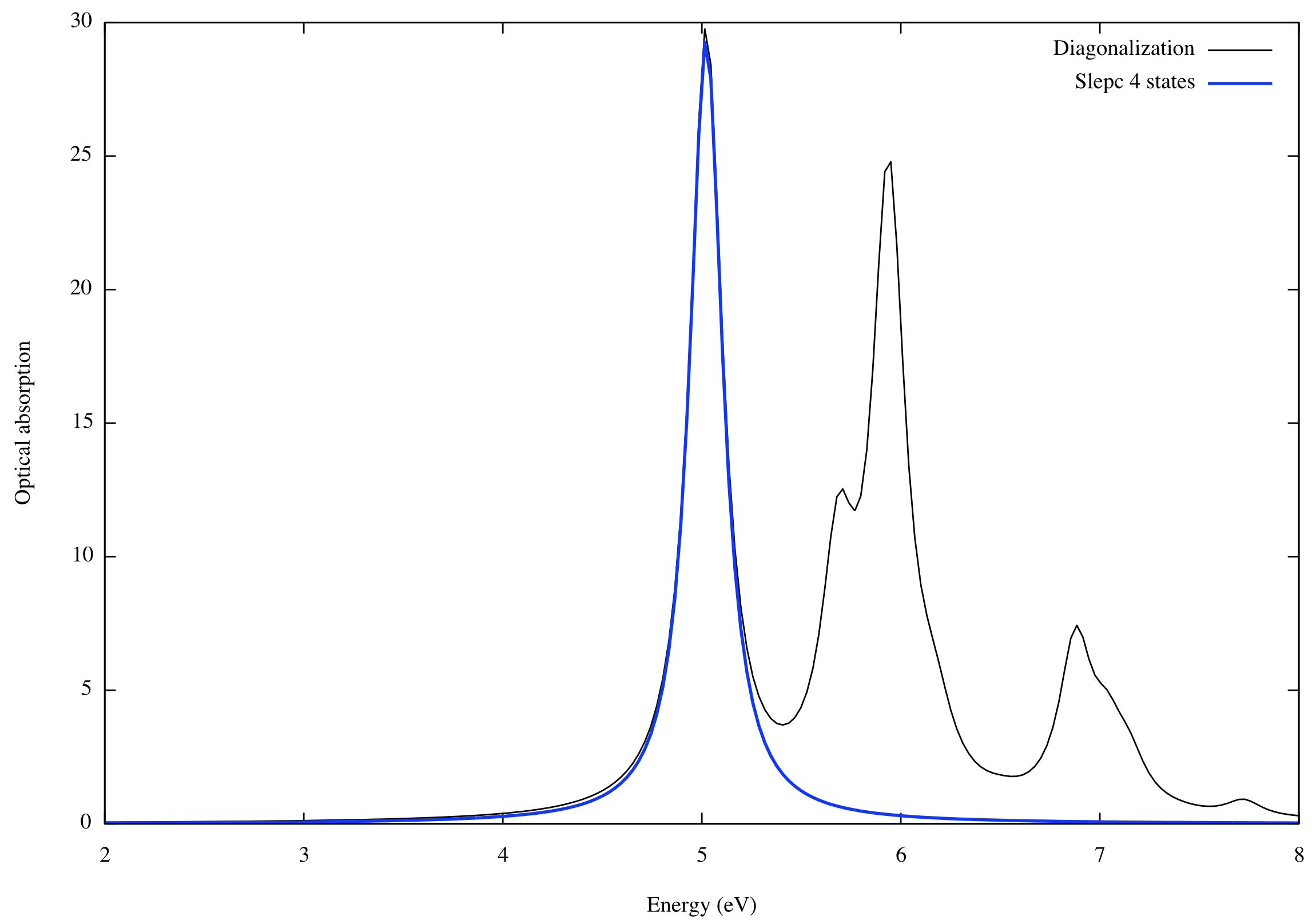
We can plot the spectrum from the o-* file and compare with the result from diagonalization:
$gnuplot ... plot 'o-3D_BSE.eps_q1_diago_bse' u 1:2 w l lc rgb 'black' t 'Diagonalization', 'o-3D_BSE-NEig4.eps_q1_slepc_bse' u 1:2 w l lw 2 lc rgb 'blue' t 'Slepc 4 states'
As expected, by requesting the first 4 states we are able to reproduce the first and strongest absorption peak.
Including more peaks
We now want to also include the second and third bright peaks in the calculations. From the *E_sorted file, we know that the second bright peak corresponds to states 12 and 13.
Change therefore the input variable:
BSSNEig= 13
and repeat the calculation
$ yambo -F 03_3D_BSE_slepc_solver.in -J "3D_BSE-NEig13,3D_BSE"
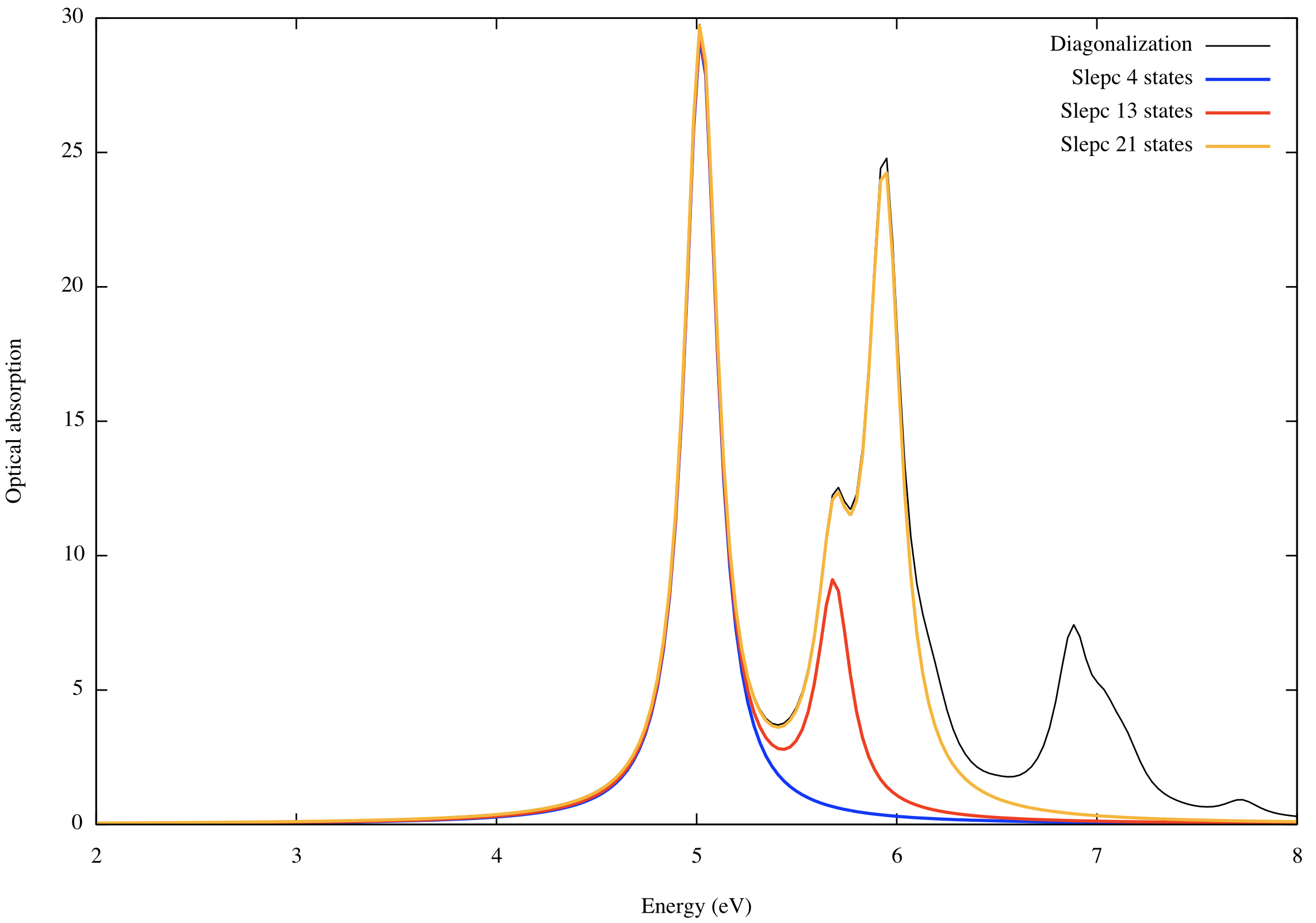
As you can see from the plot below, we now capture the second peak as well, though it lacks the enhancement due to the low-energy shoulder of the adjacent third peak. In order to include the third peak change again the input variable:
BSSNEig= 21
and again repeat the calculation
$ yambo -F 03_3D_BSE_slepc_solver.in -J "3D_BSE-NEig21,3D_BSE"
By plotting these results:
$ gnuplot ... plot 'o-3D_BSE.eps_q1_diago_bse' u 1:2 w l lc rgb 'black' t 'Diagonalization', 'o-3D_BSE-NEig4.eps_q1_slepc_bse' u 1:2 w l lw 2 lc rgb 'blue' t 'Slepc 4 states', 'o-3D_BSE-NEig13.eps_q1_slepc_bse' u 1:2 w l lw 2 lc rgb 'red' t 'Slepc 13 states', 'o-3D_BSE-NEig21.eps_q1_slepc_bse' u 1:2 w l lw 2 lc rgb 'orange' t 'Slepc 21 states'
We see that we obtain an accurate description of the relevant part of the absorption spectrum of bulk hBN by just including 21 states. The diagonalization solver needs 432 states instead, because this is the size of the two-particle Hamiltonian in our calculation (keep in mind that this is far from being numerically converged, and the correct absorption spectrum looks quite different).
In a real calculation for a large system, when full diagonalization is not an option, you will typically first obtain the full absorption spectrum using the Lanczos-Haydock solver, then switch to the SLEPc to focus on the exciton states relevant to your analysis, while using the previously obtained full spectrum as a reference as we did in this tutorial.
Summary
From this tutorial you've learned:
- How to compute the optical spectrum by using the SLEPc solver within the Bethe-Salpeter equation framework
- How to correctly describe a subset of the excitonic eigenvalues and eigenvectors without diagonalizing the full two-particle Hamiltonian.
Links
- Previous module: Bethe-Salpeter kernel
- Alternative Bethe-Salpeter equation solver: diagonalization
- Alternative Bethe-Salpeter equation solver: Haydock
- Back to Rome 2023#Tutorials
- Back to Calculating optical spectra including excitonic effects: a step-by-step guide tutorial
- Back to tutorials menu
- Back to technical modules menu
References
- ↑ V. Hernandez, J.E. Roman and V. Vidal in ACM Transactions on Mathematical Software, 31 315 (2005)