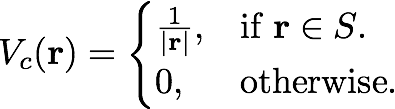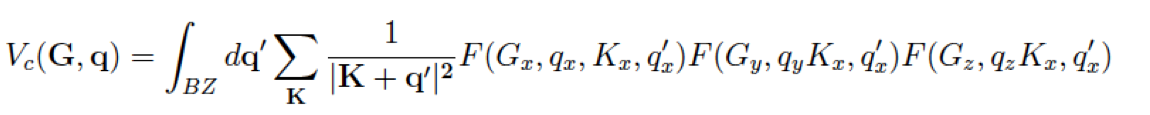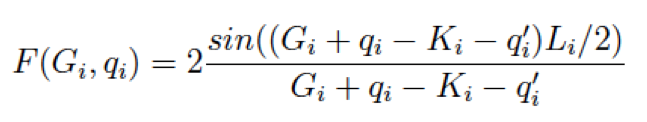How to treat low dimensional systems
In this tutorial you will learn how to:
- Avoid numerical divergences using the Random Integration Method (RIM)
- Generate a truncated coulomb potential with a box-like cutoff to eliminate the image-image interactions
- Use the truncated coulomb potential in the GW calculation
- Use the truncated coulomb potential in the BSE calculation
- Analyze the difference with corresponding calculations without the use of a truncated potetnial
Prerequisites
SAVEfolder for 2D hBN generated with a 6x6x1 k-gridyamboexecutableyppexecutablegnuplot, for plotting spectra- Complete the Generating the Yambo databases tutorial
- Run Initialization
Avoid numerical divergences using the Random Integration Method (RIM)
In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) This can create numerical problems in the convergence of the many-body results due to the divergence at small q of the coulomb potential (which appears in all the main equations, see i.e. the exchange self-energy equation).
To eliminate this problem YAMBO uses the so-called Random Integration Method which means to use a Monte Carlo Integration with Random Q-points whose number RandQpts is given in input.
Create the input to generate the ndb.RIM database
$ yambo -F yambo_RIM.in -r
and change the following variable
RandQpts= 1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components
N.B RandGvec=100 means to use the RIM for the first 100 G-components of the coulomb potential
(Suggestion : later you can check convergence of the HF gap changing these two values)
Close input and Run yambo
$ yambo -F yambo_RIM.in -J 2D
At the end in the 2D directory you find a new database and a new report file r-2D_rim_cut is also present. Open it and look inside
[04.02] RIM integrals
=====================
Gamma point sphere radius [au]: 0.08028
Points outside the sphere : 800231
[Int_sBZ(q=0) 1/q^2]*(Vol_sBZ)^(-1/3) = 7.667102
should be < 7.795600
[WR./2D//ndb.RIM]-------------------------------------------
Brillouin Zone Q/K grids (IBZ/BZ): 7 36 7 36
Coulombian RL components : 209
Coulombian diagonal components :yes
RIM random points : 1000000
RIM RL volume [a.u.]: 0.390129
Real RL volume [a.u.]: 0.390112
Eps^-1 reference component :0
Eps^-1 components : 0.00 0.00 0.00
RIM anysotropy factor : 0.000000
- S/N 005962 -------------------------- v.04.01.02 r.00120 -
Summary of Coulomb integrals for non-metallic bands |Q|[au] RIM/Bare:
Q [1]:0.1000E-40.9835 * Q [2]: 0.256404 1.093779 Q [5]: 0.444104 1.031700 * Q [3]: 0.512807 1.023425 Q [6]: 0.678380 1.013439 * Q [4]: 0.769211 1.010447 Q [7]: 0.888208 1.007869
Close the report file and perform a calculation of the exchange self-energy to estimate the HF gap using the RIM.
Generate the input
$ yambo -F yambo_HF.in -r -x -J 2D
In order to calculate the HF gap only for the last k-point, change the last line as
QPkrange # [GW] QP generalized Kpoint/Band indices 7| 7| 4| 5|
Close the input and run yambo
$ yambo -F yambo_HF.in -J 2D
At the end you will find the report file r-2D_HF_and_locXC_rim_cut
and the output file o-2D.hf . Open it and have a look
K-point Band Eo Ehf DFT HF
7.00000 4.00000 0.00000 -3.21640 -16.21949 -19.43589 7.00000 5.00000 4.40109 9.68783 -11.10752 -5.82078
The HF gap is 12.91 eV obtained subtracting the 2 values in the fourth column
Doing a similar HF calculation without generating and reading the RIM database the HF gap results to be 12.69 eV. Indeed the presence of the numerical instability is evident only using denser k-grids with respect to the one used in this Tutorial (6x6x1). Suggestion: later you can generate other SAVE directories with denser k-grids and check the HF gap. The results of the HF gap calculated with different k-grids without (noRIM) and with Random Inetgration Method (RIM) to show up the problem are reported:
noRIM RIM
6x6x1 12.69eV 12.91eV 12x12x1 12.80eV 12.89eV 15x15x1 12.96eV 12.90eV 45x45x1 15.52eV 12.96eV
So the home message is : use always the RIM in MB simulations of low-dimensional materials.
Generate a truncated coulomb potential/ndb.cutoff database (yambo -r)
To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. ) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.
In YAMBO you can use :
spherical cutoff (for 0D systems) cylindrical cutoff (for 1D systems) box-like cutoff (for 0D, 1D and 2D systems)
The Coulomb potential with a box-like cutoff is defined as
Then the FT component is
where
For a 2D-system with non period direction along z-axis we have
Important remarks:
- the Random Integration Method (RIM) is required to perform the Q-space integration
- for sufficiently large supercells a choose L_i slightly smaller than the cell size in the i-direction ensures to avoid interaction between replicas
Create the input file:
$ yambo -F yambo_cut2D.in -r -J 2D (N.B. adding option -J 2D allows to read the variables of the previous run)
Change the following variables as:
CUTGeo= "box z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. % CUTBox 0.00 | 0.00 | 32.0 | # [CUT] [au] Box sides
Close the input file and run yambo:
$ yambo -F yambo_cut2D.in -J 2D
in the directory 2D you will find a new database ndb.cutoff