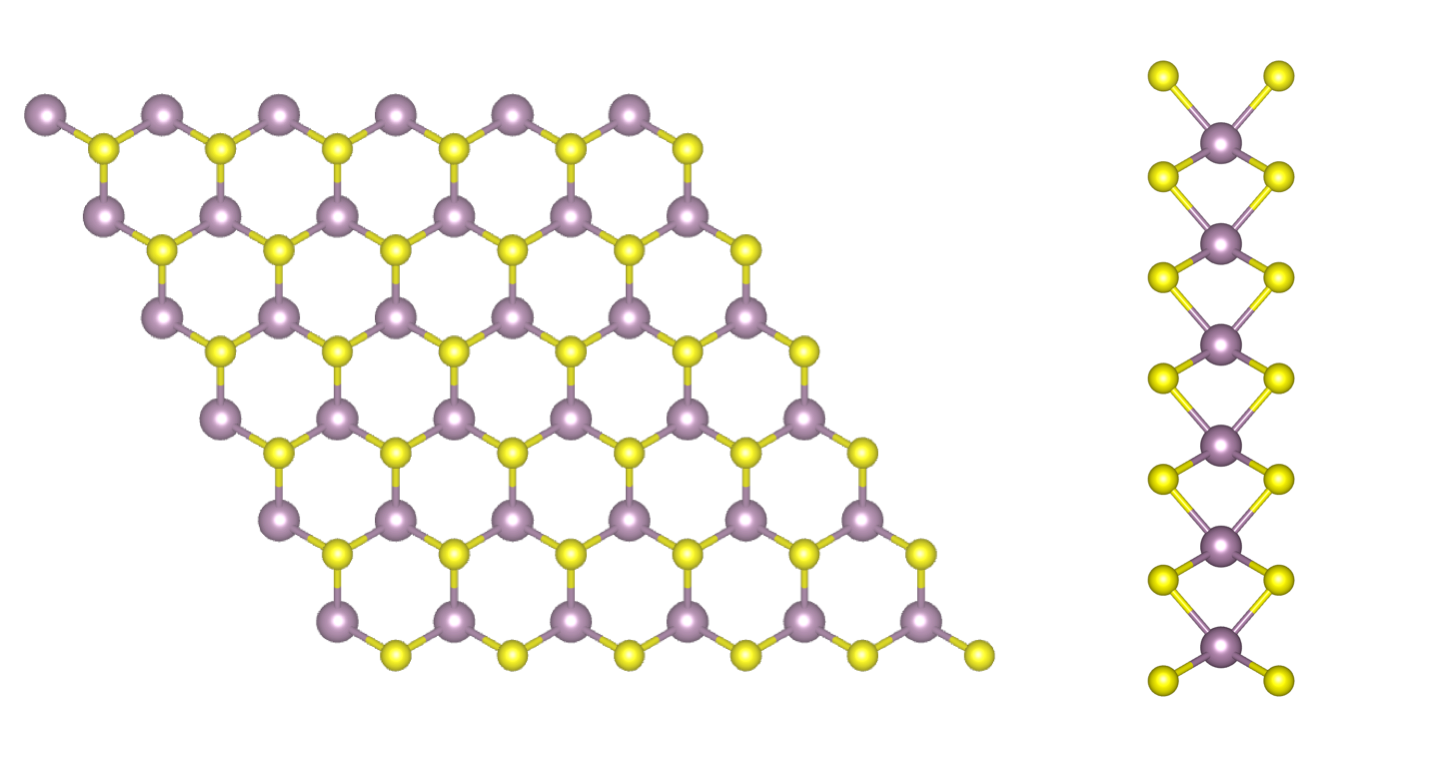
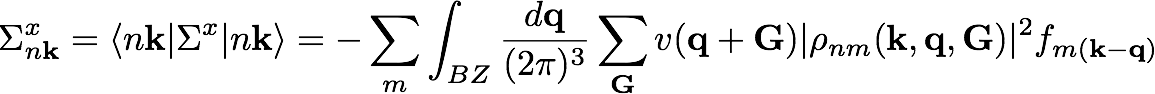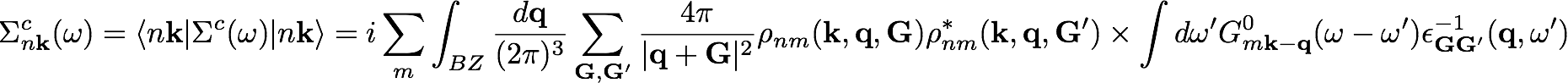Quasi-particles of a 2D system
In this tutorial you will compute the quasiparticle corrections to the band structure of a free-standing single layer of MoS2. Aim of the tutorial is to learn how to efficiently run a GW simulation in a 2D material based on:
- Acceleration techniques of GW, some of which specific for 2D systems
- Parallelization techniques
In the end, you will obtain a quasiparticle band structure based on the simulations, the first step towards the reproduction of an ARPES spectrum. Beware: we won’t use fully converged parameters, so the final result should not be considered accurate.
Step 1: Speeding up the self-energy convergence in the k-grid
In this section, you will learn to use two algorithms present in Yambo that lead to a speed up of the self-energy convergence with respect to the k-grid.
To appreciate the impact of these algorithms, let us first perform a GW computation for the monolayer of MoS2.
Enter the 01_GW_first_run folder and generate the input file:
yambo -F gw_ppa.in -p p
Modify the input file as follows:
gw0 # [R] GW approximation
ppa # [R][Xp] Plasmon Pole Approximation for the Screened Interaction
dyson # [R] Dyson Equation solver
HF_and_locXC # [R] Hartree-Fock
em1d # [R][X] Dynamically Screened Interaction
X_Threads=0 # [OPENMP/X] Number of threads for response functions
DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy
EXXRLvcs= 37965 RL # [XX] Exchange RL components
VXCRLvcs= 37965 RL # [XC] XCpotential RL components
Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% BndsRnXp
1 | 80 | # [Xp] Polarization function bands
%
NGsBlkXp= 10 Ry # [Xp] Response block size
% LongDrXp
1.000000 | 1.000000 | 1.000000 | # [Xp] [cc] Electric Field
%
PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy
XTermKind= "none" # [X] X terminator ("none","BG" Bruneval-Gonze)
% GbndRnge
1 | 80 | # [GW] G[W] bands range
%
GTermKind= "BG" # [GW] GW terminator ("none","BG" Bruneval-Gonze,"BRS" Berger-Reining-Sottile)
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g")
%QPkrange # [GW] QP generalized Kpoint/Band indices
7|7|13|14|
%
Here, consider the number of G vectors and the number of bands as already being converged. So, compute the gap at GW level:
yambo -F gw_ppa.in -J 80b_10Ry
Once terminated the computation, you can now inspect the output file o-80b_10Ry.qp.
You should have obtained a GW gap of 2.483 eV.
RIM
To understand how we can improve the calculation in the k-grid to achieve a speed-up, consider briefly again the expression of the exchange part of the self-energy
You can notice that the integration around q=0 here is problematic for the presence of a 1/q from the Coulomb potential that diverges, while all the other terms are slowly varying in q. Usually in Yambo this integration is performed analytically in a small sphere around q=0.
However, in this way the code lost part of the integral out of the circle. This usually
is not problematic because for a large number of q and k point the missing term goes to zero.
However in system that requires few k-points or even only the gamma one, it is possible
to perform a better integration of this term by adding the flag -r. So as
yambo -F gw_ppa.in -p p -r
In this manner, you generate the input:
HF_and_locXC # [R XX] Hartree-Fock Self-energy and Vxc ppa # [R Xp] Plasmon Pole Approximation gw0 # [R GW] G0W0 Quasiparticle energy levels em1d # [R Xd] Dynamical Inverse Dielectric Matrix rim_cut # [R] Coulomb potential RandQpts= 1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components CUTGeo= "slab z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere/ws/slab X/Y/Z/XY.. ...
In this input, RandGvec is the number of component of the Coulomb potential we want integrate numerically and RandQpts is the number of random points used to perform the integral by Monte Carlo.
The [CUT] keyword refers to the truncation of the Coulomb interaction to avoid spurious interaction between periodically repeated copies of the simulation supercell along the z-direction (that in this case is the non periodic direction). Keep in mind that the vacuum space between two copies of the system should be converged: here we are using 20 bohr but a value of 40 bohr would be more realistic.
If you turn on this integration you will get a slightly different band gap, but in the limit of large k points the final results will be the same of the standard method. However this correction is important for systems that converge with few k-points or with gamma only and it is applied both at the exchange and correlation part of the self-energy.
Now make a GW computation using the RIM method
gw0 # [R] GW approximation
ppa # [R][Xp] Plasmon Pole Approximation for the Screened Interaction
dyson # [R] Dyson Equation solver
HF_and_locXC # [R] Hartree-Fock
em1d # [R][X] Dynamically Screened Interaction
X_Threads=0 # [OPENMP/X] Number of threads for response functions
DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy
rim_cut # [R] Coulomb potential
RandQpts=1000000 # [RIM] Number of random q-points in the BZ
RandGvec= 100 RL # [RIM] Coulomb interaction RS components
CUTGeo= "slab z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere/ws/slab X/Y/Z/XY..
% CUTBox
0.000000 | 0.000000 | 0.000000 | # [CUT] [au] Box sides
%
CUTRadius= 0.000000 # [CUT] [au] Sphere/Cylinder radius
CUTCylLen= 0.000000 # [CUT] [au] Cylinder length
CUTwsGvec= 0.700000 # [CUT] WS cutoff: number of G to be modified
EXXRLvcs= 37965 RL # [XX] Exchange RL components
VXCRLvcs= 37965 RL # [XC] XCpotential RL components
Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% BndsRnXp
1 | 80 | # [Xp] Polarization function bands
%
NGsBlkXp= 10 Ry # [Xp] Response block size
% LongDrXp
1.000000 | 1.000000 | 1.000000 | # [Xp] [cc] Electric Field
%
PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy
XTermKind= "none" # [X] X terminator ("none","BG" Bruneval-Gonze)
% GbndRnge
1 | 80 | # [GW] G[W] bands range
%
GTermKind= "BG" # [GW] GW terminator ("none","BG" Bruneval-Gonze,"BRS" Berger-Reining-Sottile)
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g")
%QPkrange # [GW] QP generalized Kpoint/Band indices
7|7|13|14|
%
yambo -F gw_ppa.in -J 80b_10Ry_rim
You can now inspect the output file o-80b_10Ry_rim.qp. The GW gap should have increased to 4.109 eV.
RIM-W
In 2D systems, the improvement granted by the better integration around q=0 of the Coulomb potential via the RIM approach does not work well for the correlation part of self-energy
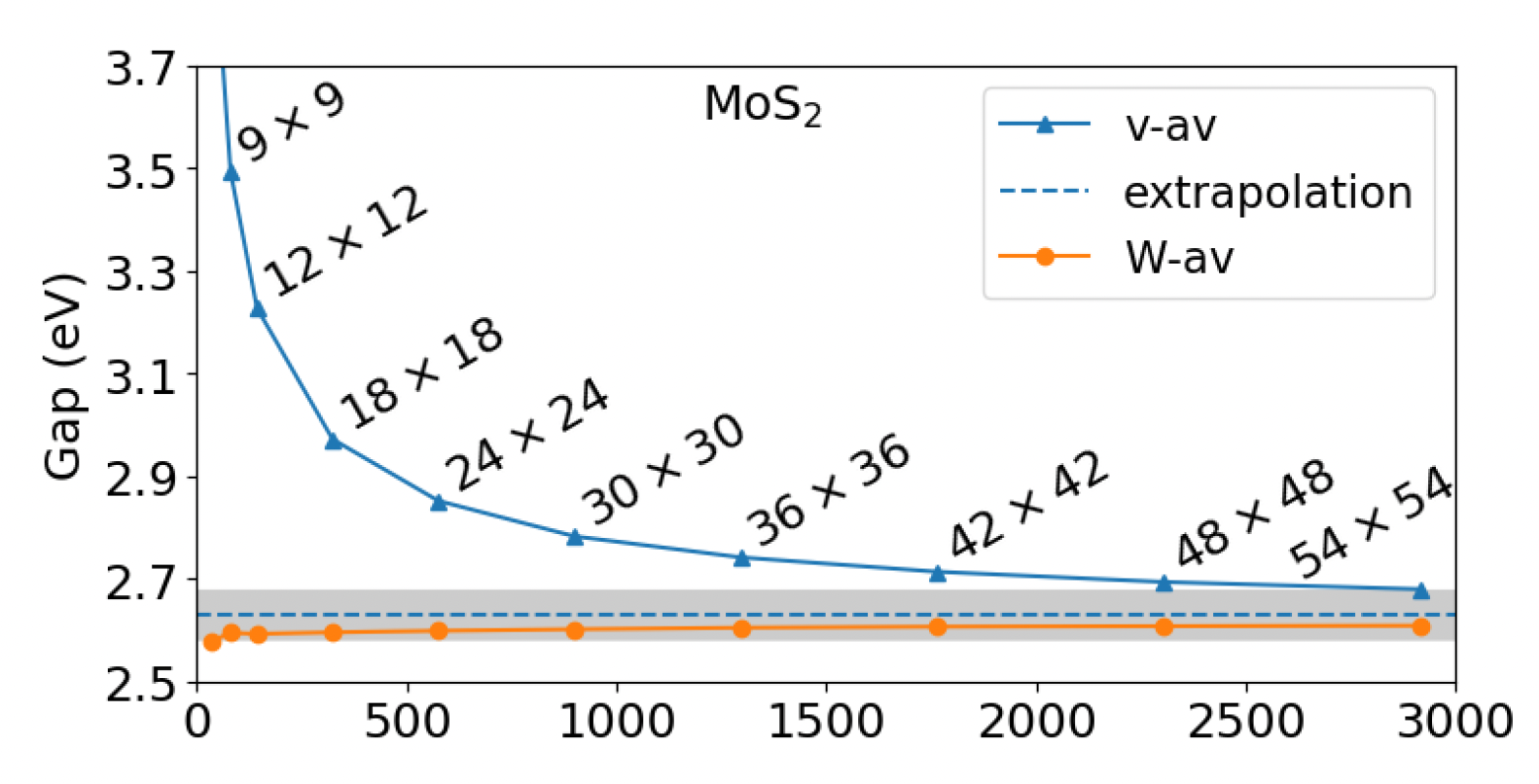
as the dielectric function [math]\displaystyle{ \epsilon_{00} }[/math] goes as q around q=0, matching the 1/q behavior of the Coulomb potential.
To solve this issue, it has been developed a method specific for 2D systems that performs the integration of [math]\displaystyle{ \epsilon_{0 0}(\mathbf{q}) \ v(\mathbf{q}) }[/math] rather than only of [math]\displaystyle{ v(\mathbf{q}) }[/math] when computing the correlation part of self-energy.
Details of this method can be found in the paper Efficient GW calculations in two-dimensional materials through a stochastic integration of the screened potential. You can activate the RIM-W algorithm adding a further flag to your input:
yambo -F gw_ppa.in -p p -r -rw
In your input three further lines should have appeared:
... rim_cut # [R] Coulomb potential RandQpts=1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components RIM_W RandGvecW= 15 RL rimw_type="semiconductor" ...
The variable RandGvecW defines the number of G vectors to integrate W numerically. RandGvecW must be always smaller than the size of the [math]\displaystyle{ \chi }[/math] matrix.
Now repeat the computation again using the RIM-W algorithm.
yambo -F gw_ppa.in -J 80b_10Ry_rimw
How much has the band gap changed ?
Step 2: GW parallel strategies
For this part of the tutorial, we will see how to use a parallel strategy on Yambo. As a test calculation, we compute the full band structure on a larger number of bands with respect the previous calculation.
Differently to the approach used up to now, we will not work interactively but rather we will submit a job script as is commonly done when using Yambo on clusters. So, now exit the interactive mode and in the login node access the folder:
cd $CINECA_SCRATCH/YAMBO_TUTORIALS/MoS2_2Dquasiparticle_tutorial/02_GW_parallel
Here, inspect the input gw.in. You should see we compute a much larger number of quasi-particles:
... %QPkrange # [GW] QP generalized Kpoint/Band indices 1|7|13|17| % ...
For this part of the tutorial, we will be using the slurm submission script job_parallel.sh, which is available in the calculation directory. If you inspect it, you will see that the script adds additional variables to the yambo input file. These variables control the parallel execution of the code:
DIP_CPU= "1 $ncpu 1" # [PARALLEL] CPUs for each role DIP_ROLEs= "k c v" # [PARALLEL] CPUs roles (k,c,v) DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles X_and_IO_CPU= "1 1 1 $ncpu 1" # [PARALLEL] CPUs for each role X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v) X_and_IO_nCPU_LinAlg_INV= 1 # [PARALLEL] CPUs for Linear Algebra X_Threads= 0 # [OPENMP/X] Number of threads for response functions SE_CPU= " 1 $ncpu 1" # [PARALLEL] CPUs for each role SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b) SE_Threads= 0 # [OPENMP/GW] Number of threads for self-energy
The keyword DIP refers to the calculations of the screening matrix elements (also called “dipoles”) needed for the screening function, X is the screening function (it stands for χ since it is a response function), SE the self-energy.
These three sections of the code can be parallelised independently.
The [PARALLEL] variables refer to MPI tasks, instead the threads are used for [OPENMP] parallelisation.
We start by calculating the QP corrections using only the MPI tasks and a single openMP thread. Therefore, create the submission script as:
#!/bin/bash
#SBATCH --nodes=1
#SBATCH --ntasks-per-node=2
#SBATCH --cpus-per-task=1
#SBATCH --partition=m100_sys_test
#SBATCH --qos=qos_test
#SBATCH --reservation=s_tra_yambo
#SBATCH --time=0:30:00
#SBATCH --account=tra23_Yambo
#SBATCH --mem=230000MB
#SBATCH --job-name=rutile
#SBATCH --error=err.job-%j
#SBATCH --output=out.job-%j
# load yambo and dependencies
module purge
module load hpc-sdk/2022--binary
module load spectrum_mpi/10.4.0--binary
export PATH=/m100_work/tra23_Yambo/softwares/YAMBO/5.2-cpu/bin:$PATH
export OMP_NUM_THREADS=${SLURM_CPUS_PER_TASK}
# info
ncpu=${SLURM_NTASKS}
nthreads=${OMP_NUM_THREADS}
label=MPI${ncpu}_OMP${nthreads}
jdir=run_${label}
cdir=run_${label}.out
# Update input file
filein0=gw.in # Original file
filein=gw_${label}.in # New file
cp -f $filein0 $filein
cat >> $filein << EOF
DIP_CPU= "1 $ncpu 1" # [PARALLEL] CPUs for each role
DIP_ROLEs= "k c v" # [PARALLEL] CPUs roles (k,c,v)
DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles
X_and_IO_CPU= "1 1 1 $ncpu 1" # [PARALLEL] CPUs for each role
X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v)
X_and_IO_nCPU_LinAlg_INV=1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set)
X_Threads= 0 # [OPENMP/X] Number of threads for response functions
SE_CPU= "1 $ncpu 1" # [PARALLEL] CPUs for each role
SE_ROLEs= "q qp b" # [PARALLEL] CPUs roles (q,qp,b)
SE_Threads= 0 # [OPENMP/GW] Number of threads for self-energy
EOF
# run yambo
mpirun -n $ncpu yambo -F $filein -J ${jdir} -C $cdir
and submit the job
sbatch job_parallel.sh
This will create a new input file and run it. The calculation databases and the human-readable files will be put in separate directories. Check the location of the report r-* file and the log l-* files, and inspect them while the calculation runs (it should take a couple of minutes).
For simplicity you could just type
tail -f run_MPI8_OMP1.out/LOG/l-*_CPU_1
to monitor the progress in the master thread (Ctrl+C to exit). As you can see, the run takes some time, even though we are using minimal parameters.
On a cluster like m100, to activate the full potential of the machine, it is useful to activate OpenMP threads by modifying cpus-per-task in the submission file. The product of the number of OpenMP and MPI tasks is equal to the total number of CPUs.
Therefore, we can distribute 8 cpus with 4 MPI tasks and then use 2 OpenMP threads:
#!/bin/bash #SBATCH --nodes=1 #SBATCH --ntasks-per-node=4 #SBATCH --cpus-per-task=2
Actually, we don’t need to change the related openMP variables for the yambo input, since the value 0 means “use the value of OMP_NUM_THREADS” and we have now set this environment variable to 2 via our script. Otherwise, any positive number can directly specify the number of threads to be used in each section of the code.
DIP_Threads= 0 # [OPENMP/X] Number of threads for dipoles ... X_Threads= 0 # [OPENMP/X] Number of threads for response functions ... SE_Threads= 0 # [OPENMP/GW] Number of threads for self-energy
You can try to run this calculation and check if it is faster than the pure MPI one from before. In general, you expect to a massive gain with OpenMP if you are already close to an efficient MPI scaling
You can also try any other thread combinations including the pure OpenMP scaling, and compare the timings.
In real-life calculations running on a large number of cores, it may be a good idea to adopt a hybrid approach. The most efficient scaling can depend both on your system and on the HPC facility you’re running on.
In general, OpenMP can help lower memory requirements within a node. You can try to increase the OpenMP share of threads if getting Out Of Memory errors.
Step 3: Running on GPU
For this part of the tutorial, we will repeat the calculation of before, making use of gpus.
So now move to:
02_GW_gpu
Here we are using yet another capability of yambo: running on GPUs instead of CPUs. This usually leads to extreme speedups in the calculations. Fortunately, the m100 cluster also has some GPU nodes! So now let us have a look at the submission script:
vim gpu_job.sh
#!/bin/bash #SBATCH --nodes=1 #SBATCH --ntasks-per-node=2 #SBATCH --cpus-per-task=1 #SBATCH --gres=gpu:4
each GPU node contains four GPUs (--gres=gpu:4). In yambo, each GPU corresponds to a single MPI task, therefore we have still the total number of tasks equal to 8. OpenMP threading is allowed - but not too much, otherwise we lose efficiency. Here in fact, we are not using OpenMP so export OMP_NUM_THREADS=1.
In addition, you will see that in order to run on GPUs we are now using a different executable than before, obtained with a GPU-specific compilation of the code.
module purge module load hpc-sdk/2022--binary spectrum_mpi/10.4.0--binary export PATH=/m100_work/tra23_Yambo/softwares/YAMBO/5.2-gpu/bin:$PATH
In general, the gpu compilation might be different on your machine, or the executable may be the same with no need to load an additional modules. In conclusion, we are running over 4 GPU cards, distributed with 2 MPI tasks, and using 1 thread.
The calculation should faster, about 2 minutes instead of 2 min and 30s with a purely CPU calculation. The gain can become even greater in larger systems. You can have a look at the results collected in folder MPI2_OMP1. The quasiparticle corrections are stored in human-readable form in the file MPI2_OMP1.out/o-GW_bnds.qp, and in netCDF format in the quasiparticle database MPI2_OMP1/ndb.QP.