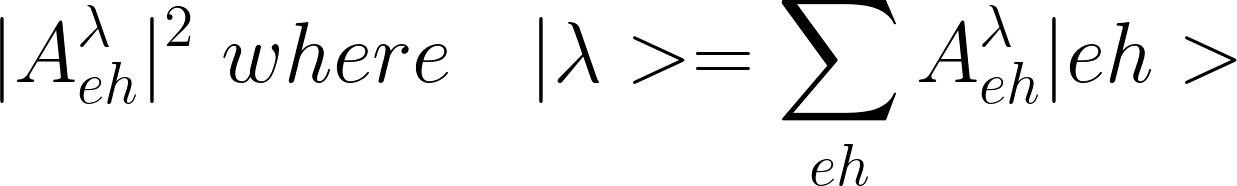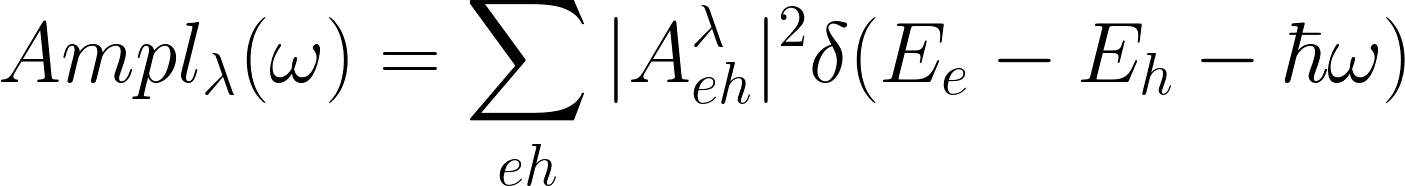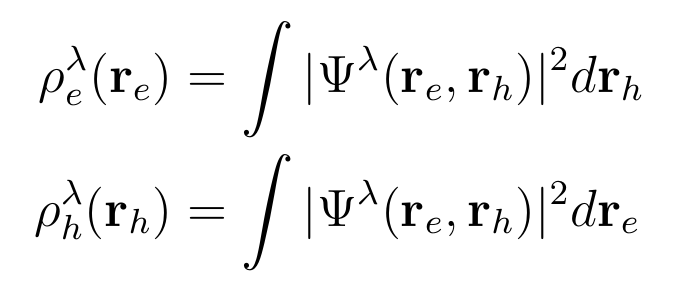How to analyse excitons - ICTP 2022 school

From The Yambo Project
Revision as of 17:58, 28 March 2021 by Myrta (talk | contribs)
Jump to navigation Jump to search

In this tutorial you will learn how to:

  • analyze an optical spectrum obtained from BSE in terms of excitonic energies and composition
  • look at the spatial distribution of the exciton

This is demonstrated for 3D hBN, for which you should have obtained the needed data from previous calculations.


Prerequisites

Previous modules

You will need:

  • The SAVE databases for 3D hBN
  • The 3D_BSE directory containing the ndb.BS_diago* databases for 3D hBN
  • ypp executable
  • xcrysden or VESTA executables
  • gnuplot executable

All the databases required for this tutorial should be in the YAMBO_TUTORIALS/hBN/ directory.

List the excitonic energies

First, we will obtain the list of all the exciton energies (that is the eigenvalues of the two-particle Hamiltonian) sorted both by energies and oscillator strength.

To read this information from the Yambo databases produced in this previous step, we use the Yampo pre- and post-processing utility ypp.

Type: 

$ ypp -J 3D_BSE -e s 1

This instructs the code to list the excitons for the q-index = 1 (optical limit q=0).

The results are output in the files o-3D_BSE.exc_qpt1_E_sorted and o-3D_BSE.exc_qpt1_I_sorted. They report the energies of the excitons and their oscillator strengths. The strengths are normalised to the largest strength. Thus in the list, the brightest exciton has strength 1. In o-3D_BSE.exc_qpt1_E_sorted the exciton energies are sorted by energy (lower to higher), in o-3D_BSE.exc_qpt1_I_sorted by the oscillator strength (larger to smaller).

Strengh.png

Inspect 'o-3D_BSE.exc_qpt1_E_sorted: The exciton with the lowest energy (3.54 eV) is doubly degenerate. The second-lowest is also doubly degenerate and is the brightest (oscillator strength of 1). The latter exciton is the one responsible for the largest peak in the optical absorption plots of the previous tutorials.

To visualize these results, we plot them: 

$ gnuplot
gnuplot> set style line 2 lc rgb 'black' pt 7   # circle
gnuplot> plot 'o-3D_BSE.exc_qpt1_E_sorted' with points ls 2 title 'Strengths'
ExcWeights3DhBN.png

<---!Warning: the convergence of these results with different k-points grids is mandatory! --->

Calculate the exciton oscillator strength and amplitude

We can now analyze the excitons in terms of single-particle states: which electronic transitions are the most relevant? In order to do that, create the appropriate input with 

$ ypp -F ypp_AMPL.in -J 3D_BSE -e a 1

Suppose you wish to analyze the first 4 excitons (i.e., the first 2 doubly-degenerate excitons). Then, change this line as: 

States= "1 - 4"              # Index of the BS state(s)

Close the input and run ypp 

$ ypp -F ypp_AMPL.in -J 3D_BSE

$ ls  o*exc*at*
o-3D_BSE.exc_qpt1_amplitude_at_1 o-3D_BSE.exc_qpt1_weights_at_1 ...

For an exciton [math]\displaystyle{ |\lambda\gt }[/math] , o-3D_BSE.exc_qpt1_weights_at_* report the Weights

Weights.png

and o-3D_BSE.exc_qpt1_amplitude_** report the amplitudes

Ampl.png

Open the file o-3D_BSE.exc_weights_at_3 

# Band_V          Band_C          Kv-q ibz        Symm_kv         Kc ibz          Symm_kc         Weight          Energy
#    
  7.00000000      10.0000000      14.0000000      2.00000000      14.0000000      2.00000000     0.395135850      4.35248947   
  7.00000000      10.0000000      14.0000000      1.00000000      14.0000000      1.00000000     0.394993663      4.35248947   
  8.00000000      9.00000000      14.0000000      2.00000000      14.0000000      2.00000000     0.391943455      4.35241365   
  8.00000000      9.00000000      14.0000000      1.00000000      14.0000000      1.00000000     0.391800284      4.35241365   
  7.00000000      10.0000000      13.0000000      2.00000000      13.0000000      2.00000000     0.745555162E-1   4.81094742   
  7.00000000      10.0000000      13.0000000      1.00000000      13.0000000      1.00000000     0.745274872E-1   4.81094742   
  8.00000000      9.00000000      13.0000000      2.00000000      13.0000000      2.00000000     0.739243180E-1   4.81087065   
  8.00000000      9.00000000      13.0000000      1.00000000      13.0000000      1.00000000     0.738964081E-1   4.81087065

The third exciton is mostly composed of single-particle transitions from VBM to CBM at point H (last k-point of the grid, number 14) of the 3D hexagonal Brillouin zone, with contributions also coming from point K (number 13). All the contributions weighing less than 5% are not shown by default. Recall from the previous analysis that exciton states 3 and 4 (degenerate) are the optically active ones.

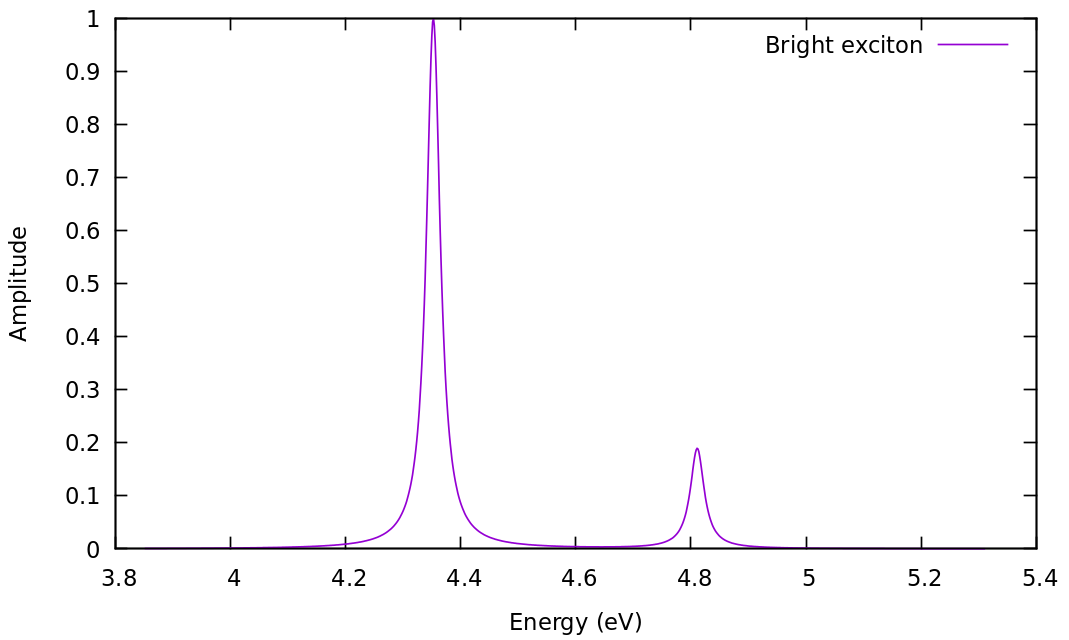
We can now plot the amplitude of the bright exciton: 

$ paste o-3D_BSE.exc_qpt1_amplitude_at_3 o-3D_BSE.exc_qpt1_amplitude_at_4 > o-3D_BSE.exc_qpt1_amplitude_at_3_4
$ gnuplot
gnuplot> set xlabel 'Energy (eV)' 
gnuplot> set ylabel 'Amplitude' 
gnuplot> p 'o-3D_BSE.exc_qpt1_amplitude_at_3_4' u 1:($2+$4)/2 w l t 'Bright exciton'
ExcAmp3DhBN.png

Recall that while this plot is related to the peaks in the optical absorption spectrum, it lacks the coupling with the external field, which is encoded in the dipole matrix elements.

Plot the exciton spatial distribution

To see the spatial character of the exciton, YPP writes the exciton spatial distribution, e.g., the probability to find the electron when the hole is fixed in a given position. Different output formats can be selected and to obtain 1D, 2D, and 3D plots.

Create the input and change the various parameters as shown below. 

$ ypp -F ypp_WF.in -J 3D_BSE -e w

excitons                     # [R] Excitons
wavefunction                 # [R] Wavefunction
Format= "x"                  # Output format [(c)ube/(g)nuplot/(x)crysden]
Direction= "123"               # [rlu] [1/2/3] for 1d or [12/13/23] for 2d [123] for 3D
FFTGvecs=  30        Ry    # [FFT] Plane-waves
States= "3 - 3"              # Index of the BS state(s)
Degen_Step=   0.0100   eV    # Maximum energy separation of two degenerate states
% Cells
 5 | 5 | 1 |                             # Number of cell repetitions in each direction (odd or 1)
%
% Hole
2.35800028 | 1.36139178 | 7.08835602 # [cc] Hole position in unit cell (positive)
%

One of the parameters, Cells, is the size of the cell where the exciton will be visualised. Note that if the k-grid of the BSE simulation is XxYxZ, then the exciton has an induced fictitious periodicity for every XxYxZ cells of the simulation. For hBN, this is not a problem because the exciton is strongly localized, but in other systems, where excitons are more delocalized, it may b necessary to use very large k-grids for the BSE calculation.

Also notice that, because of the value of Degen_Step, the code will automatically recognize and merge the degenerate excitons 3 and 4: you will see this in the log file.

Finally: how did we know at which coordinate to place the hole? It's best placed in the position where the valence electrons contributing to the exciton are localised. In the case of hBN, they are on the nitrogen atoms. We can obtain the Cartesian coordinates of these atoms from our previously generated o-3D_BSE.exc_qpt1_E_sorted file: 

# Atom 1 with Z 5 [cc]:  2.35800028      1.36139178      0.00000000   
# Atom 2 with Z 5 [cc]: -2.35800028     -1.36139178      6.08835602   
# Atom 1 with Z 7 [cc]: -2.35800028     -1.36139178      0.00000000   
# Atom 2 with Z 7 [cc]:  2.35800028      1.36139178      6.08835602

We take the positive values of the nitrogen(Z=7, last line) and shift the vertical position of the hole from 6.088 to 7.088 so that the hole does not end up in the center of the atom (and therefore, possibly in a node of the wave function).

Now close the input and run ypp 

$ ypp -F ypp_WF.in -J 3D_BSE

After it's finished, we can visualise with xcrysden or with VESTA: 

$ xcrysden --xsf o-3D_BSE.exc_qpt1_3d_3.xsf

$ VESTA o-3D_BSE.exc_qpt1_3d_3.xsf
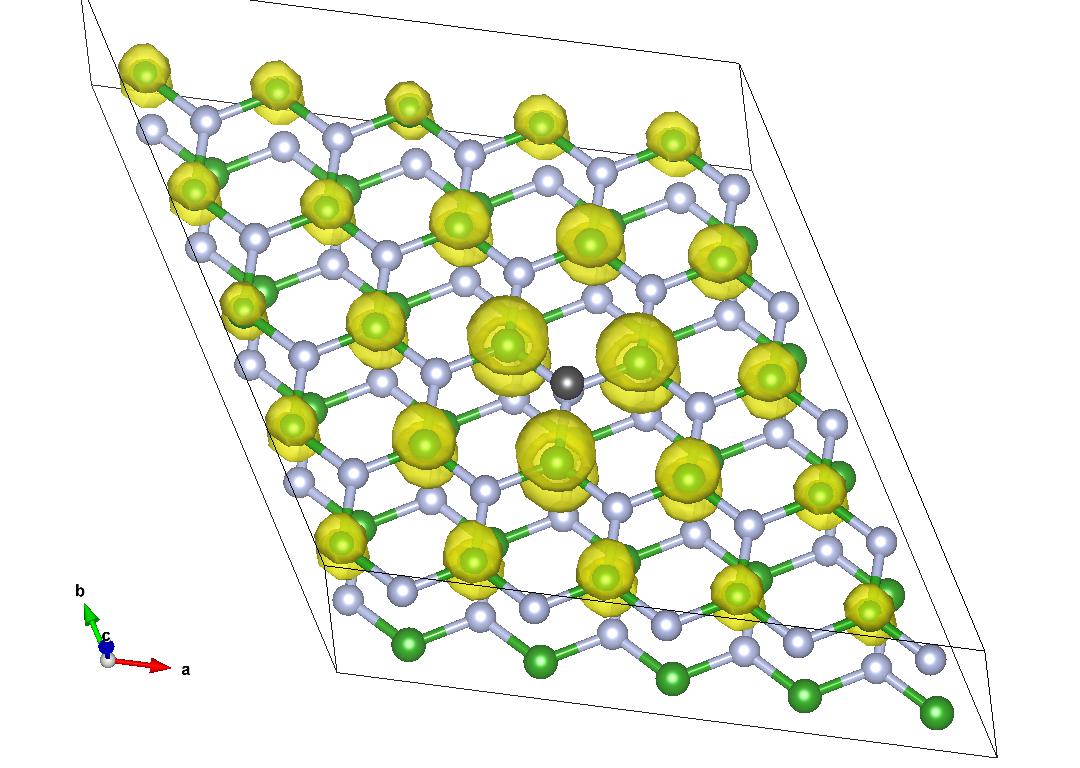
ExcWF3DhBN.jpg

We notice that the electron is completely confined on the boron atoms and on the same layer of the hole. For comparison, see for example ref. [1].

Plot electron/hole average density (only in Yambo 5.x)

Another way to analyze excitons, it is the possibility to plot the average electron/hole densities defined as:

Electron hole density.png

to generate the corresponding input just type 

ypp -F ypp_WF.in -e w -avehole

and choose the exciton you want to plot. The electron/hole average densities correspond to generalized valence/conduction orbitals for a given exciton. They are interesting in particular for molecular crystals because they allow distinguishing charge-transfer versus Frenkel excitons, from the relative position of the electron/hole densities.

If you want to see an example of hole/electron density of excitons please have a look to ref. [2].

Summary

From this tutorial you've learned:

  • How sort excitonic states by energy and intensity
  • Analyse their composition in reciprocal space and in terms of single-particle transitions
  • Visualize the exciton wave function in real space

Navigate

  1. ↑ Huge Excitonic Effects in Layered Hexagonal Boron Nitride, B. Arnaud et al., preprint ArXiv
  2. ↑ Strongly Bound Excitons in Metal-Organic Framework MOF-5: A Many-Body Perturbation Theory Study, A. R. Kshirsagar et al., preprint ChemRxiv
Retrieved from "https://wiki.yambo-code.eu/wiki/index.php?title=How_to_analyse_excitons_-_ICTP_2022_school&oldid=4494"