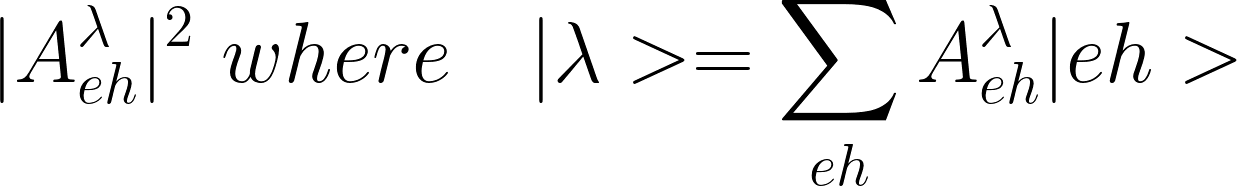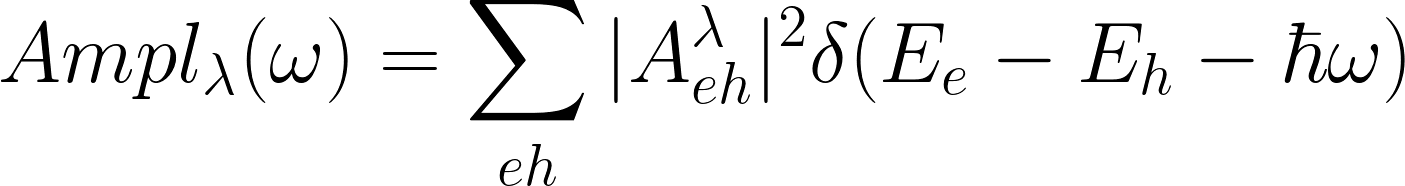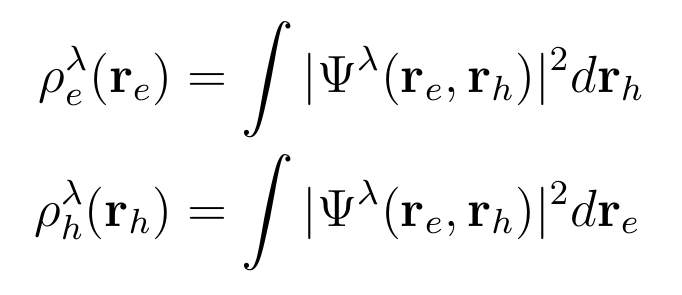How to analyse excitons - ICTP 2022 school

In this tutorial you will learn (for 3D-hBN) how to:

• analyze a BSE optical spectrum in terms of excitonic eigenvectors and eigenvalues
• look at the spatial distribution of the exciton
• For a similar tutorial focusing on 2D-hBN and including finite-momentum BSE, go to this page.

Prerequisites

Previous modules

• You must have completed the Calculating optical spectra including excitonic effects: a step-by-step guide tutorial

You will need:

• The SAVE databases for 3D hBN
• The ndb.BS_diago* databases for 3D hBN
• ypp executable
• xcrysden executable
• gnuplot executable

YAMBO calculations

If you have completed the tutorials on 3D hBN you should have all the databases required to do this tutorial in your YAMBO_TUTORIALS/hBN/SAVE and YAMBO_TUTORIALS/hBN/3D_BSE directories.

$ ls ./SAVE
ndb.gops ndb.kindx ns.db1 ns.kb_pp_pwscf_fragment_1 ....

$ ls ./3D_BSE
ndb.BS_Q1_CPU_0 ndb.BS_diago_Q1 ndb.dip_iR_and_P_fragment_1 ndb.em1s_fragment_1 ...

Sort the excitonic eigenvalues

We are now going to use ypp to post-process our BSE results. First, type

$ ypp -J 3D_BSE -e s 1

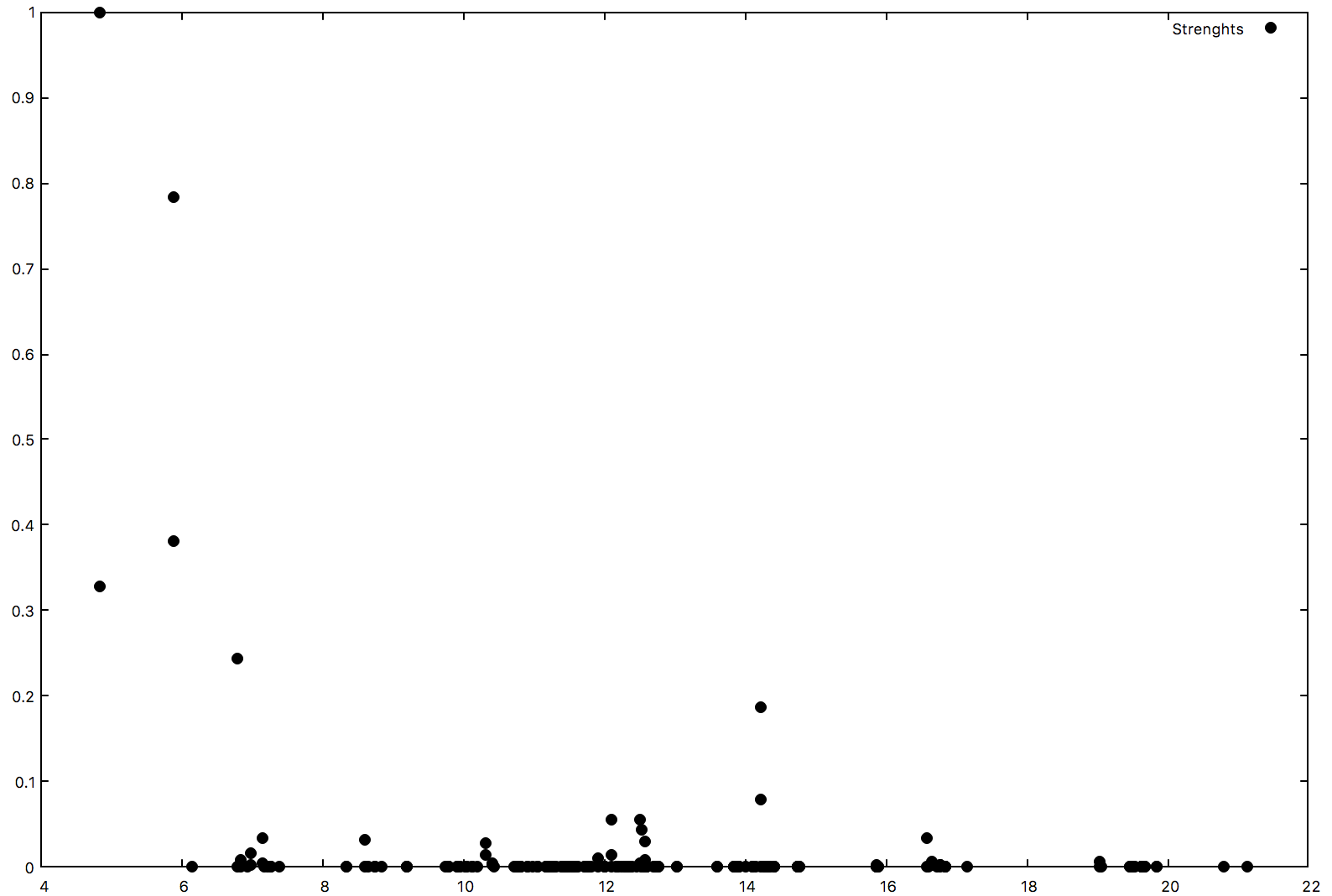
which means that we are sorting the excitons for the q-index = 1 (optical limit q=0). The new generated file o-3D_BSE.exc_qpt1_E_sorted (along with o-3D_BSE.exc_qpt1_I_sorted ) reports the energies of the excitons and their Dipole Oscillator Strengths sorted by Energy (Intensity).

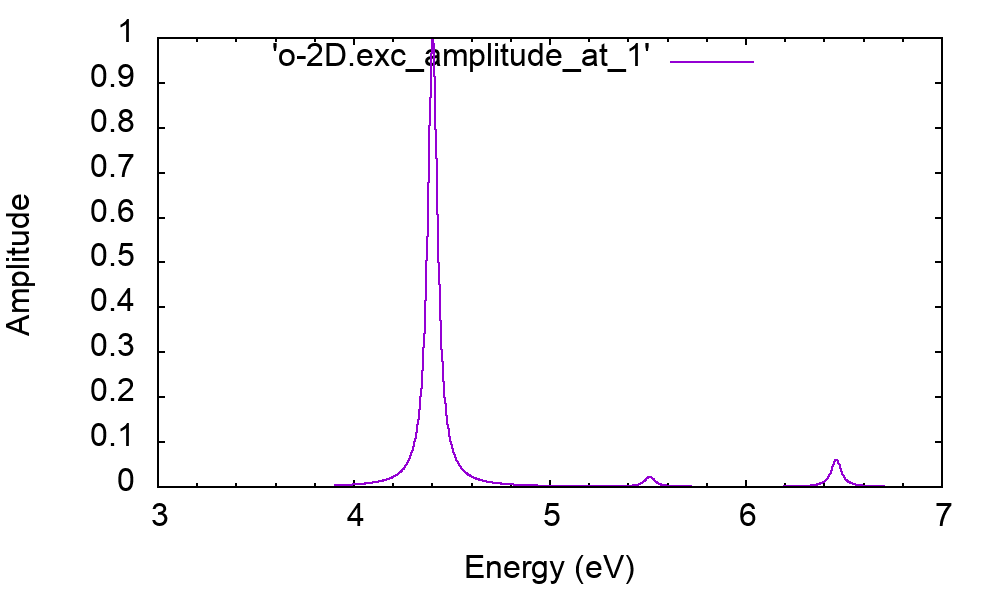
Open the first file and look inside. The first exciton is doubly degenerate at the energy of 3.54 eV, and the second one - also doubly degenerate - has the highest strength (normalized to 1). The latter exciton is the one appearing as the major peak in the optical absorption plots of the previous tutorials

Or you can make a plot

$ gnuplot

gnuplot> set style line 2 lc rgb 'black' pt 7 # circle gnuplot> plot 'o-3D_BSE.exc_qpt1_E_sorted' with points ls 2 title 'Strengths'

Attention: the convergence of these results with different k-points grids is mandatory!

Calculate the exciton oscillator strenght and amplitude

We can now analyze the excitons in terms of single-particle states, to do that create the appropriate input

$ ypp -F ypp_AMPL.in -J 2D_WR_WC -e a 1 

Suppose you wish to analyze the first 5 excitons then change this line as:

States= "1 - 5"              # Index of the BS state(s)

Close the input and run ypp

$ ypp -F ypp_AMPL.in -J 2D_WR_WC

$ls  o*exc*at*
o-2D_WR_WC.exc_qpt1_amplitude_at_1 o-2D_WR_WC.exc_qpt1_weights_at_1 ...

For an exciton [math]\displaystyle{ |\lambda\gt }[/math] , o-2D_WR_WC.exc_qpt1_weights_at_* report the Weights

and o-2D_WR_WC.exc_qpt1_amplitude_** report the amplitudes

Open the file o-2D_WR_WC.exc_weights_at_1

#  Band_V     Band_C     K  ibz     Symm.      Weight     Energy
#
 4.000000   5.000000   7.000000   2.000000   0.922095   4.401093
 4.000000   5.000000   7.000000   1.000000   0.922086   4.401093
The first exciton is  essentially done of only single particle transitions from VBM to CBM at K (last k-point of the grid).

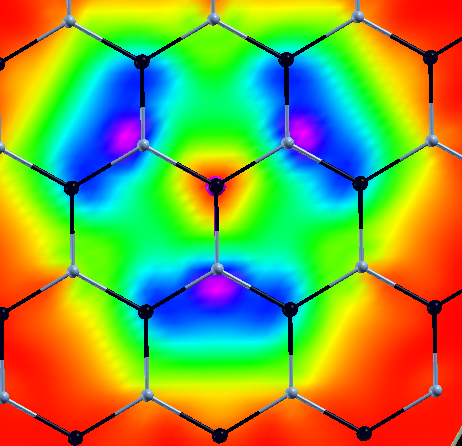
Plot the exciton spatial distribution

To see the spatial character of the exciton YPP writes the exciton spatial distribution, in other words the probability to find the electron somewhere in the space when the hole is fixed in a give position. Different output formats can be selected and 1D,2D,3D plots done. Create the input and change the size of the cell where to see the exciton. Note that If the k-grid of the BSE simulation is a NxNx1 the exciton has an induced fictitious periodicity every Nx Nx1 Cell of the simulation. For hBN-2D this is not a problem because the exciton is strongly localized but in other systems with more delocalized excitons to look at the real exciton size it is necessary to use very large k-grids in the BSE

$ ypp -F ypp_WF.in -J 2D_WR_WC  -e w  1

excitons                     # [R] Excitons
wavefunction                 # [R] Wavefunction
Format= "x"                  # Output format [(c)ube/(g)nuplot/(x)crysden]
Direction= "12"               # [rlu] [1/2/3] for 1d or [12/13/23] for 2d [123] for 3D
FFTGvecs=  3951        RL    # [FFT] Plane-waves
States= "1 - 1"              # Index of the BS state(s)
Degen_Step=   0.0100   eV    # Maximum energy separation of two degenerate states
% Cells
 5 | 5 | 1 |                             # Number of cell repetitions in each direction (odd or 1)
%
% Hole
2.4     | 1.400     | 0.00     |        # [cc] Hole position in unit cell

Close the input and run ypp

$ ypp -F ypp_WF.in -J 2D_WR_WC 

$ xcrysden --xsf o-2D_WR_WC.exc_2d_1.xsf

Plot electron/hole average density (only in Yambo 5.x)

Another way to analyze excitons, it is the possibility to plot the average electron/hole densities defined as:

to generate the corresponding input just type

ypp -F ypp_WF.in -e w -avehole

and choose the exciton you want to plot. The electron/hole average densities correspond to generalized valence/conduction orbitals for a given exciton. They are interesting in particular for molecular crystals because they allow distinguishing charge-transfer versus Frenkel excitons, from the relative position of the electron/hole densities.

If you want see an example of hole/electron density of excitons please have a look to ref. .

Interpolate exciton dispersion (only in Yambo 5.x)

Starting from Yambo 5.x it is possible to calculate excitons at finite momentum q. The momentum can be specified with the variable

%BSEQptR
 iq_start | iq_end |                             # [BSK] Transferred momenta range
%

where iq_start and iq_end is the first and last index of momentum in the irreducible Brillouin zone (IBZ). You can find the list of q-vectors in the r_setup report. If you calculate the BSE for all q-points of the IBZ, then you can interpolate exciton dispersion along any direction of the full Brillouin zone(BZ) using the interpolation scheme of ref. , by doing:

ypp -e i 

and then setting:

excitons                         # [R] Excitonic properties
interpolate                      # [R] Interpolate
States= "1 - 4"                  # Index of the BS state(s)
INTERP_mode= "BOLTZ"                # Interpolation mode (NN=nearest point, BOLTZ=boltztrap aproach)
% INTERP_Grid
 -1 |-1 |-1 |                             # Interpolation BZ Grid 
%
#PrtDOS                          # Print Exciton Density of States
BANDS_steps= 100                 # Number of divisions
cooIn= "rlu"                     # Points coordinates (in) cc/rlu/iku/alat
cooOut= "rlu"                    # Points coordinates (out) cc/rlu/iku/alat
%BANDS_kpts                      # K points of the bands circuit
0 | 0 | 0 |
0.333333333333333 | 0.33333333333333 | 0 | 
%

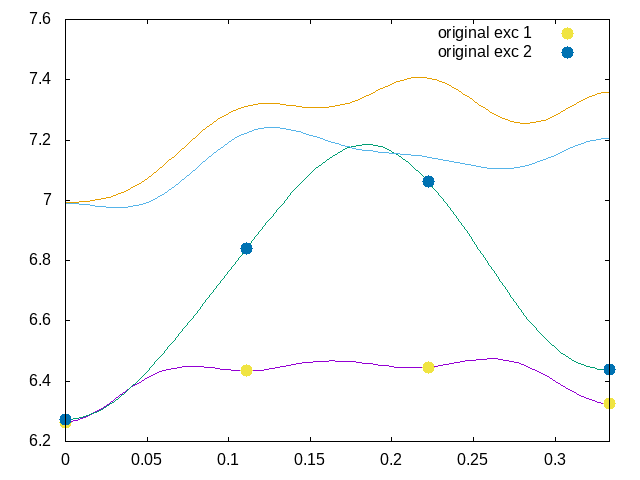
Running ypp, it will interpolate the first 4 excitons energies on 100 points along with the line Gamma->K. If you plot the output file "o.excitons_interpolated", you can compare the interpolated results with the original points calculated in the BSE, that are available in the report "r_excitons_interpolate", and you get something like:

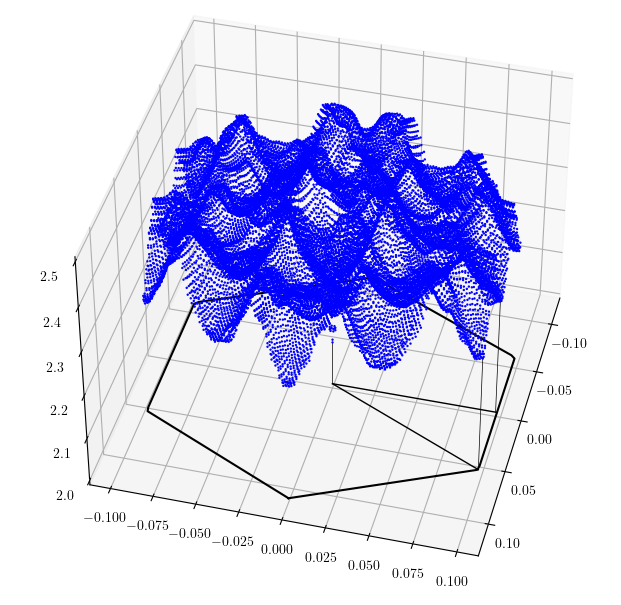
It is also possible to interpolate excitons on a given regular grid by setting INTERP_Grid, for example in the figure below we interpolate the dispersion of the lowest exciton in MoS₂ calculated on a 39x39x1 and interpolated in a 117x117x1 grid in all the Brillouin zone:

Finally if you turn on the flag PrtDOS the code calculate the excitonic density of states on the excitons interpolated on the regular grid given by INTERP_Grid.