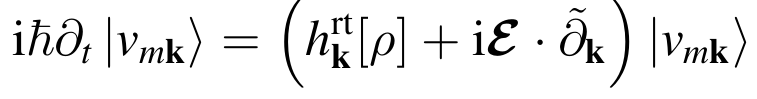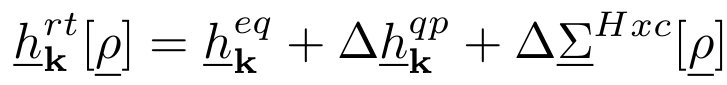Real time Bethe-Salpeter Equation (TDSE)
Background
In Yambo we combined static screened self-energy derived by means of Non-equilibrium Green's function with Modern Theory of Polarization (Ref. [1] and [2])
where the Hamiltonian is obtained from Green's function theory and is written as:
where [math]\displaystyle{ \rho_0 }[/math] and [math]\displaystyle{ \gamma_0 }[/math] are the density and the single-particle density matrix at equilibrium, [math]\displaystyle{ \Sigma^{COHSEX} }[/math] is the COHSEX self-energy and [math]\displaystyle{ V^H }[/math] is the Hartree potential. This Hamiltonian corresponds to a real-time version of the Bethe-Salpeter Equation[1]. Then the polarization is calculated by means of Berry's phase formulation as it has been shown in the Real time approach to linear response (TDSE) tutorial.
Prerequisites
You need yambo_nl and ypp_nl compiled in double precision for this tutorial. The DFT inputs and yambo databases can be found here: .
Real time Bethe-Salpeter Equation
This tutorial will show how to perform a simple real-time BSE calculation with Yambo on hBN monolayer. Use the same DFT inputs of the previous tutorial, but increase the number of k-points to 10 10 1 in such a way to have converged exciton. Follow the first 6 steps of the Real time approach to linear response using TDSE. Then generate the input file to calculate the collisions (see appendix of Ref. [2]) use the command : yambo_nl -b -e -v h+sex. The flag -b will tell the code to calculate the dielectric constant that is required for the screened interaction.
em1s # [R Xs] Static Inverse Dielectric Matrix collisions # [R] Eval the extended Collisions dipoles # [R ] Compute the dipoles DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions RT_Threads=0 # [OPENMP/RT] Number of threads for real-time Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc % BndsRnXs 1 | 40 | # [Xs] Polarization function bands % NGsBlkXs= 1000 mHa # [Xs] Response block size % DmRngeXs 0.10000 | 0.10000 | eV # [Xs] Damping range % % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field % % COLLBands 4 | 5 | # [COLL] Bands for the collisions % HXC_Potential= "HARTREE+SEX" # [SC] SC HXC Potential HARRLvcs= 1000 mHa # [HA] Hartree RL components EXXRLvcs= 1000 mHa # [XX] Exchange RL components CORRLvcs= 1000 mHa # [GW] Correlation RL components
With this input, we calculate the HARTREE and SEX collisions integrals. Notice that the HARTREE term in principle can be calculated on the fly, but in this way it is more efficient especially for the non-linear response.
Here one has to converge the cutoff for the Hartree and the Screened Exchange, usually, around 5000 mHa it is a good value, in this example, I put 1000 mHa to speed up calculations. The collisions bands COLLBands have to be the same number of bands you want to use in the linear/nonlinear response. Run this calculation, it will take 5 minutes on a serial PC.
Then you generate the input for the linear response yambo_nl -u -V qp :
nloptics # [R NL] Non-linear optics DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles NL_Threads=0 # [OPENMP/NL] Number of threads for nl-optics % NLBands 4 | 5 | # [NL] Bands % NLverbosity= "low" # [NL] Verbosity level (low | high) NLstep= 0.0100 fs # [NL] Real Time step length NLtime= 55.00000 fs # [NL] Simulation Time NLintegrator= "CRANKNIC" # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "SEX" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.200000 | 8.000000 | eV # [NL] Energy range % NLEnSteps= 1 # [NL] Energy steps NLDamping= 0.10000 eV # [NL] Damping #UseDipoles # [NL] Use Covariant Dipoles (just for test purpose) #FrSndOrd # [NL] Force second order in Covariant Dipoles #EvalCurrent # [NL] Evaluate the current HARRLvcs= 1017 RL # [HA] Hartree RL components EXXRLvcs= 1074 mHa # [XX] Exchange RL components % ExtF_Dir 0.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor % ExtF_Int= 1000. kWLm2 # [NL ExtF] Intensity ExtF_Width= 0.000000 fs # [NL ExtF] Field Width ExtF_kind= "DELTA" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) ExtF_Tstart= 0.0100 fs # [NL ExtF] Initial Time % GfnQP_E 3.000000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim %
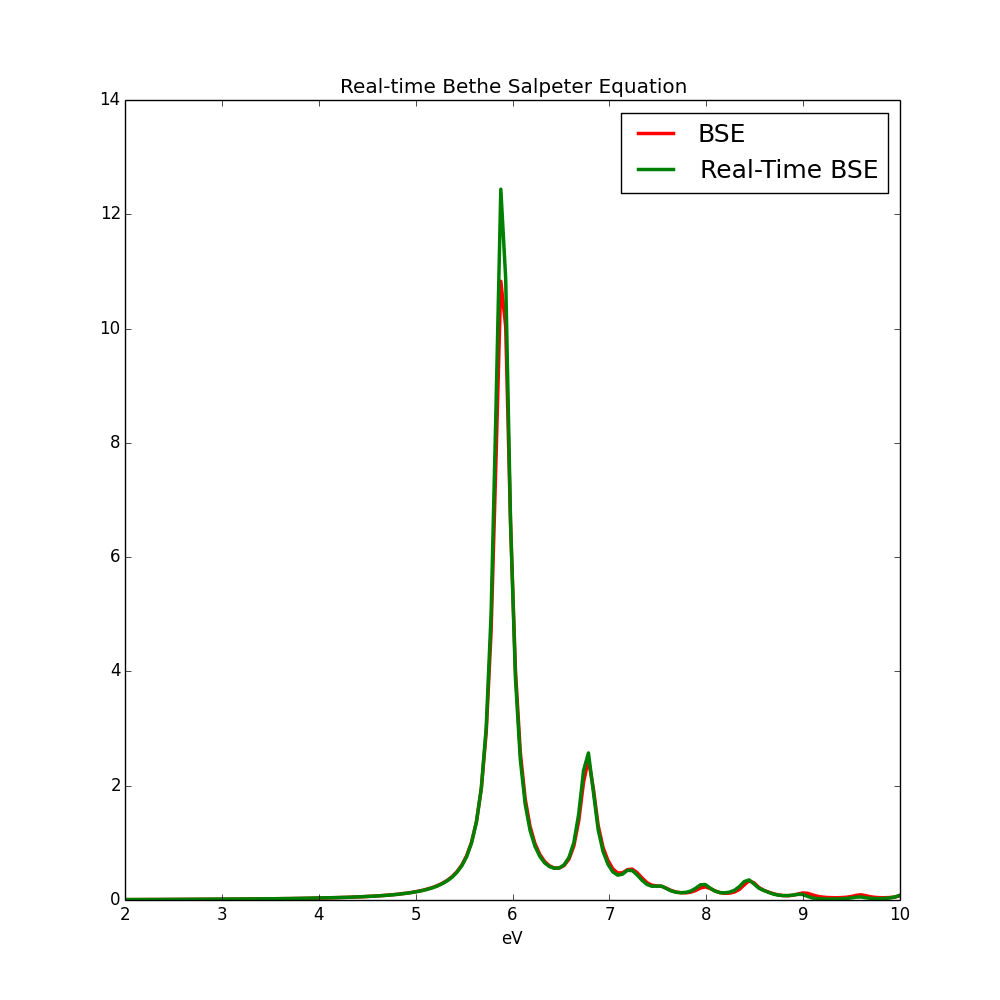
Notice that we introduced a scissor operator (a rigid shift of the conduction bands) of 3.0 eV. In principle, it is possible to perform a G0W0 calculation with Yambo and use the Quasi-particle band structure instead of the rigid shift. Run this calculation and then analyze the result in the same way of linear response tutorial, you will get a nice exciton in hBN, as the one plotted below in the old tutorial. You can repeat the same kind of calculations for the non-linear response.
Notice that in the calculation we decreased the number of G-vectors in the Hartree term, HARRLvcs to speed up the calculation, in case of BN this does not change the result because local field effects are very small in h-BN along the plane.
Now you can analyze the response with ypp as it was done the linear response tutorial and compare with the standard Bethe-Salpeter (input here):
Linear response results can be obtained following the BSE tutorial. Notice that you can use the SEX approximation for the non-linear response too (see the following tutorials on non-linear response).