Correlation effects in the non-linear response
In this tutorial, we will show how to include correlation effects in the Second Harmonic Generation. We start from the tutorial on SHG in AlAs, using the same DFT inputs and parameters. Notice that the tutorials on TD-Hartree, TD-DFT, and TD-DPFT require more computational time, if calculations are too slow you can run in parallel or decrease the number of frequencies in your SHG.
Background
In real-time simulations using TDSE, correlation effects are determined by the choice of the Hamiltonian \( H^{\text{sys}}_{\mathbf k} \) that enters in the equations of motion(EOM).
Yambo can use different models for the system Hamiltonian:
- The independent-particle (IP) model,
[math]\displaystyle{ H^{\text{IP}}_{\mathbf k} \equiv H^{\text{KS}}_{\mathbf k} }[/math]
where [math]\displaystyle{ H^{\text{KS}}_{\mathbf k} }[/math] is the unperturbed KS Hamiltonian and we consider the KS system as a system of independent particles.
- The QP model, $$ H^{\text{QP}}_{\mathbf k} \equiv H^{\text{KS}}_{\mathbf k} + \Delta H_{\mathbf k}. $$ where GW corrections or scissor operator, estimated from the Many-Body Perturbation Theory (ref. [4]), has been applied to the KS eigenvalues. # The RPA model, $$ H^{\text{RPA}}_{\mathbf k} \equiv H^{\text{KS}}_{\mathbf k} + V_h(\mathbf r)[\Delta\rho], $$ The term \( V_h(\mathbf r)[\Delta\rho] \) is the time-dependent Hartree potential and is responsible for the local-field effects originating from system inhomogeneities, and \( \Delta \rho \equiv \rho(\mathbf r;t)-\rho(\mathbf r;t=0) \) is the variation of the electronic density. # The Time Dependent-Density Functional Theory (TD-DFT) model, at present only for LDA or GGA functionals: $$ H^{\text{RPA}}_{\mathbf k} \equiv H^{\text{KS}}_{\mathbf k} + V_h(\mathbf r)[\Delta\rho] + V_{xc}(\mathbf r)[\Delta\rho] $$ The term \( V_{xc}(\mathbf r)[\Delta\rho] \) is the time-dependent exchange-correlation potential. # The Time Dependent-Density Polarization Function Theory (TD-DPFT) model, at present different functionals are implemented in Lumen, for more details see ref. [5]: $$ H^{\text{RPA}}_{\mathbf k} \equiv H^{\text{KS}}_{\mathbf k} + V_h(\mathbf r)[\Delta\rho] + V_{xc}(\mathbf r)[\Delta\rho] -\Omega \mathcal{E}^s(t) \cdot \nabla_{\mathbf k} $$ where \( \mathcal{E}^s(t) \) is the Kohn-Sham macroscopic field (see ref.[5-6]).
Non-linear susceptibilities
During the time evolution the bulk polarization is calculated by means of King-Smith Vanderbilt formula (ref. [7]) and the nonlinear susceptibilities are obtained by inversion of the Fourier matrix as described in ref. [3]: $$ P=P^0 + \chi^{(1)} E + \chi^{(2)} E^2 + \chi^{(3)} E^3 + O(E^4)$$ Notice that the finite broadening in the spectra is obtained by adding a dephasing operator in the original Hamiltonian (ref. [3]).
== References: == # Manifestations of Berry’s phase in molecules and condensed matter, Raffaele Resta, J. Phys.: Condens. Matter, 12,R107–R143(2000) # Dynamics of Berry-phase polarization in time-dependent electric fields, I. Souza, J. Iniguez, and D. Vanderbilt, Phys. Rev. B 69, 085106 (2004) # Nonlinear optics from an ab initio approach by means of the dynamical Berry phase: Application to second- and third-harmonic generation in semiconductors, C. Attaccalite, M. Grüning, Phys. Rev. B, 88, 235113 (2013) # The GW method, F. Aryasetiawan, O. Gunnarsson, Rep. Prog. Phys. 61, 237 (1998) # Dielectrics in a time-dependent electric field: a real-time approach based on density-polarization functional theory, M. Grüning, D. Sangalli, C. Attaccalite, Phys. Rev. B 94, 035149 (2016) # Functional theory of extended Coulomb systems, R. M. Martin and G. Ortiz, Phys. Rev. B 56, 1124 (1997) # Theory of polarization of crystalline solids, R.D. King-Smith, D. Vanderbilt, Phys. Rev. B 47, 1651(R) (1993) # Non-linear response in extended systems: a real-time approach, C. Attaccalite (2017)
Quasi-particle corrections
Quasi-particle correction can be easily introduced in the real-time dynamics by means of a non-local operator that modifies the Kohn-Sham eigenvalues: $$ \Delta \hat H = \sum_{n,\bf k} \Delta_{n,\bf k} |v^0_{n,\bf k}\rangle\langle v^0_{n,\bf k}|. $$ The command to turn on quasi-particle corrections is: "yambo_nl -u -V qp" :
nlinear # [R NL] Non-linear optics
% NLBands
3 | 6 | # [NL] Bands
%
NLintegrator="INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF")
NLLrcAlpha= 0.000000 # [NL] Long Range Correction
% NLEnRange
1.000000 | 5.000000 | eV # [NL] Energy range
%
NLEnSteps= 10 # [NL] Energy steps
NLDamping= 0.150000 eV # [NL] Damping
% ExtF_Dir
1.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor
%
ExtF_kind= "SOFTSIN" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
GfnQPdb= "none" # [EXTQP G] Database
GfnQP_N= 1 # [EXTQP G] Interpolation neighbours
% GfnQP_E
0.900000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim
%
GfnQP_Z= ( 1.000000 , 0.000000 ) # [EXTQP G] Z factor (c/v)
GfnQP_Wv_E= 0.000000 eV # [EXTQP G] W Energy reference (valence)
% GfnQP_Wv
0.00 | 0.00 | 0.00 | # [EXTQP G] W parameters (valence) eV| eV|eV^-1
%
GfnQP_Wc_E= 0.000000 eV # [EXTQP G] W Energy reference (conduction)
% GfnQP_Wc
0.00 | 0.00 | 0.00 | # [EXTQP G] W parameters (conduction) eV| eV|eV^-1
%
All the parameters of this input are the same of the previous tutorial with the only difference that we introduced a scissor operator of 0.9 eV. Notice that it is possible to import also the quasi-particle corrections calculated within the G0W0 approximation by using the flag
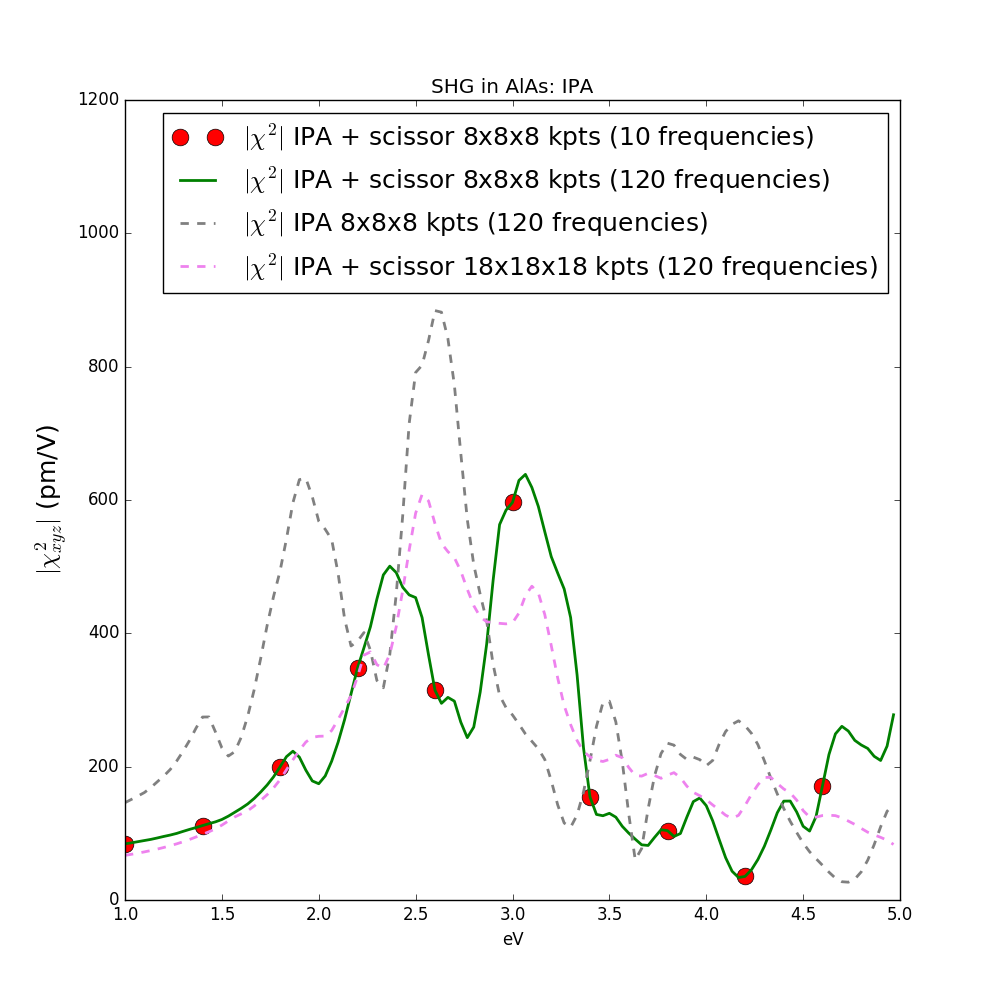
GfnQPdb="E < SAVE/ndb.QP" (see Yambo tutorial on GW for more information). Now you can run lumen and then analyze the results as explained in the previous tutorial. The effect of then scissor-operator is shown in the following figure:
The figure compares results with scissor operator "IPA + scissor" (red dots) with the one obtained in the previous tutorial "IPA". The full converged result is obtained with a 18x18x18 k-point grid and bands between 2 and 10 (violet dashed line). The script and the data to generate this plot can be downloaded here.
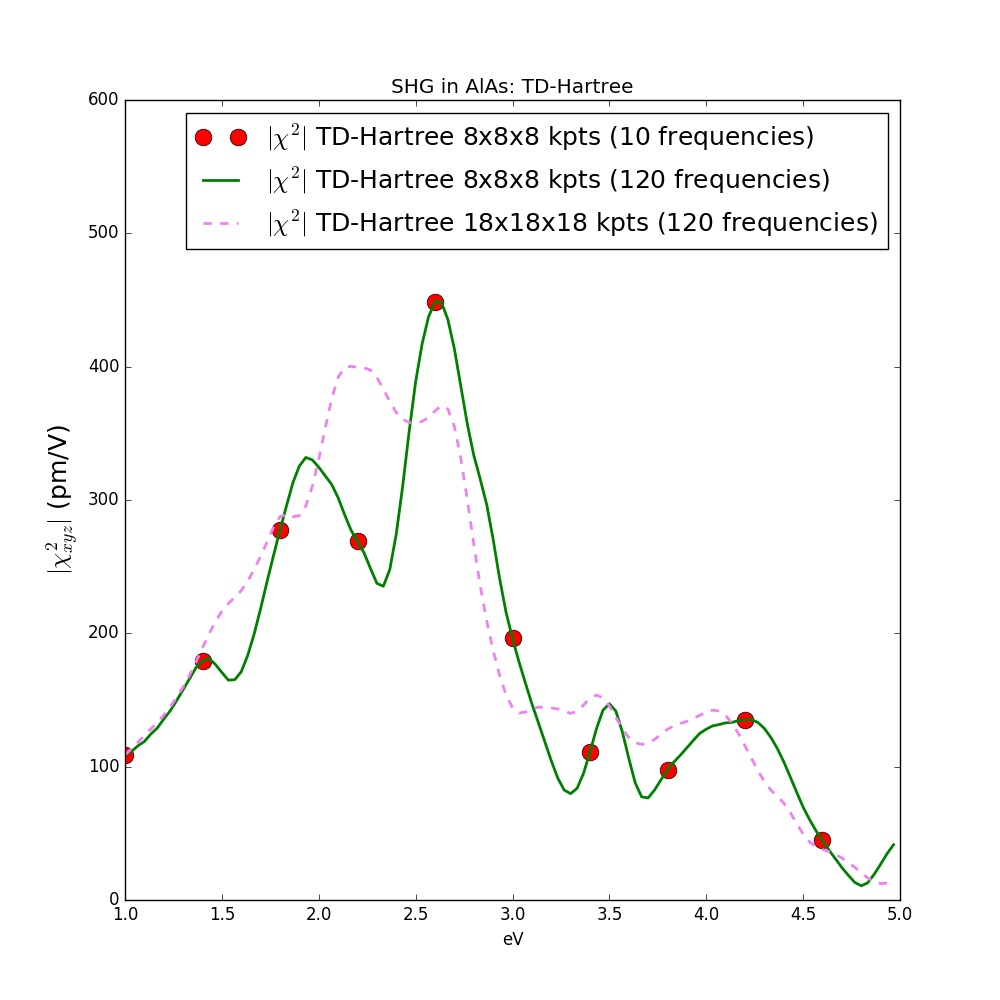
Time-dependent Hartree (RPA with local field effects)
In order to include local field effects in the SHG we use the Time-dependent Hartree approximation, see the theory page for more details. The input is generated with the usual command "lumen -u -V RL" where we turned on the Reciprocal Lattice vectors verbosity in order to specify the number of plane wave to use in the calculations. To run a TD-Hartree calculation you just specify NLCorrelation="HARTREE" and then we reduce the number of plane waves to 307, that is enough to have a converged result in this system.
nlinear # [R NL] Non-linear optics
% NLBands
3 | 6 | # [NL] Bands
%
NLintegrator="INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "HARTREE" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF")
NLLrcAlpha= 0.000000 # [NL] Long Range Correction
% NLEnRange
1.000000 | 5.000000 | eV # [NL] Energy range
%
NLEnSteps= 10 # [NL] Energy steps
HARRLvcs= 105 RL # [HA] Hartree RL components
EXXRLvcs= 105 RL # [XX] Exchange RL components
NLDamping= 0.250000 eV # [NL] Damping
% ExtF_Dir
1.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor
%
ExtF_kind= "SOFTSIN" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
In this run we increase the damping to 0.25 eV in such a way to speed up calculations. The result of this calculation is shown in the figure below:
Plot data are available here.
Time-dependent Density Functional Theory (TD-DFT)
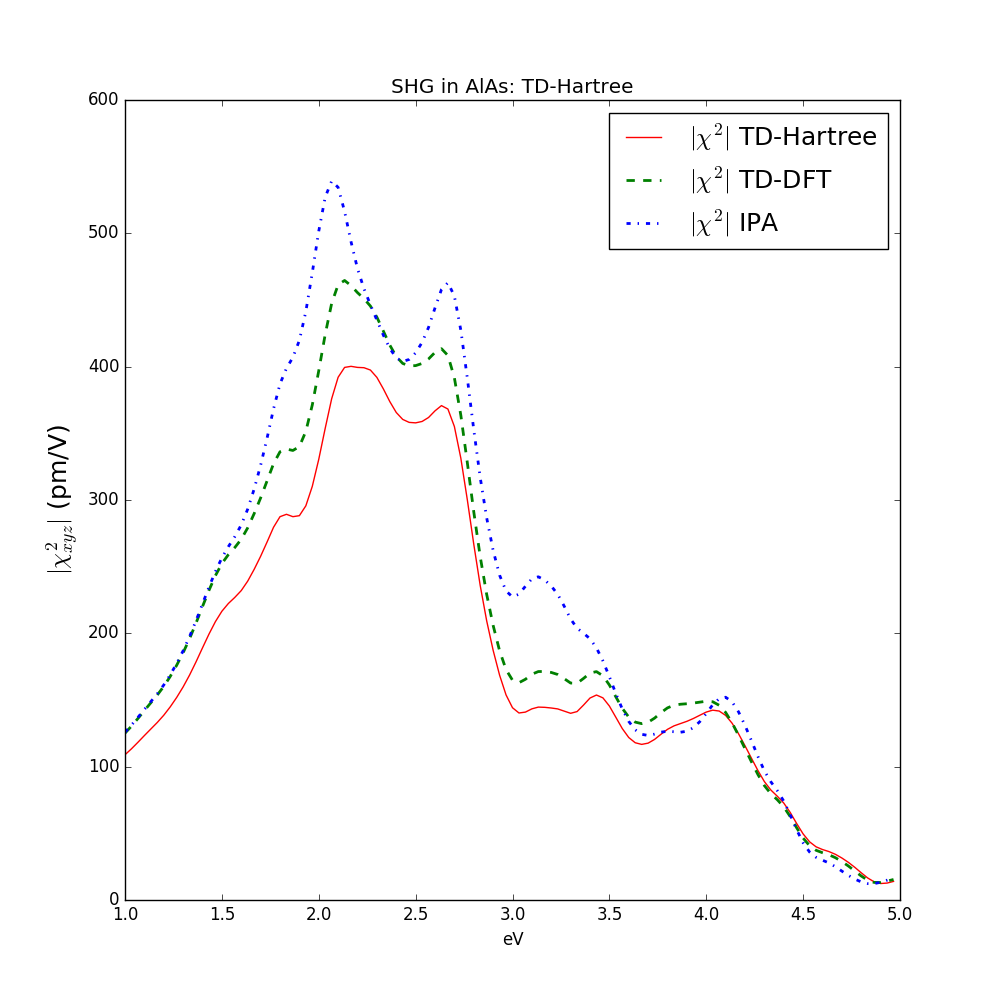
TD-DFT calculations are similar to the TD-Hartree ones. Just change NLCorrelation="TDDFT" and the exchange correlation functional used in the ground state calculations will be included in the real-time dynamics. Notice that only LDA or GGA functionals are supported by Yambo/Lumen. These functionals usually provide an insignificant improvement respect to the TD-Hartree because they miss the long-range part that will be included in the next tutorial by means of TD-DPFT theory. You can perform TD-DFT calculations as exercise and compare with the other approximations. The converged result on a 18x18x18 k-points grid is reported below:
Plot data are available here.
Time-dependent Density-Polarization Functional Theory (TD-DPFT)
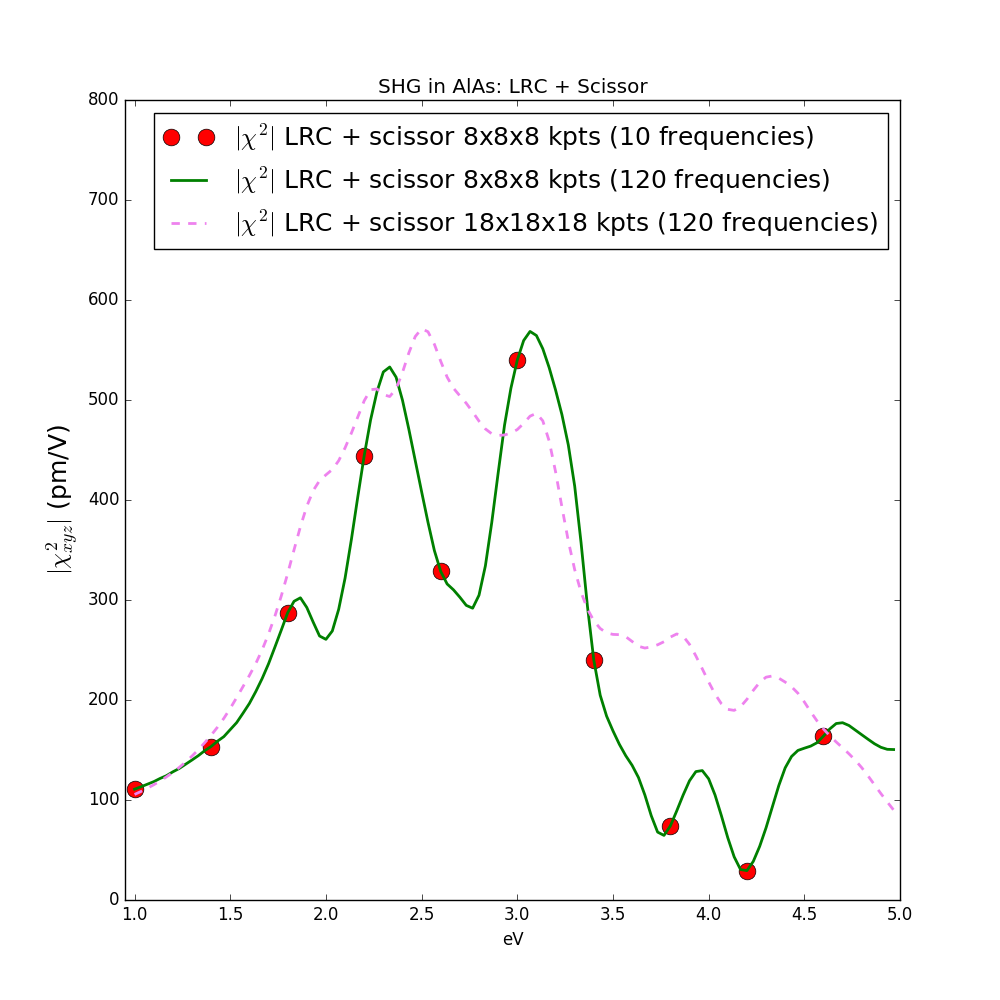
In this last tutorial on SHG we will include both quasi-particle effects by means of a scissor operator and long-range correction to the response function by means of Time-dependent Density-Polarization Functional Theory. The Lumen input can be generated as usual with the command lumen -u -V qp:
nlinear # [R NL] Non-linear optics
% NLBands
3 | 6 | # [NL] Bands
%
NLintegrator="INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "LRC" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM")
NLLrcAlpha= 0.350000 # [NL] Long Range Correction
% NLEnRange
0.200000 | 8.000000 | eV # [NL] Energy range
%
NLEnSteps= 10 # [NL] Energy steps
HARRLvcs= 105 RL # [HA] Hartree RL components
EXXRLvcs= 105 RL # [XX] Exchange RL components
NLDamping= 0.150000 eV # [NL] Damping
% ExtF_Dir
1.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor
%
ExtF_kind= "SOFTSIN" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
GfnQPdb= "none" # [EXTQP G] Database
GfnQP_N= 1 # [EXTQP G] Interpolation neighbours
% GfnQP_E
0.900000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim
%
The \( \alpha \) parameter for AlAs has been suggested by Botti and coworkers in PRB 69, 155112. The results is:
Plot data are available here. Notice that different models for the \( \alpha \) parameter have been proposed in the literature, see PRB 94 035149 (2016) for a discussion. Finally, in Yambo we implemented also the Jelium-with gap model NLCorrelation="JGM" that provides an automatic estimation of the \( \alpha \) parameters for each material, see M. Grüning, D. Sangalli, C. Attaccalite, Phys. Rev. B 94, 035149 (2016) for a discussion on this approximation.