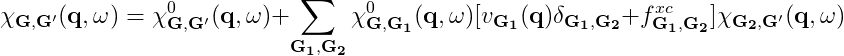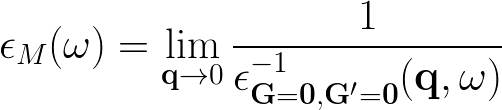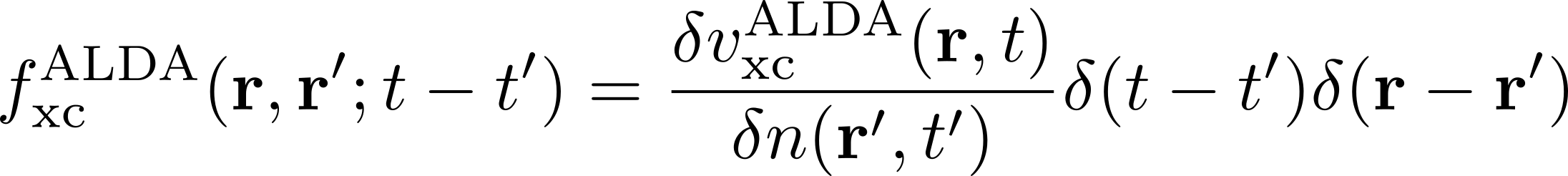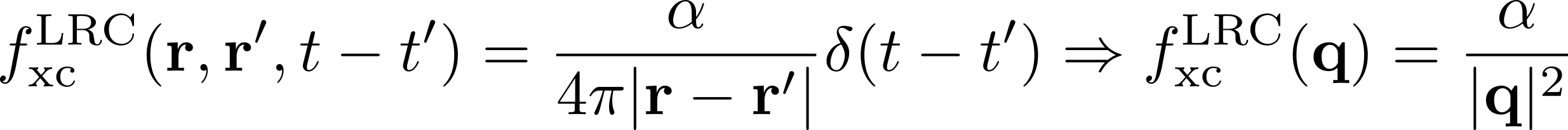Time-dependent density functional theory (standard kernel)

In this tutorial you will learn how to calculate optical spectra at the time-dependent density-functional theory level for bulk hBN.

Background

The macroscopic dielectric function is obtained by including the so-called local field effects (LFE) in the calculation of the response function. Within the time-dependent DFT formalism this is achieved by solving the Dyson equation for the susceptibility X. In reciprocal space this is given by:

The microscopic dielectric function is related to X by:

and the macroscopic dielectric function is obtained by taking the (0,0) component of the inverse microscopic one:

Experimental observables like the optical absorption and the electron energy loss can be obtained from the macroscopic dielectric function:

The f ^xc term is called the exchange-correlation (xc) kernel and describes the response of the xc potential at a time t to changes in the density at all previous times. Approximations for the xc kernel can be derived by taking the functional derivative of common approximations for the xc potential with respect to the density with the additional approximation that only instantaneous changes to the density are considered (adiabatic approximation).

Within this family we consider here the adiabatic local density approximation (ALDA)

As this module will show for bulk hBN this approximation provides spectra similar to the RPA when applied to extended systems (it has instead a significant impact on molecular excitations). One of the main problems that has been pinpointed in the literature is that ALDA and its likes miss a long range contribution essential to reproduce excitations in solids. Several approximations have been proposed to introduce this essential long range contribution.

Within this family we consider here the long-range correction approximation (LRC):

where α is an empirical parameter related to the system screening.

Note that approximations of this form cannot be rigorously justified within the sole time-dependent density-functional framework. Additional key quantities such as the electron density current or the macroscopic polarization need to be considered.

Prerequisites

• You must first complete the "How to use Yambo" and the "Optics at the independent particle level" and "local fields" modules

You will need:

• The SAVE databases for bulk hBN
• The yambo executable
• gnuplot, for plotting spectra

Choosing input parameters

Enter the folder for bulk hBN that contains the SAVE directory, and generate the input file. From yambo -H you should understand that the correct option is yambo -o c -k <opt> . Where <opt> can be 'hartree' as in the tutorial on the local fields, or 'alda' or 'lrc' respectively for the ALDA and LRC approximations for the xc kernel outlined above. Let's start by running the calculation with the ALDA kernel:

$ cd YAMBO_TUTORIALS/hBN-3D/YAMBO
$ yambo        (Initialization)
$ yambo -F yambo.in_ALDA -V RL -J 3D_ALDA -o c -k alda

We thus use a new input file yambo.in_ALDA, switch on the FFTGvecs variable, and label all outputs/databases with a 3D_ALDA tag. Make sure to set/modify all of the following variables to:

FFTGvecs=     30        Ry    # [FFT] Plane-waves
Chimod= "ALDA"            # [X] IP/Hartree/ALDA/LRC/BSfxc
FxcGRLc=     3        Ry    # [Xd] Response block size
NGsBlkXd=     3        Ry    # [Xd] Response block size
% QpntsRXd
 1 |  1 |                   # [Xd] Transferred momenta
%
% EnRngeXd
 0.00000 | 20.00000 | eV    # [Xd] Energy range
%
% DmRngeXd
0.200000 | 0.200000 | eV    # [Xd] Damping range
%
ETStpsXd= 2001               # [Xd] Total Energy steps
% LongDrXd
1.000000 | 1.000000 | 0.000000 |        # [Xd] [cc] Electric Field
%

In this input file, we have:

• A q parallel to the planes
• Selected the ALDA kernel, and expanded G-vectors in the screening and in the xc kernel up to 3 Ry (about 85 G-vectors)

Optics runlevel

For optical properties we are interested just in the long-wavelength limit q = 0. This always corresponds to the first q-point in the set of possible q=k-k' -points. Change the following variables in the input file to:

% QpntsRXd
 1 |  1 |                   # [Xd] Transferred momenta
%
ETStpsXd= 1001               # [Xd] Total Energy steps

in order to select just the first q. The last variable ensures we generate a smooth spectrum. Save the input file and launch the code, keeping the command line options as before (i.e., just remove the lower case options):

$ yambo -F yambo.in_IP -J Full
...
<---> [05] Optics
<---> [LA] SERIAL linear algebra
<---> [DIP] Checking dipoles header
<---> [x,Vnl] computed using 4 projectors
<---> [M  0.017 Gb] Alloc WF ( 0.016)
<---> [WF] Performing Wave-Functions I/O from ./SAVE
<01s> Dipoles: P and iR (T): |########################################| [100%] 01s(E) 01s(X)
<01s> [M  0.001 Gb] Free WF ( 0.016)
<01s> [DIP] Writing dipoles header
<01s> [X-CG] R(p) Tot o/o(of R)  :   5501   52992     100
<01s> Xo@q[1] |########################################| [100%] --(E) --(X)
<01s> [06] Game Over & Game summary
 
$ ls
Full   SAVE  yambo.in_IP   r_setup
o-Full.eel_q1_ip  o-Full.eps_q1_ip  r-Full_optics_chi

Let's take a moment to understand what Yambo has done inside the Optics runlevel:

1. Compute the [x,Vnl] term
2. Read the wavefunctions from disc [WF]
3. Compute the dipoles, i.e. matrix elements of p
4. Write the dipoles to disk as Full/ndb.dip* databases. This you can see in the report file:

$ grep -A20 "WR" r-Full_optics_chi 
[WR./Full//ndb.dip_iR_and_P]
Brillouin Zone Q/K grids (IBZ/BZ):  14   72   14   72
RL vectors                   (WF): 1491
Electronic Temperature        [K]: 0.0000000
Bosonic    Temperature        [K]: 0.0000000
X band range           :   1  100
RL vectors in the sum  : 1491
[r,Vnl] included       :yes
...

5. Finally, Yambo computes the non-interacting susceptibility X₀ for this q, and writes the dielectric function inside the o-Full.eps_q1_ip file for plotting

Energy cut off

Before plotting the output, let's change a few more variables. The previous calculation used all the G-vectors in expanding the wavefunctions, 1491. This corresponds roughly to the cut off energy of 40Ry we used in the DFT calculation. Generally, however, we can use a smaller value. We use the verbosity to switch on this variable, and a new -J flag to avoid reading the previous database:

$ yambo -F yambo.in_IP -J 6Ry -V RL -o c

Change the value of FFTGvecs and also its unit from RL (number of G-vectors) to Ry (energy in Rydberg):

FFTGvecs= 6           Ry    # [FFT] Plane-waves

Save the input file and launch the code again:

 $ yambo -F yambo.in_IP -J 6Ry -V RL

and then plot the o-Full.eps_q1_ip and o-6Ry.eps_q1_ip files:

$ gnuplot
gnuplot> plot "o-Full.eps_q1_ip" w l,"o-6Ry.eps_q1_ip" w p

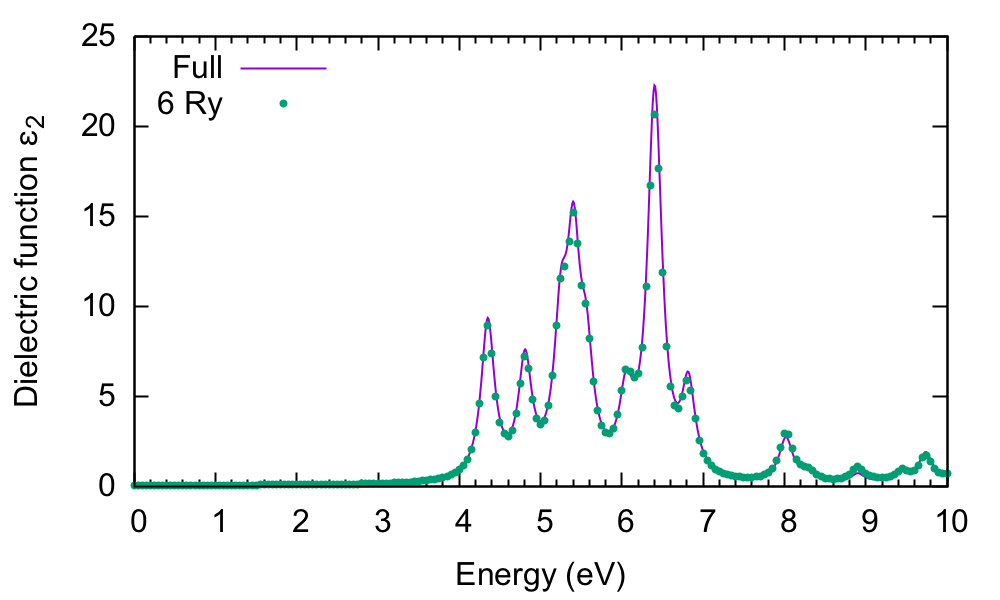
Clearly there is very little difference between the two spectra. This highlights an important point in calculating excited state properties: generally, fewer G-vectors are needed than what are needed in DFT calculations. Regarding the spectrum itself, the first peak occurs at about 4.4eV. This is consistent with the minimum direct gap reported by Yambo: 4.28eV. The comparison with experiment (not shown) is very poor however.

If you make some mistake, and cannot reproduce this figure, you should check the value of FFTGvecs in the input file, delete the 6Ry folder, and try again - taking care to plot the right file! (e.g. o-6Ry.eps_q1_ip_01).

q-direction

Now let's select a different component of the dielectric tensor:

$ yambo -F yambo.in_IP -J 6Ry -V RL -o c
...
% LongDrXd
0.000000 | 0.000000 | 1.000000 |        # [Xd] [cc] Electric Field
%
...
$ yambo -F yambo.in_IP -J 6Ry -V RL

This time yambo reads from the 6Ry folder, so it does not need to compute the dipole matrix elements again, and the calculation is fast. Plotting gives:

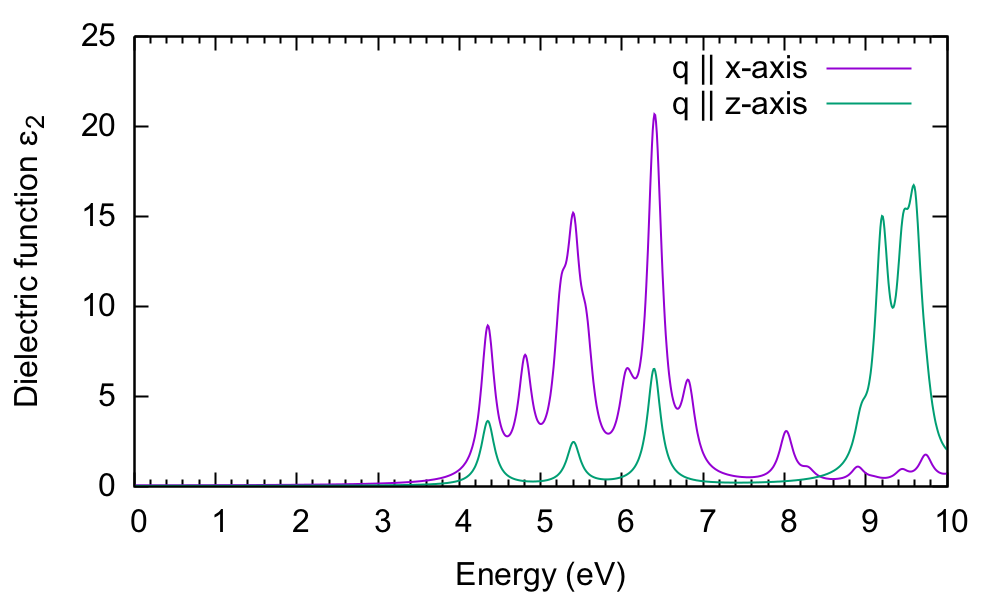
$ gnuplot
gnuplot> plot "o-6Ry.eps_q1_ip" t "q || x-axis" w l,"o-6Ry.eps_q1_ip_01" t "q || c-axis" w l

The absorption is suppressed in the stacking direction. As the interplanar spacing is increased, we would eventually arrive at the absorption of the BN sheet (see Local fields tutorial).

Non-local commutator

Last, we show the effect of switching off the non-local commutator term (see [Vnl,r] in the equation at the top of the page) due to the pseudopotential. As there is no option to do this inside yambo, you need to hide the database file. Change back to the q || (1 0 0) direction, and launch yambo with a different -J option:

$ mv SAVE/ns.kb_pp_pwscf SAVE/ns.kb_pp_pwscf_OFF
$ yambo -F yambo.in_IP -J 6Ry_NoVnl -o c
$ yambo -F yambo.in_IP -J 6Ry_NoVnl

Note the warning in the output:

<---> [WARNING] Missing non-local pseudopotential contribution

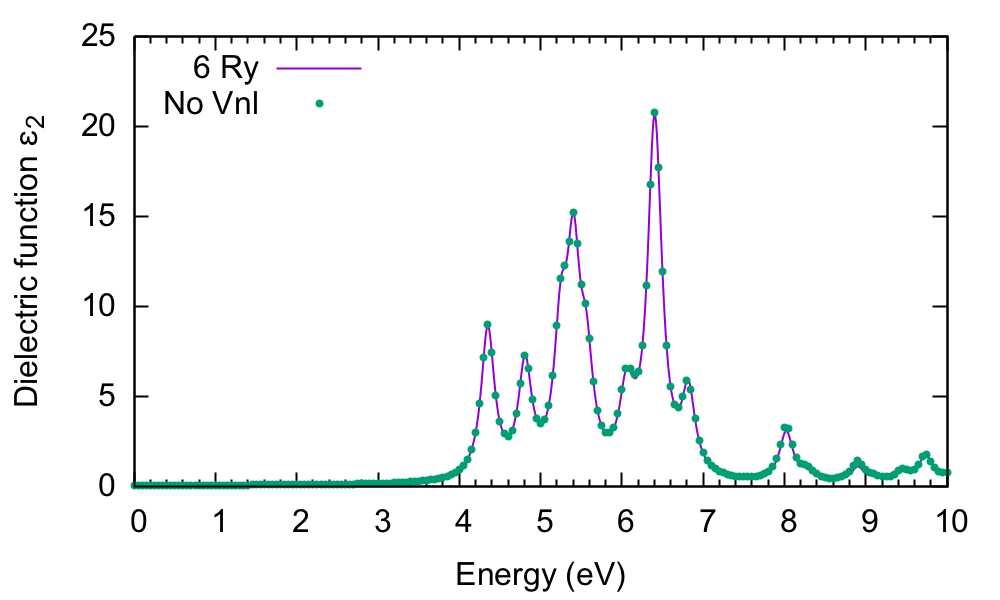
which also appears in the report file, and noted in the database as [r,Vnl] included :no. The difference is tiny:

However, when your system is larger, with more projectors in the pseudopotential or more k-points (see the BSE tutorial), the inclusion of Vnl can make a huge difference in the computational load, so it's always worth checking to see if the terms are important in your system.

Summary

From this tutorial you've learned:

• How to compute a simple optical spectrum
• How to reduce the computational load through reducing the G-vector/energy cut off and removing the Vnl term
• How to plot different components of the dielectric tensor
• How to use the -J option to neatly label and organise files and databases

Links

• Next module: Local fields
• Back to First steps with yambo tutorial
• Back to tutorials menu