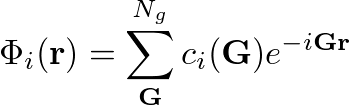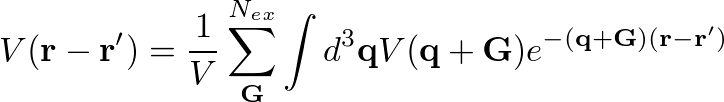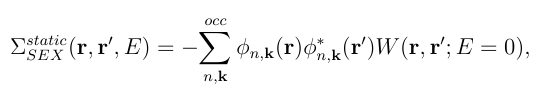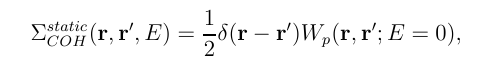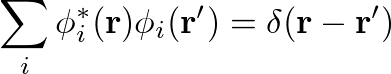Hartree Fock and GW

Basic concepts of the GW approximation by the Yambo Team

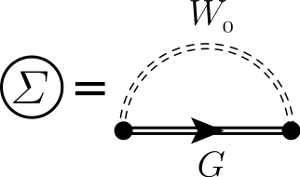
In this tutorial you will learn the basic concepts of the Hartree-Fock and of the GW[[[6]]] approximations. In particular we will illustrate how to calculate Quasi-Particle energies with a single shot G₀W₀ approximation. Different lecture notes on the GW approach are available in the "Lecture Notes" section.

The tutorial is split in different sections. In the first part we will deal with Hartree-Fock (HF) and the Coulomb-hole and screened-exchange (COHSEX) approximation. Finally in the last section we will discuss dynamical correlation with a Plasmon Pole Approximation (PPA).

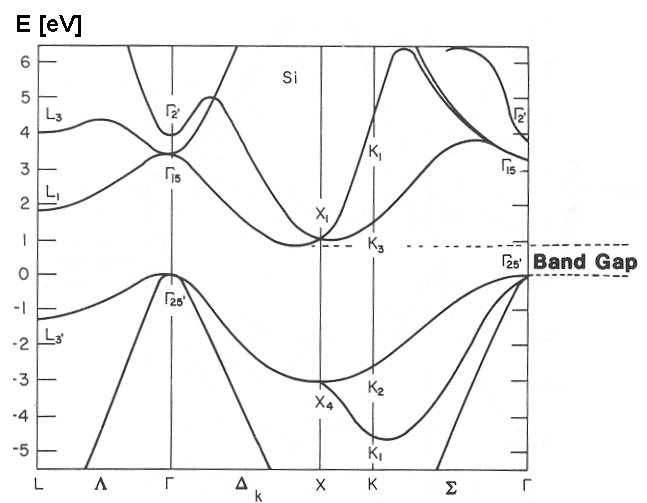
The material: Silicon

Bulk Silicon FCC lattice Two atoms per cell (8 electrons) Lattice constant 10.183 [a.u.] Plane waves cutoff 15 Rydberg

The Tutorial structure

Once the tutorial zip file is unzipped the following folder structure will appear

COPYING README Solid_Si/
with the Solid_Si folder containing
>ls Solid_Si/ Pwscf/ YAMBO/

• In the Pwscf folder information on the ground state generation are provided. In particular the student will find an input/output directory with input/output files for pw.x. Also a psp folder is provided with the silicon pseudo files.
• The YAMBO folder contains the Yambo input/output files and core databases.

Hartree-Fock

Now we will study the convergence of the Hartree-Fock self energy, respect to the number of G-vectors and k-points. Yambo is a plane-wave code, therefore all the operators and wave-functions are expanded as:

--- Test SimpleMathJax: [math]\displaystyle{ \Phi_i({\bf r1}) = \sum_{\bf G}^{N_G} c_i({\bf G}) e^{i{\bf G}\cdot{\bf r}} }[/math] ---

Before you start any calculations we can decide how many G-vectors you want use to represent your wave-function. By default Yambo will use all of them, and for the present tutorial this is fine, however if you are studying larger systems you would like to reduce them in order to speed-up calculations, you can do it with yambo -i -V RL and then changing the variable MaxGvecs that referees to N_g in the previous formula.

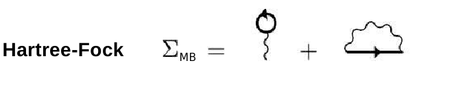
Now we will proceed in the calculation of the Hartree-Fock(HF) exchange. This is composed of two terms, that Hartree and the Fock (or exchange) one:

In this tutorial we will calculate only the first order correction to the Kohn-Sham Hamiltonian due to the exchange term. Because of we are working in periodic system, the most appropriate basis to represent the Coulomb potential, appearing in the Fock term, is a plane-wave basis:

In order to generate the input file for the exchange type yambo -x. The variable that governs the number of G vectors N_ex in the Coulomb potential is EXXRLvcs. In addition notice that in the previous formula for V(r-r') we have an integral on the q vector, that in the code is discretized on a regular q-grid generated from the k-point one, q=k-k'.

K-points convergence

Enter the YAMBO folder

>cd YAMBO/ >ls Convergence_Plots 2x2x2 4x4x4 6x6x6 8x8x8 Gamma
Enter each grid folder and run >yambo without options. Then type

yambo -x -F INPUTS/01HF_corrections

and edit the 01HF_corrections file

HF_and_locXC                 # [R XX] Hartree-Fock Self-energy and Vxc
EXXRLvcs= 7           Ry    # [XX] Exchange RL components
%QPkrange                    # [GW] QP generalized Kpoint/Band indices
  1|  8|  1| 15|
%
%QPerange                    # [GW] QP generalized Kpoint/Energy indices
  1|  8| 0.0|-1.0|
%
 

setting EXXRLvcs=7 Ry . Then run in each k-point folder

yambo -F INPUTS/01HF_corrections -J HF_7Ry

Note that after the each run Yambo produces three output file, one starting with r_... , another with l_... and a third one starting with o_.... The first one is a report of the actual calculation with all the details of the system, input, and results, while the second is a log with the running time of each process.

The file we are most interested in is the output file, o-HF_7Ry.hf. This file contains several columns. The fourth, labelled with Ehf represents the Hartree-Fock energy. This is the quantitu we have to look at.

G-vectors convergence

Enter the 4x4x4 folder and edit the 01HF_corrections file changing the field EXXRLvcs=3,6,7 and 15 Ry. For each case run

yambo -F INPUTS/01HF_corrections -J HF_???Ry

with ???=3,6,7 and 15

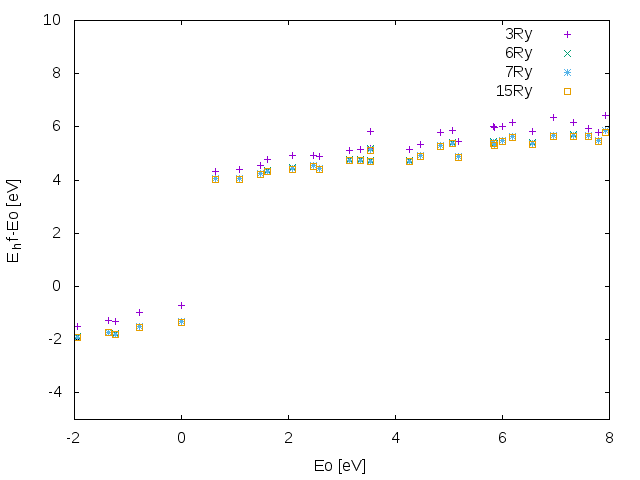
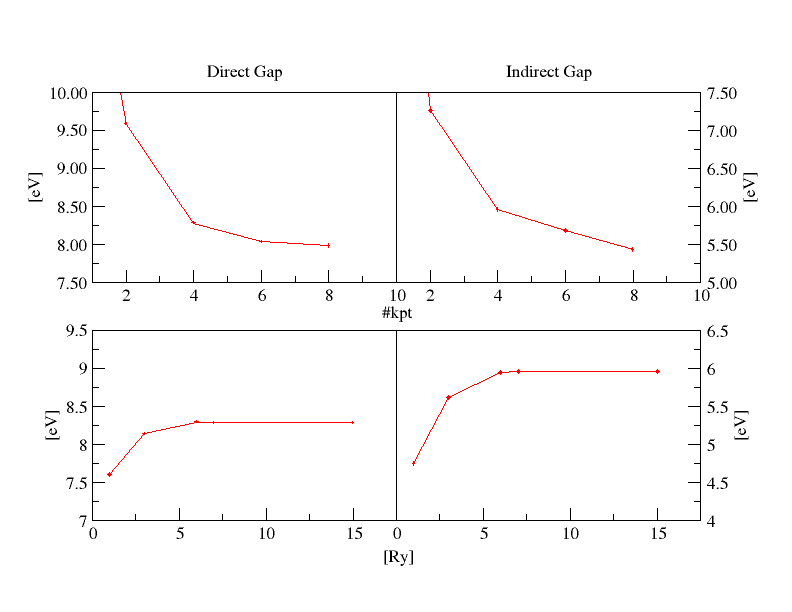
The results of this series of calculations are summarized in the following plots. Note the rapid convergence with the number of k-points.

To obtain the plots of the following graphs just plot the columns #4-#3 versus #3 of the o.hf files.

COHSEX without empty bands

The Hartree-Fock self-energy just described in the previous section, although successful on some molecular systems, miserably fails in extended systems. The reason of this failure lies in the fact that electrons can screen the Coulomb potential, and therefore one electron feels a screened potential instead of the bare one. A common approximation for this screened potential is the so-called Random Phase Approximation:

where the bare Coulomb potential V(r) is replaced by a non-local and frequency dependent one W(r,r',ω). Subsequently it is possible to redefine all the perturbation theory in term of this screened potential, and disregarding the additional corrections coming from the vertex part, one obtains the so-called GW approximation.

However the substantial complexity associated with calculating the non-local, energy dependent Σ=GW operator inspired early efforts to find simplifying approximations as the static COHSEX approximation prosed by Hedin[[[4]]]. The Coulomb Hole plus Screened Exchange (COHSEX) approximation[[[2]],3] eliminates the summation over empty states for the self energy operator and has the added benefit of being a static operator, a particular simplification for self consistent calculations. With the COHSEX approximation the self-energy is composed of two parts:

where W_p=W - V.
In order to calculate the COHSEX self-energy with yambo you need first the static screened interaction yambo -b -k hartree. As for the V(r) case, also W(r,r',E=0) will depend from the number of G-vectors, and the k-grid, but this time also the number of conduction bands XsBndsRn will enter in the screening calculation through the polarization function, see The Interacting response function: Many-Body and TDDFT section. Notice however that there are not any additional dependence of the self-energy operator from the conduction bands. After you obtained the screened interaction you are ready to build the self-energy operator and solve the corresponding Dyson equation, have a look to the Dyson Equation solvers in Yambo. In order to get the quasi-particle energies, just do yambo -b -g n -k hartree. After calculation are completed Yambo will produce an output file o.qp which contains the values of the bare and re-normalized energy levels.

K-points convergence

Follow the same strategy of the HF case. Enter each k-point folder and type

> yambo -b -k hartree -g n -p c -F INPUTS/02Cohsex edit the input file and change the values of the fields

EXXRLvcs=7 Ry %BndsRnXs

 1 | 10  |                   # [Xs] Polarization function bands

% NGsBlkXs= 1 RL # [Xs] Response block size

1. UseEbands # [GW] Force COHSEX to use empty bands

%QPkrange # [GW] QP generalized Kpoint/Band indices

1|  8|  1| 10|

% leaving the other parameters unchanged. Now, in each k-point folder, run

>yambo -F INPUTS/02Cohsex -J Cohsex_HF7Ry_X0Ry-nb10

W size convergence

Enter the 4x4x4 folder and edit the 02Cohsex_corrections file changing the field NGsBlkXs=3,6,7 Ry. Run

>yambo -F INPUTS/02Cohsex -J Cohsex_HF7Ry_X???Ry-nb10 with ???=3,6,7 and 15

W bands

Open your input file and change only the input variable NGsBlkXs=1 Ry. Then change %BndsRnXs 1 | 20 | # [Xs] Polarization function bands %

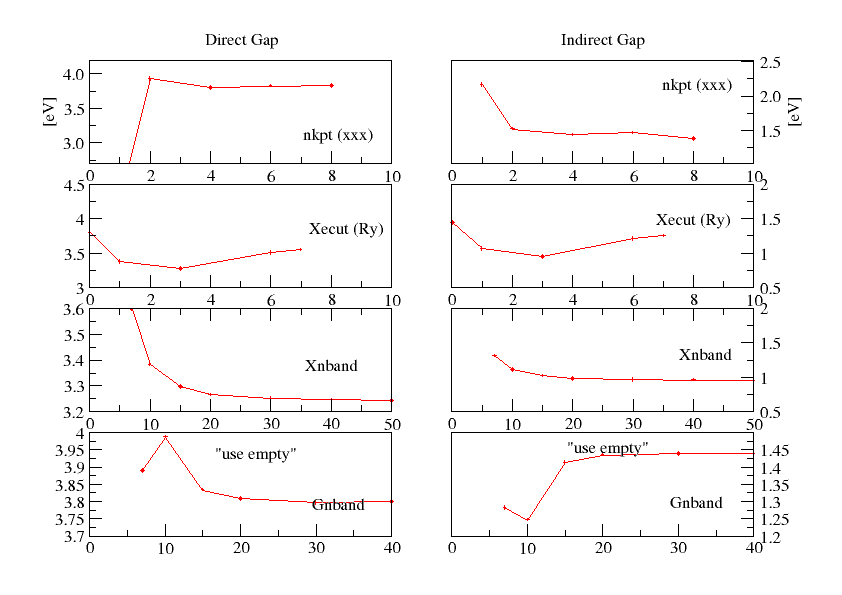
and run yambo -F INPUTS/02Cohsex -J Cohsex_HF7Ry_X1Ry-nb20. Repeat the calculations using 30 and 40 bands changing nb??? in the job string identifier. Finally check how the Chosex Direct and Indirect band gap behave as a function of the number of bands in the screening.

COHSEX with empty bands

While the Screened Exchange(SEX) part of the COHSEX self-energy has a structure similar to the Hartree-Fock exchange term, the Coulomb Hole(COH) acts as static external potential on the electrons. In the COH part the delta function δ(r-r') comes from the completeness relation:

Now we avoid the use of this relation in such a way to have a self-energy that depends from the conduction bands too. This can be done uncommenting flags UseEbands and setting the number of bands in the Green's function: % GbndRnge 1 | 10 | # [GW] G[W] bands range % Repeat the previous calculations with different GbndRnge for instance, 10 20 30 40, and check how the COHSEX direct and indirect band gap behave as a function of the number of bands in the Green's function.
Recently an enhanced version of the COHSEX approximation has been proposed, if you want learn more have a look to the reference[[[4]]].

The plasmon pole approximation

Even the static COHSEX approximation is very appealing, it was clear from the first calculation that dynamical effects cannot be disregarded in solids[[[6]]]. This fact motivated the research for approximated way to deal with a frequency dependent interaction, and one of the first proposal was the so-called Plasmon-Pole Approximation (PPA) (see ref. [[[7]]]).

Now we will proceed to the calculation of the silicon band gap in G₀W₀ within PPA. In each section you will be asked to perform several calculations varying the value of the relevant variables involved. More specifically let's consider a typical Yambo input file to calculate GW corrections in the PPA.

gw0 # [R GW] GoWo Quasiparticle energy levels ppa # [R Xp] Plasmon Pole Approximation HF_and_locXC # [R XX] Hartree-Fock Self-energy and Vxc em1d # [R Xd] Dynamical Inverse Dielectric Matrix EXXRLvcs= 7 Ry # [XX] Exchange RL components % QpntsRXp

 1 |  8 |                   # [Xp] Transferred momenta

% % BndsRnXp

  1 | 30 |                 # [Xp] Polarization function bands

% NGsBlkXp= 7 Ry # [Xp] Response block size % LongDrXp

1.000000 | 0.000000 | 0.000000 |        # [Xp] [cc] Electric Field

% PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy % GbndRnge

  1 |  30 |                 # [GW] G[W] bands range

% GDamping= 0.10000 eV # [GW] G[W] damping dScStep= 0.10000 eV # [GW] Energy step to evalute Z factors DysSolver= "n" # [GW] Dyson Equation solver (`n`,`s`,`g`) %QPkrange # [GW] QP generalized Kpoint/Band indices

 1|  8|  1| 10|

% %QPerange # [GW] QP generalized Kpoint/Energy indices

 1|  8| 0.0|-1.0|

% The variables are the same of the COHSEX case plus a new one PPAPntXp that describes the imaginary energy used to fit the Plasmon Pole model.
Follow the same strategy of the COHSEX case. Enter each k-point folder and type:

 
yambo -d -k hartree -g n -p p -F INPUTS/03GoWo_PPA_corrections

otherwise you can use the existent file Input/03GoWo_PPA_corrections. Now you have to study the convergence of the G₀W₀ gap versus the number of k-points, the number of bands in χ BndsRnXs, the size of the dielectric constant NGsBlkXs and the number of bands in the Green's function GbndRnge.

Please follow the same strategy of the COHSEX case running yambo using

yambo -F INPUTS/03GoWo_PPA_corrections -J GoWo_PPA_HF7Ry_X???Ry-nb???_nb??? The final convergence plots should look like these.

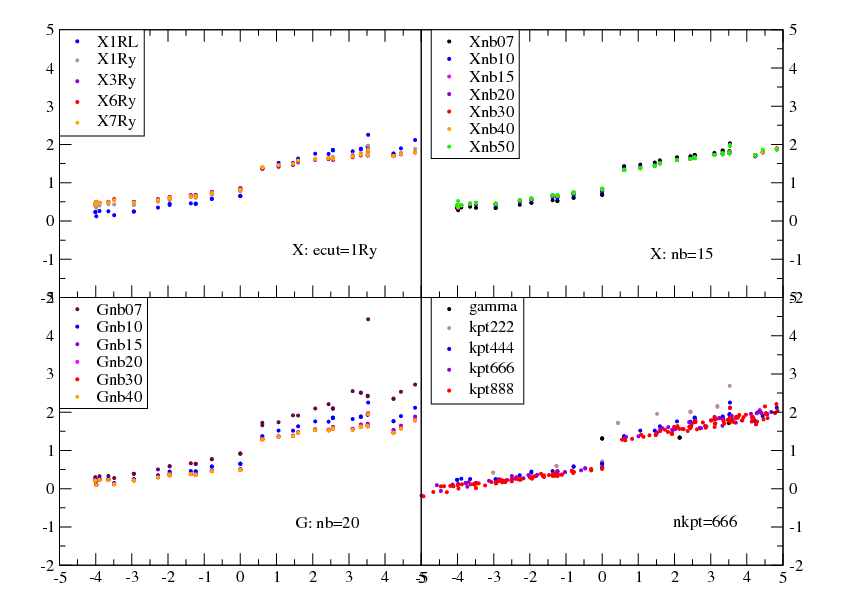
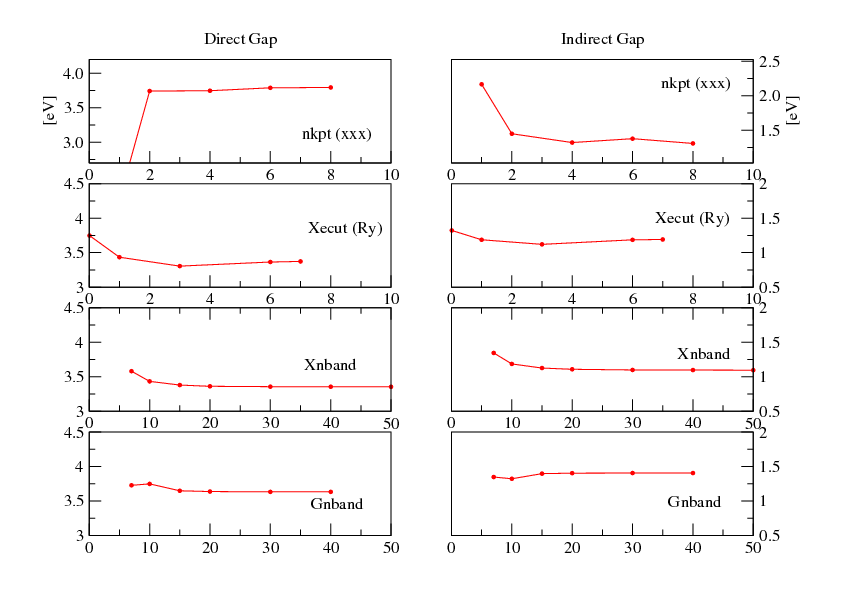
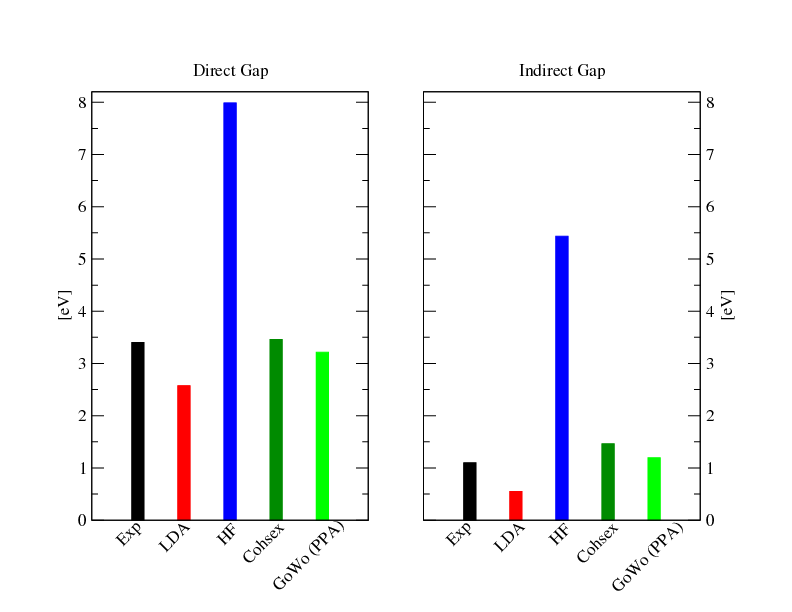
Final runs!! Now you know how to converge a G₀W₀ calculation so you can decide which are the parameters needed for full convergence. First do a COHSEX and then a GoWo (PPA) run at convergence, and you should obtain results similar to the following graph:

Curiosity: What's happen if the PPA fails? Have a look to the tutorial on the Real-Axis Integration.

References

1. Silicon on wikipedia.
2. Electron Correlation in the Solid State, Norman H. March (1999).
3. GW approach to the calculation of electron self-energies in semiconductors, B. Farid et al., Phys. Rev. B 38, 7530 (1988).
4. New Method for Calculating the One-Particle Green's Function with Application to the Electron-Gas Problem L. Hedin, Phys. Rev. 139, A796 (1965).
5. Enhanced Static Approximation to the Electron Self-Energy Operator for Efficient Calculation of Quasiparticle Energies, Wei Kang, Mark S. Hybertsen, Phys. Rev. B 82, 195108 (2010).
6. Dynamical Correlation Effects on the Quasiparticle Bloch States of a Covalent Crystal, G. Strinati, H. J. Mattausch, and W. Hanke , Phys. Rev. Lett. 45, 290 (1980).
7. Space-time method for ab initio calculations of self-energies and dielectric response functions of solids, H. N. Rojas, R. W. Godby, and R. J. Needs, Phys. Rev. Lett. 74, 1827 (1995) .