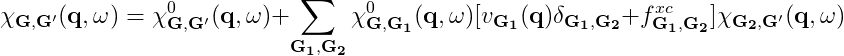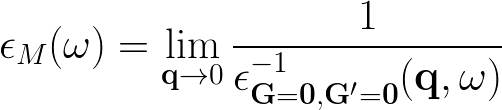Local fields

In this tutorial you will learn how to calculate the macroscopic dielectric function for bulk hBN (i.e. including local field effects- LFE) by solving the Dyson equation for X:

The microscopic dielectric function is related to X by:

and the macroscopic dielectric function is obtained by taking the (0,0) component of the inverse microscopic one:

Here we will use the RPA level: thus f ^xc=0 in the above (Hartree kernel).

Prerequisites

• You must first complete the "How to use Yambo" tutorial

You will need:

• The SAVE databases for 2D hBN
• The yambo executable
• gnuplot, for plotting spectra

Choosing input parameters

Enter the folder for 2D hBN that contains the SAVE directory, and generate the input file. From yambo -H you should understand that the correct option is yambo -o c -k hartree. Let's start by running the calculation for light polarization q in the plane of the BN sheet:

$ cd YAMBO_TUTORIALS/hBN-2D/YAMBO
$ yambo -F yambo.in_RPA -V RL -J q100 -o c -k hartree

and make sure to set/modify all of the following variables to:

FFTGvecs=     6        Ry    # [FFT] Plane-waves
Chimod= "Hartree"            # [X] IP/Hartree/ALDA/LRC/BSfxc
NGsBlkXd= 3            Ry    # [Xd] Response block size
% QpntsRXd
 1 |  1 |                   # [Xd] Transferred momenta
%
% EnRngeXd
 0.00000 | 20.00000 | eV    # [Xd] Energy range
%
% DmRngeXd
0.200000 | 0.200000 | eV    # [Xd] Damping range
%
ETStpsXd= 2001               # [Xd] Total Energy steps
% LongDrXd
1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
%

In this input file, we have the following:

• A q perpendicular to the sheet
• A wider energy range than before, and more broadening
• Selected the Hartree kernel, and expanding G-vectors up to 3 Ry (about 85 G-vectors)

Run the code

$ yambo -F yambo.in_RPA -V RL -J q100 

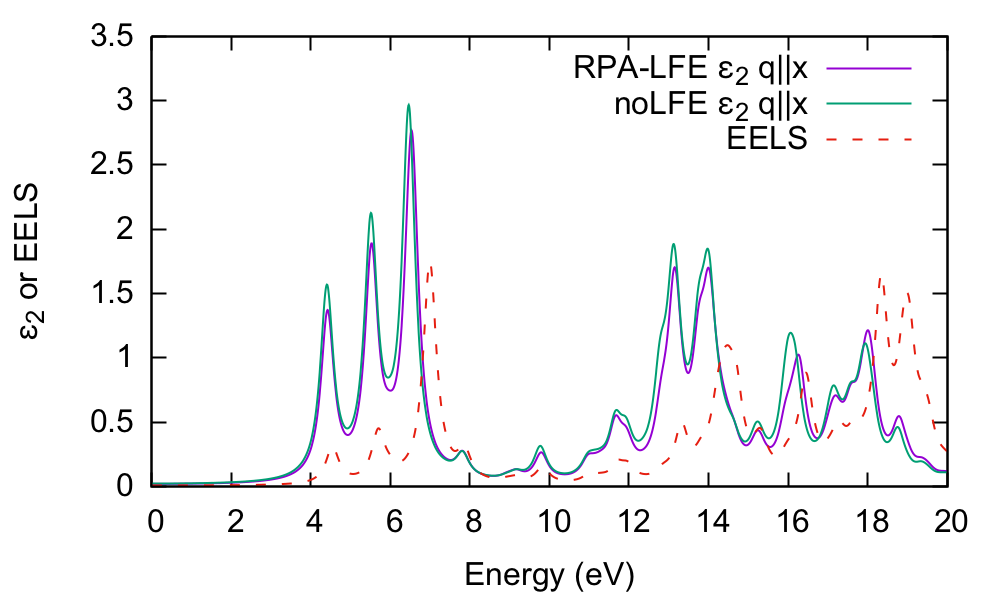
and let's compare the absorption with and without the local fields included. By inspecting the 'o-q100.eps_q1_inv_rpa_dyson' file it's clear we need the 2nd and 4th columns, respectively:

#  E/ev[1]     EPS-Im[2]   EPS-Re[3]   EPSo-Im[4]  EPSo-Re[5]

Plotting the result:

$ gnuplot
gnuplot > plot "o-q100.eps_q1_inv_rpa_dyson" u 1:2 t "q||x RPA-LFE" w l,"o-q100.eps_q1_inv_rpa_dyson" u 1:4 t "q||x noLFE" w l

It is clear that there is little influence of local fields in this case. We have also plotted the EELS spectrum for comparison.

Now let's switch to q perpendicular to the BN plane:

$ yambo -F yambo.in_RPA -V RL -J q001 -o c -k hartree        and set
...
% LongDrXd
0.000000 | 0.000000 | 1.000000 |        # [Xd] [cc] Electric Field
%
...
$ yambo -F yambo.in_RPA -V RL -J q001

Plotting the output file:

$ gnuplot
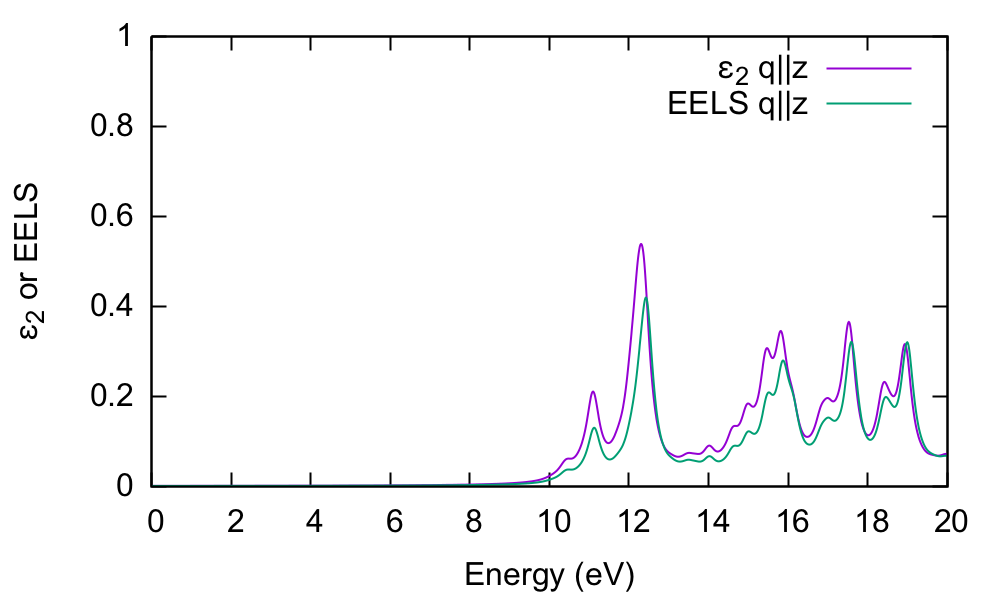
gnuplot> plot "o-q001.eps_q1_inv_rpa_dyson" u 1:2 t "RPA-LFE {/Symbol e}_2 q||z" w l,"o-q001.eps_q1_inv_rpa_dyson" u 1:4 t "noLFE {/Symbol e}_2 q||z" w l

In this case, the absorption is strongly blueshifted. Furthermore, the influence of local fields is striking, and quenches the spectrum strongly.

In order to understand this, we plot the electron energy loss spectrum for this component and compare with the absorption:

$ gnuplot
gnuplot > plot "o-q001.eps_q1_inv_rpa_dyson" u 1:2 t "q||z {/Symbol e}_2" w l,"o-q001.eel_q1_inv_rpa_dyson" u 1:2 t "q||z EELS" w l

The conclusion is that the dielectric function and EELS coincide for isolated systems, while this is not the case for periodic systems.

Summary

From this tutorial you've learned:

• How to compute a simple optical spectrum
• How to reduce the computational load through reducing the G-vector/energy cut off and removing the Vnl term
• How to plot different components of the dielectric tensor
• How to use the -J option to neatly label and organise files and databases

Links

• Local fields
• Back to tutorials menu