The magneto-optical Kerr effect

By default yambo computes the absorption of linearly polarized light. With specific keywords in the input file, however, yambo is also able to compute the absorption of circularly polarized light, through the computation of the off-diagonal components of the dielectric tensor. In this tutorial we will learn how to take advantage of it for the description of the magneto-optical Kerr effect (MOKE) in the polar geometry.

Prerequisites

Databases

For this tutorials we provide two yambo databases (DBs) for bulk iron. The first DB is the results of a Spin-DFT calculation while the second of a spinorial DFT calculation with the SO effect included both in the Hamiltonian and in the pseudo-potential. Both DBs are generated with the HGH pseudo-potentials.

• Ground State files (optional): Iron_abinit_gs_files.tar.gz
• Input and Reference files: Iron_Inputs.tar.gz
• Yambo core databases (48 Mb): Iron_DBs.tar.gz

Alternatively you can re-generate the DBs by your-self (also because the DB provided have been generated with small convergence parameters). To this end you just need to download and compile abinit, and generate the DBs using the input files and the pseudo-potentials provided. If you prefer, you can also try to generate the same DBs with the PWscf package (however you need to find a proper pseudo-potential).

Input files

We also provide the input files for yambo (and ypp). If you prefer to generate the input files by yourself you will just need to use the command

 yambo -i -F Input/01_init

for the initialization and

 yambo -opsics bse -V resp -F Input/"0n_filename"

Among the varaibles activated with the -V resp option we will use these options which are specific for metals:

 Gauge= "length"              # [BSE] Gauge (length|velocity). In metals length misses An-Hall
 DrudeWBS=  (4.80, 5.65)  eV  # [BSE] Drude plasmon

For the computation of the kerr parameters yambo_kerr will just need two special input varaibles

 BSEprop="abs kerr"           # [BSE] Can be any among
 AnHall                       # [BSE] Compute the anomalous Hall effect and if length add it to eps

which are activated by default using the yambo executable. Other variables not used in the present tutorial have been erased to simplify the input files.

Few equations

The MOKE consist in a different absorpion of the right (+) and left (-) circularly polarized light expirienced in magnetic materials. The dielectric function ε±(ω) can be constructed from the dielectric tensor:

Here "z" is the direction of the magnetization and of the propagation of the light, while the polarization lays in the "xy"-plane. The absorption is often expressed in terms of the optical conductivity which is related to the dielectric tensor trough the equation

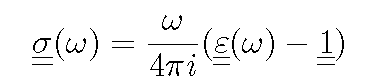
This effect is due to the coupling of the magnetization with the spatial part of the wave-function trough the SO interaction. The result is that linearly polarized light is rotated and deformed upon reflection from a magnetic material. The rotation and deformation constitute the Kerr parameters, which are frequency dependent and can be expressed, in the small angles limit with a simple equation

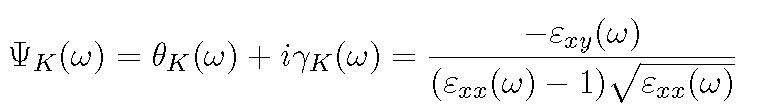
We also suggest to have a look to these references for a detailed discussion of the different components of the dielectric tensor, as well as for a discussion about the length and the velocity gauges , , , . In this tutorial you will compute the kerr effect only at the independent particle version. However in the released version of the code it is also possible to compute the Kerr effect at the BSE level .

Length and velocity gauge

The length and velocity gauge dielectric function are defined via

[math]\displaystyle{ \epsilon(\omega)=1-4\pi/q^2 \chi_{\rho\rho}(\omega) }[/math]

and

[math]\displaystyle{ \epsilon(\omega)=1-4\pi/\omega^2 \chi_{jj}(\omega) }[/math]

The two should in principle give identical results. However, in the earlier implementations, the same complex [math]\displaystyle{ \omega+i\eta }[/math] expression was used both in the response function and in the pre-factor appearing in the velocity gauge, leading to small differences in the final results. This has been fixed in more recent versions of the code

Optical Properties of Bulk Iron

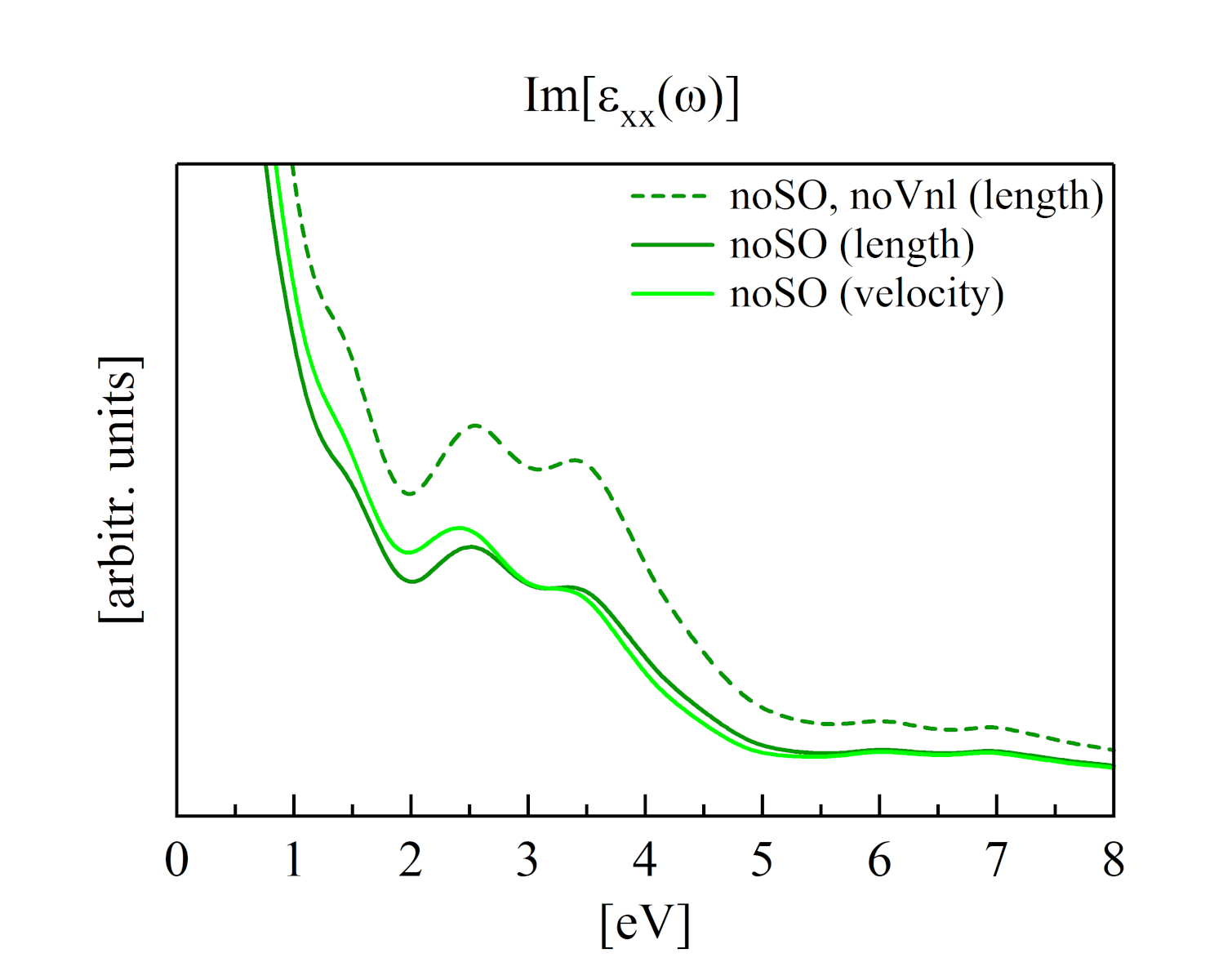
Bulk iron is a common transition metal which displays a spin-polarized ground state. In this system the magnetic moments of the spin-polarized ions couple to give a ferromagnetic ground state. It is a metal with a simple FCC structure. As a consequence the local-fields effect (i.e. the G≠0 terms of the e-h exchange interaction) is almost negligible in the description of the absorption properties of the system. Moreover the delocalized electrons completly screen the direct e-h interaction and thus the so called independent-particle random-phase-approximation (IP-RPA) is sufficient to describe the absorption properties. Recall that in this not a bare IP approximation, because the macroscopic term of the exchange interaction (i.e. the G=0 term) is taken into account (RPA). On the contrary it is known that for d electrons the commutator of [x,Vnl] give non-negligible corrections to the spectrum. Thus as a first step we will check this effect in the case of HGH pseudo-potential.

First, go in the withoutSO directory

 cd withoutSO 

run the initialization

 yambo -F Inputs/01_init 

and then compute the absorption spectrum. To this end, have a look to the input file 02_IP-RPA_len , to understand the parameters. In particular check the input variable DrudeWBS. The presence of this variable means that the intra-band contibution to the absorption is described phenomenlogically, with a semi-classical model. Now run

 yambo -F Inputs/02_IP-RPA_len -J 02_IP-RPA_len ;

yambo will compute the absorption in the length gauge (this is the standard gauge used by yambo) including the term [x,Vnl] by default. To check the importance of this term first hide the ns.kb_pp DB,

 mv SAVE/ns.kb_pp SAVE/hide_ns.kb_pp

and then run the code again

 yambo -F Inputs/02_IP-RPA_len -J 02_IP-RPA_len_noVnl .

[Hint: the most time consuming part of this calulation is the computation of the dipoles. You can avoid yambo_kerr to re-compute each time the dipoles preparing the database in the correct directory. In this case just do, before running yambo:

 mkdir 02_IP-RPA_len_noVnl | cp 02_IP-RPA_len/ndb.dipoles 02_IP-RPA_len_noVnl].

Notice that at this level we are considering linearly polarize light, polarization in the "x" direction

 % BLongDir
  1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
 % 

and thus we are computing [math]\displaystyle{ \epsilon_{xx}(\omega) }[/math].

To derive the absorption of circularly polarized light we need the off-diagonal component of the dielectric tensor εxy(ω). To this end, we need to compute the current-current response function, that is to move to the velocity gauge. Let's check how it works. Restore the [x,Vnl] DB,

 mv SAVE/hide_ns.kb_pp SAVE/ns.kb_pp

and then run yambo_kerr in the velocity gauge:

 yambo -F Inputs/02_IP-RPA_vel -J 02_IP-RPA_vel

The new input file differ from the last only for the variable

 Gauge= "length"              # [BSE] Gauge (length|velocity)
 ---
 Gauge= "velocity"            # [BSE] Gauge (length|velocity)

thus a different DB for the dipoles will be created (ndb.P_and_P2)

Compare the results of the three runs. The absence of the [x,Vnl] gives a significant change in the intensity of the absorption. The length and the velocity gauge formulation instead should be perfectly equivalent. They are if you are using a recent version of the code. The plot was, instead, generated with an earlier implementation, and the two results differ slightly. See

The full dielectric tensor and the Kerr effect

We are now ready to compute the off-diagonal component of the dielectric tensor. To this end, always in the directory withoutSO, run

 yambo -F Inputs/03_KERR_IP-RPA_vel -J 03_KERR_IP-RPA_vel

The only difference respect to the previous file is the presence of the logical

 BSEprop="abs kerr"              # [BSE] Compute the Kerr effect 

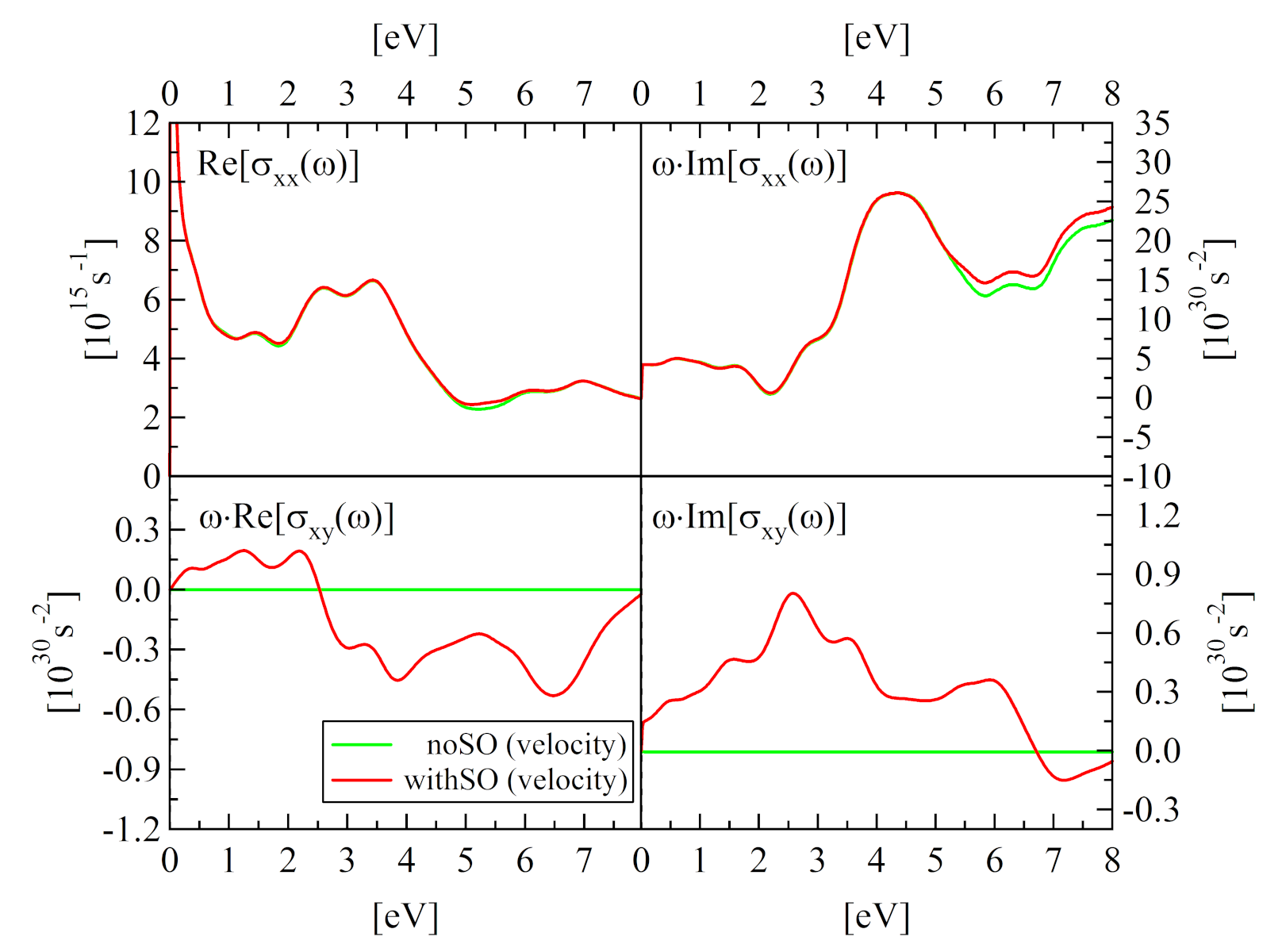
This time yambo will produce both the diagonal and the off-diagonal part of the dielectric tensor. We can plot them, both the real and the imaginary part. If you transform the dielectric tensor in the optical conductivity you should obtain a result similar to the following (green line): [Hint: use the value h=4.1356675 eV s to produce the plots remembering that the "x" axis of epsilon is in eV: x=ℏω.]

The off-diagonal components are almost zero. Indeed due to its cubic geometry, the dielectric tensor (and so the optical conductivity) of bulk iron without SO are diagonal. However you should have noticed that the real part of the off-diagonal component seems to diverge in the ω→0 limit. This is an exemple of the numerical instabilities of the velocity gauge...

Thus we now want to include the SO interaction. To this end we move in the withSO folder

 cd withSO 

and first initialise the DB,

 yambo -F Inputs/01_init 

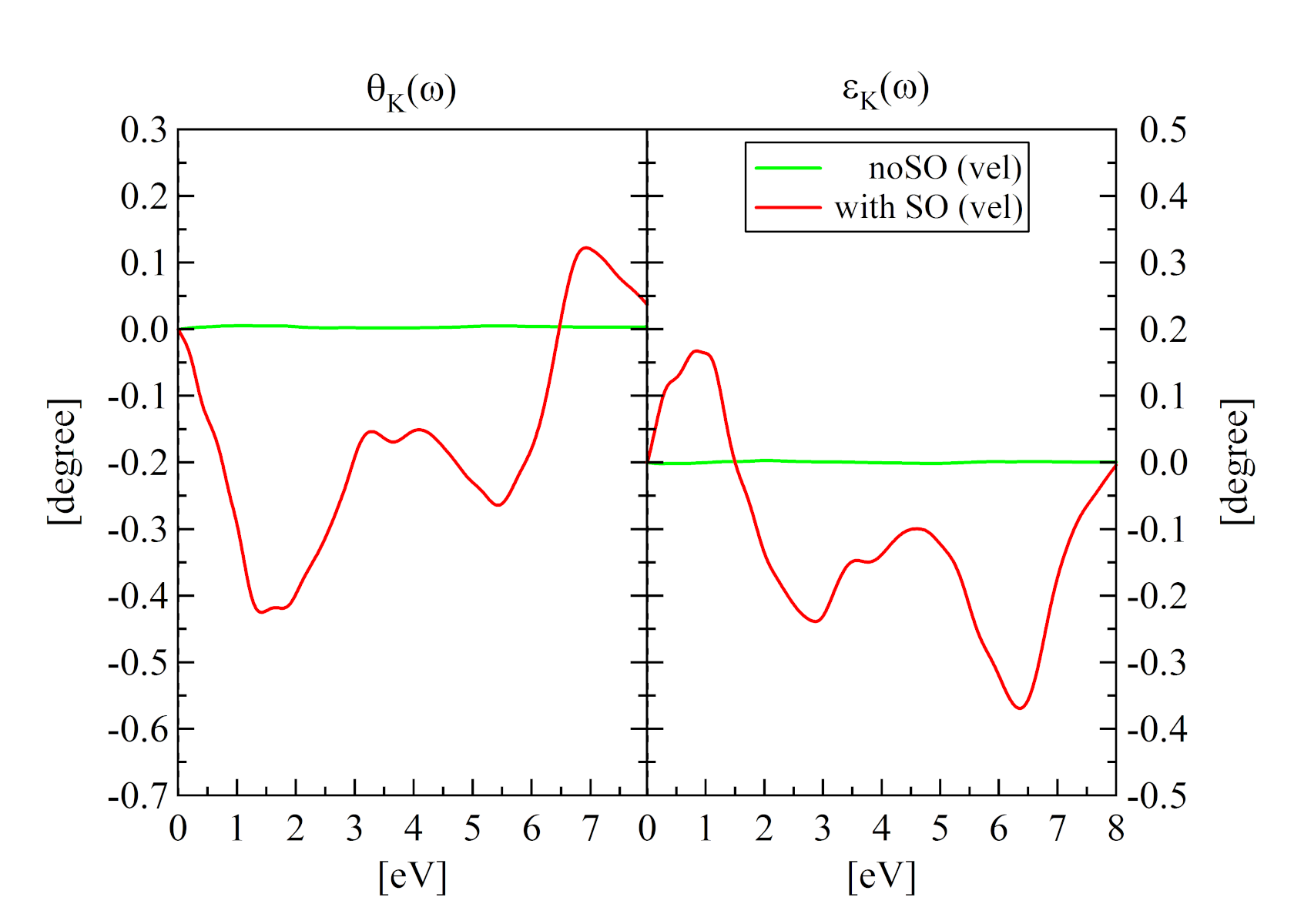
Now compute both the diagonal and the off-diagonal elements of the dielectric tensor, and the Kerr parameters. We just need to run

 yambo -F Inputs/02_KERR_IP-RPA_vel -J 02_KERR_IP-RPA_vel

and then plot the results which we can compare with the case without SO. The input file is identical to the previous one but now we are computing the epsilon starting from a DB with SO.

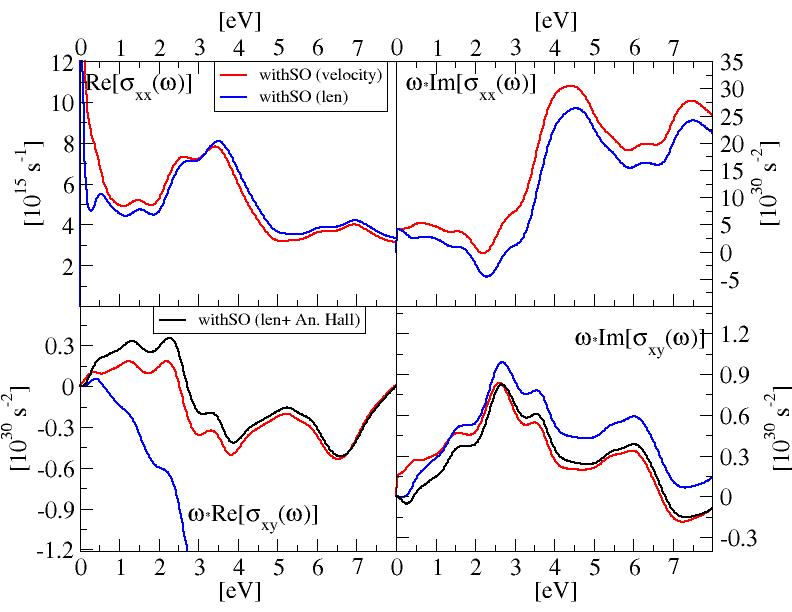
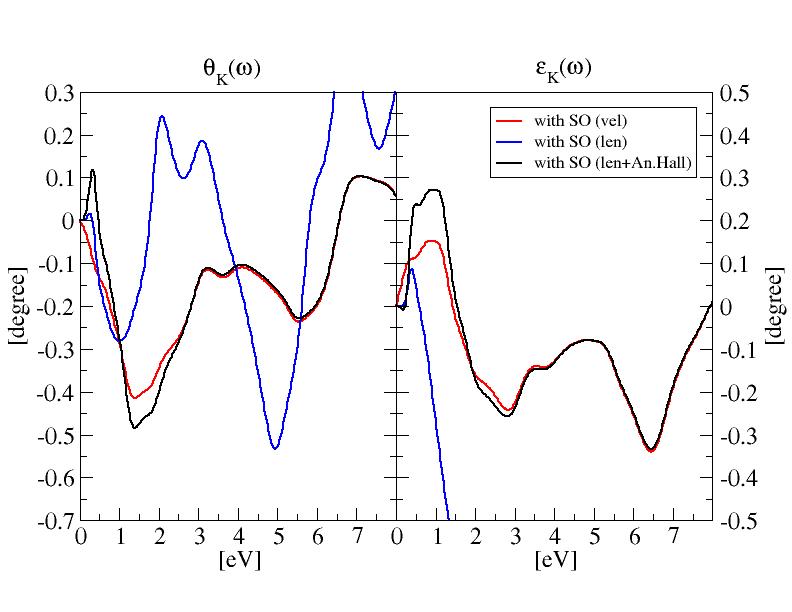
From the diagonal elements we see that SO is a very small effect in bulk iron but it is the only responsible for the off-diagonal part and thus for the MOKE.

The full dielectric tensor in the length gauge

The MOKE and more in general the absorption of circular polarized light can be described in the velocity gauge. However the equations for the velocity gauge suffer of numerical instabilities. While these is not a severe problem at the IP-RPA level, the instabilities could be more problematic with the inclusion of local fields or of the electron-hole interaction. Moreover the description of the full dielectric tensor in the velocity gauge requires the computation of the full current-current response function which cannot be obtained within a pure density based approach (indeed we are using yambo -o b and not yambo -o c). It is thus tempting to try to compute the MOKE in the more stable length gauge. To this end we use a generalized version of the equation for the lenght gauge, which however is formally not correct. Run

 yambo -F Inputs/03_KERR_IP-RPA_len -J 03_KERR_IP-RPA_len

and compare the results with the felocity gauge. The length expression is well defined for the diagonal part of the dielectric tensor which describes the optical absorption. The off-diagonal term however is not properly described with this approach.

However this difference can be traced back as due to a physical effect, the Anomalous Hall effect. Indeed if we add the expression for this term to the expression for the length gauge, thanks to the logical,

 AnHall                       # [BSE] Compute the anomalous Hall effect and if length add it to eps

and thus we run

 yambo -F Inputs/03_KERR_IP-RPA_len+AnHall -J 03_KERR_IP-RPA_len+AnHall

we finally obtain the correct result. The Anomalous Hall term is different from zero only in metals and in the so called Chern insulators, e.g. materials with non zero Chern number. In all other cases the length based approach is exact, at least at the IP-RPA level.

The two approaches mostly differ in the region ω→0.

Final Considerations

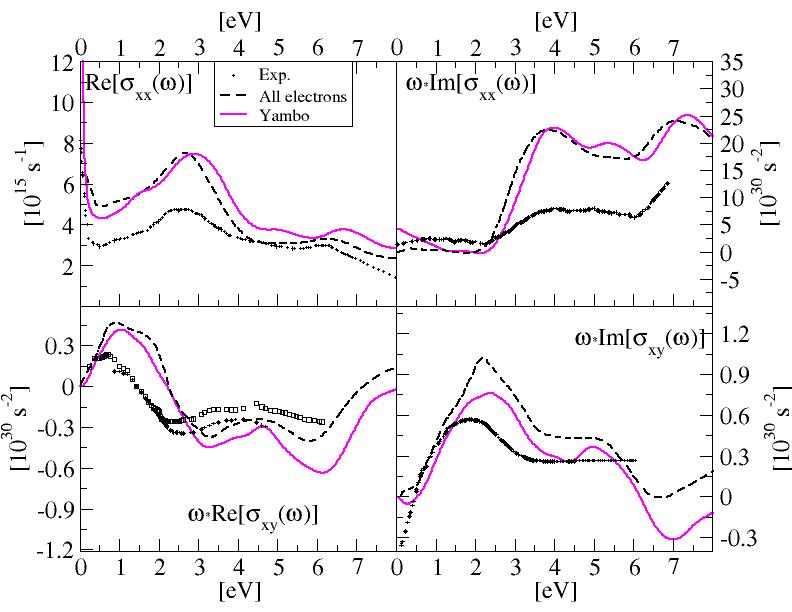
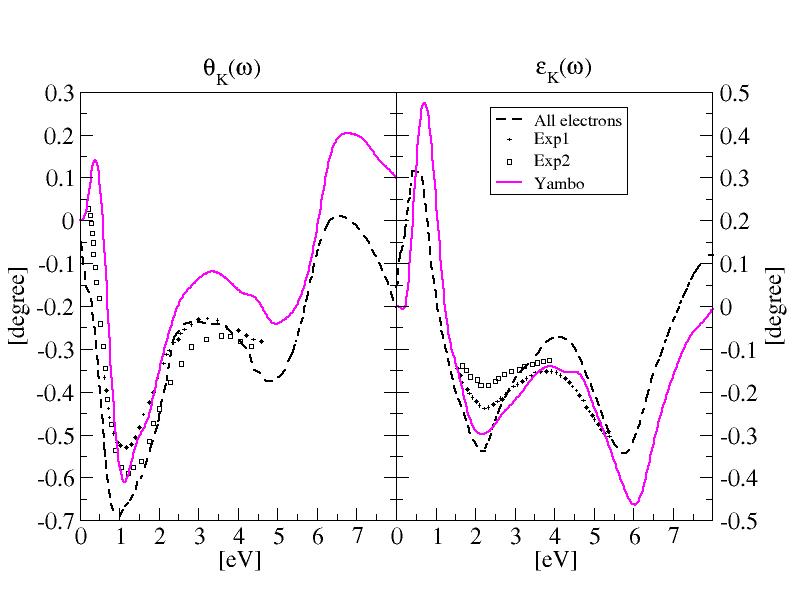
Remember that the spectra obtained in the present tutorial are from DBs with poor convergence parameters. Below you can find the results obtained with full convergence. Data published in Ref.. However you can notice that, already with the parameters used in the tutorial, the main features of the spectra

and of the Kerr parameters are already present.

All electrons theoretical calculations from Ref. and experimental data from references cited in the article.