Second-harmonic generation of 2D-hBN
Step 0: Theoretical framework
In this tutorial, we compute the Second-harmonic generation (SHG) from the dynamics of the Bloch-states. The equation-of-motion of the Bloch-states is explained in the tutorial on Linear response from Bloch-states dynamics. Independently of the 'experiment' we simulate, the part of the integration of motion stays the same. This means that any experiment, including non-linear optics, can be performed at the level of the theory listed for the computation of the dielectric function:
- independent (quasi)particle
- time-dependent Hartree (RPA level)
- time-dependent DFT (and DPFT)
- time-dependent Hartree+Screened exchange (BSE level)
What changes when we want to calculate the SHG (or higher harmonics) is:
- the time-dependence of the input electric field and
- the post-processing of the signal
Time dependence of the electric Field: we choose a sinusoidal electric field, thus a monochromatic laser field. This allows one to expand the polarization in the form [math]\displaystyle{ \bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{p}_n e^{-i\omega_n t} }[/math] where the coefficient [math]\displaystyle{ \bf{p}_1,...,\bf{p}_n }[/math] are related to [math]\displaystyle{ \chi^{(1)},...,\chi^{(n)} }[/math] through a coefficient depending on a power of the strength of the field (with the power depending on the order of the response).
At difference with a delta-like perturbation, a real-time simulation gives the response at the laser-field only. Then, to obtain the spectrum for the desired range of frequency, we have to perform so many simulations as the frequencies in the desired range.
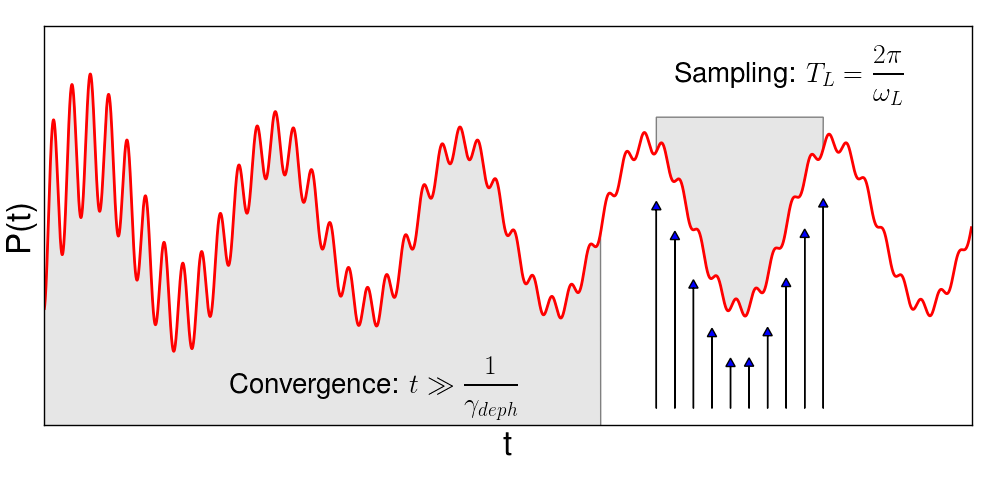
Post-processing of the signal: The switch-on of the electric field corresponds to a weak delta-like kick. Thus, even if it may not be noticeable, the polarization results from both the sinusoidal field and the delta-like kick. The latter excites all eigenfrequencies of the system. Though weak, the resulting signal is comparable with the second-harmonic signal. To eliminate the signal from the eigenfrequencies, we apply a dephasing ([math]\displaystyle{ \gamma_{deph} }[/math]). To have a signal useful to sample the second-harmonic signal, we need to wait a time [math]\displaystyle{ \bar t }[/math] much larger than the dephasing-time [math]\displaystyle{ 1/\gamma_{deph} }[/math]. Note that we cannot choose a too short dephasing time (to shorten the simulation time), as this would result in a too large broadening of the spectrum. After [math]\displaystyle{ \bar t }[/math], we sample $2N+1$ times in a period and use discrete Fourier transform to extract [math]\displaystyle{ {p}_n }[/math] for [math]\displaystyle{ n = 0,...,N }[/math], where n=2 gives the SHG. This is schematically illustrated in figure:
The scheme from Ref. [1] summarised the workflow for computing the SHG (or higher-harmonics) in a energy range [math]\displaystyle{ [\Omega_1,\Omega_2] }[/math].
Step 1: Prerequisites
In this example, we will consider a single layer of hexagonal boron nitride (hBN). Before running real time simulations to compute the SHG in yambo you need to:
- download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz.
- perform the steps described in Prerequisites for Real Time propagation with Yambo.
- complete the Dielectric function from Bloch-states dynamics tutorial.
REVISE THE ABOVE IF USING SOME DIFFERENT DATABASE
Step 2: Independent-particle approximation
Use the command:
yambo_nl -u -F Inputs_shg/01_td_ip.in
to generate the input (NOTE THIS IS A PLACEHOLDER):
nloptics # [R NL] Non-linear optics NL_Threads= 1 # [OPENMP/NL] Number of threads for nl-optics % NLBands 3 | 6 | # [NL] Bands % NLstep= 0.0100 fs # [NL] Real Time step length NLtime=55.000000 fs # [NL] Simulation Time NLverbosity= "high" # [NL] Verbosity level (low | high) NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.200000 | 8.000000 | eV # [NL] Energy range % NLEnSteps= 1 # [NL] Energy steps NLDamping= 0.000000 eV # [NL] Damping % ExtF_Dir 0.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor % ExtF_kind= "DELTA" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
ADD A DESCRIPTION OF THE MAIN PARAMETERS, LINKING THEM WITH THE THEORETICAL PART
Run the simulation:
yambo_nl -F Inputs_shg/01_td_ip.in -J TD-IP_nl -C TD-IP_nl
TO DO: The run now is performing a real-time simulation per frequency, and therefore it takes approximately X times more time than the linear response simulation (NB check as well length of the simulation and amend)
TO DO: Add a plot of the polarization. Note that it is sinusoidal etc. and the nonlinear part is not visible since every order is as a rule of a thumb 6-7 orders of magnitude smaller than the previous.
Output post-processing: the dielectric function
Once we obtained the polarization, we Fourier-transform the polarization to obtain the dielectric function.
Use the command:
ypp_nl -u -F Inputs_shg/ypp_shg.in
to generate the input file (THIS IS A PLACEHOLDER):
nonlinear # [R] NonLinear Optics Post-Processing Xorder= 1 # Max order of the response functions % TimeRange -1.000000 |-1.000000 | fs # Time-window where processing is done % ETStpsRt= 1001 # Total Energy steps % EnRngeRt 0.00000 | 10.00000 | eV # Energy range % DampMode= "LORENTZIAN" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) DampFactor= 0.10000 eV # Damping parameter
TO-DO: describe the main keys and parameters.
To run the post-processing, use the command:
ypp_nl -F Inputs_shg/ypp_shg.in -J TD-IP_nl -C TD-IP_nl
TO-DO describe which files are produced
TO-DO: Plot the SHG and comments
Step 3: Hartree+Screened exchange approximation (BSE level)
References
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)