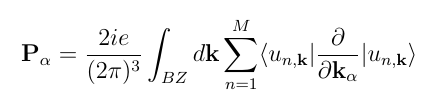Dielectric function from Bloch-states dynamics
Step 0: Theoretical background
The dynamics of Bloch-states is found by integrating a set of Time Dependent Effective Schrödinger Equations (TD-ESEs). Effective means that an effective Hamiltonian is considered. We consider the many-body effective Hamiltonians seen in the Linear response from real time simulations. In addition, one can also consider effective Hamiltonians based on density-functional theory. The latter choice gives time-dependent density-functional theory.
At difference with what seen in Linear response from real time simulations, the coupling between electrons and the external field is described by means of the Modern Theory of Polarization:
Where [math]\displaystyle{ | v_{i \mathbf{k}} \rangle }[/math] are the time-dependent valence bands, [math]\displaystyle{ H_{rt} }[/math] is the Hamiltonian, [math]\displaystyle{ \mathcal E(t) }[/math] is the external field and the term [math]\displaystyle{ i e \partial k }[/math] corresponds to the dipole operator in periodic systems. For more details on this last term see Ref. [1] and [2].
The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response, we probe the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transforms.
The hamiltonian is defined as in the case of the equation of motion for the density matrix. Then the polarization is calculated by means of Berry's phase
Note that the equations of motion of Yambo are in the length gauge. Other codes choose instead to work in the velocity gauge. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of Ref. [3].
- ↑ I. Souza, J. Íñiguez, and D. Vanderbilt, PRB 69, 085106 (2004)
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)
- ↑ C. Attaccalite, arXiv 1609.09639 (2017)