Yambopy tutorial: band structures
This tutorial will show you how to visualise wave-function and band-structure related information following a DFT Quantum Espresso calculation using the "qepy" module of Yambopy.
The full tutorial, including the Quantum espresso and Yambo databases that we will read, can be downloaded and extracted from the yambo website:
$wget www.yambo-code.org/educational/tutorials/files/databases_qepy.tar $tar -xvf databases_qepy.tar $cd databases_qepy
Tutorial 1. BN (semiconductor). Band structure
The qepy classes are useful both to execute Quantum Espresso and to analyze the results. The full qepy library is imported by simply doing:
from qepy import *
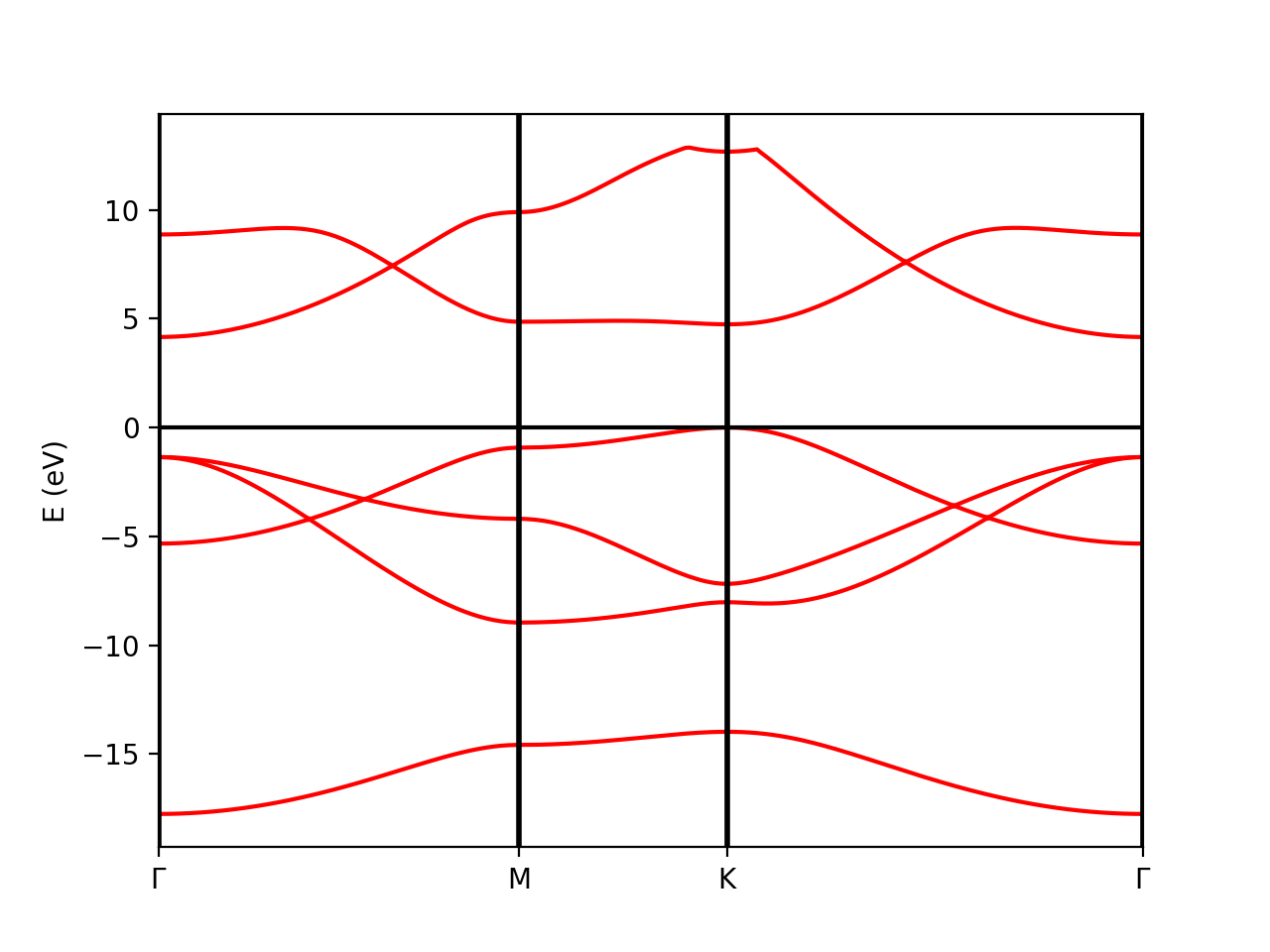
Plot Band structure
The qepy class PwXML reads the data file generated by Quantum Espresso and post-processes the data. The class is instanced by doing:
xml = PwXML(prefix='bn', path='bands')
The variable prefix corresponds to the same variable of the QE input. The folder location is indicated by variable path. In order to plot the bands, we also define the k-points path (in crystal coordinates) using the function Path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0],'$\Gamma$'],
[[0.5, 0.0, 0.0],'M'],
[[1./3,1./3,0.0],'K'],
[[0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)])
It is worth to note that the path should coincide with the selected path for the QE band calculations.
In order to show the plot we call the plot_eigen method of the PwXML class:
xml.plot_eigen(path_kpoints)
This function will automatically plot the bands as shown below running the script:
python plot-qe-bands.py
Alternatively, we can use the function plot_eigen_ax. This functions requires as input a matplotlib figure object with given axes, as you will see in the next example.
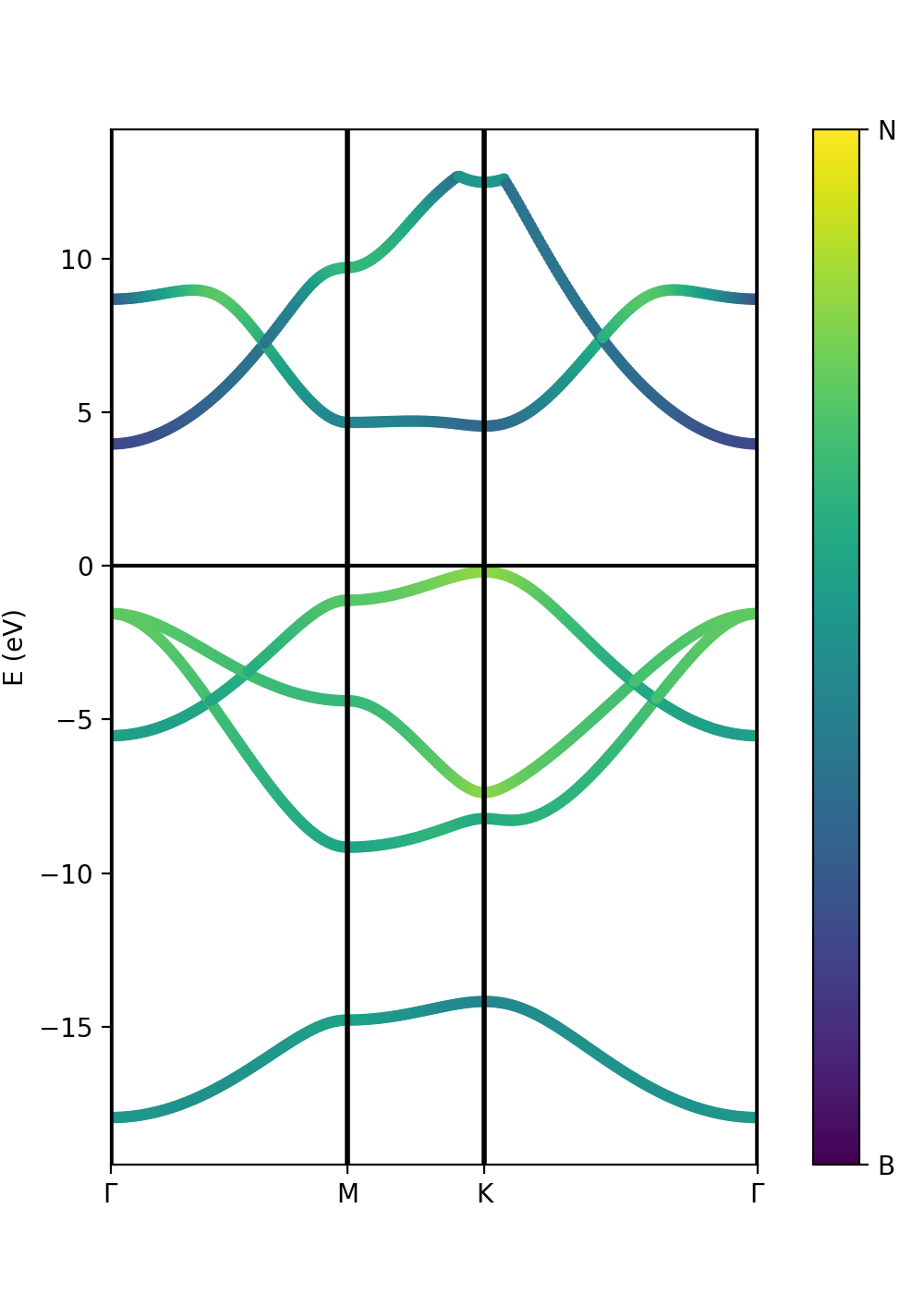
Plot atomic orbital projected Band structure
In addition to the band structure, useful information regarding the atomic orbital nature of the electronic wave functions can be displayed using the class ProjwfcXML. In order to make quantum espresso calculate the relevant data, we need to use the QE executable projwfc.x, which will create the file atomic_proj.xml. This executable projects the Kohn-Sham wavefunctions onto orthogonalized atomic orbitals, among others functionalities. The orbital indexing and ordering are explained in the input documentation of the projwfc.x function which you are invited to check (https://www.quantum-espresso.org/Doc/INPUT_PROJWFC.html#idm94). We can projwf.x directly from the python script using the qepy class ProjwfcIn:
proj = ProjwfcIn(prefix='bn') proj.run(folder='bands')
Be aware that this can take a while in a large system with many k-points. As in the class PwXML, we then define the path_kpoints and also the selected atomic orbitals to project our bands. We have chosen to represent the projection weight onto the boron (1) and nitrogen (2) orbitals, which according to the projection orderings is given by
atom_1 = list(range(16)) atom_2 = list(range(16,32))
The full list of orbitals is written in the file bands/prowfc.log. We have also defined the figure box
import matplotlib.pyplot as plt fig = plt.figure(figsize=(5,7)) ax = fig.add_axes( [ 0.12, 0.10, 0.70, 0.80 ])
The class ProjwfcXML then runs as in this example:
band = ProjwfcXML(prefix='bn',path='bands',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',selected_orbitals=atom_1,selected_orbitals_2=atom_2)
We can run now the file:
python plot-qe-orbitals.py
We have chosen the colormap 'viridis' (variable cmap). You see that the colormap goes from maximum selected_orbitals content (in this case boron) to the maximum selected_orbitals_2 content (in this case nitrogen). The colormap can be represented in many ways and qepy does not include a particular function for this. An example is:
import matplotlib as mpl
cmap=plt.get_cmap('viridis')
bx = fig.add_axes( [ 0.88, 0.10, 0.05, 0.80 ])
norm = mpl.colors.Normalize(vmin=0.,vmax=1.)
cb1 = mpl.colorbar.ColorbarBase(bx, cmap=cmap, norm=norm,orientation='vertical',ticks=[0,1])
cb1.set_ticklabels(['B', 'N'])
We can also plot the band orbital charater with size variation instead of a color scale. In this case we have to pass only the variable selected_orbitals (see the next tutorial).
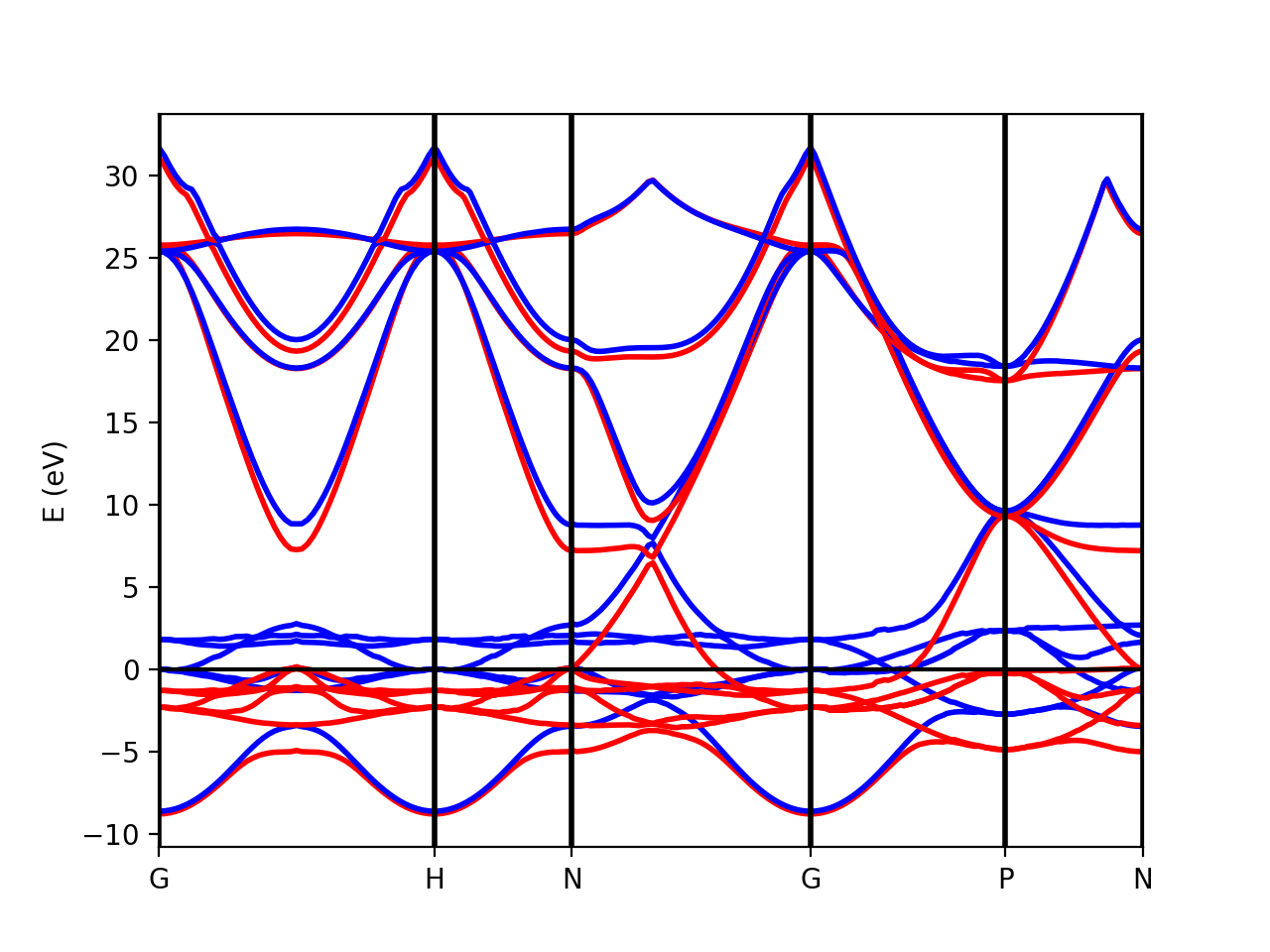
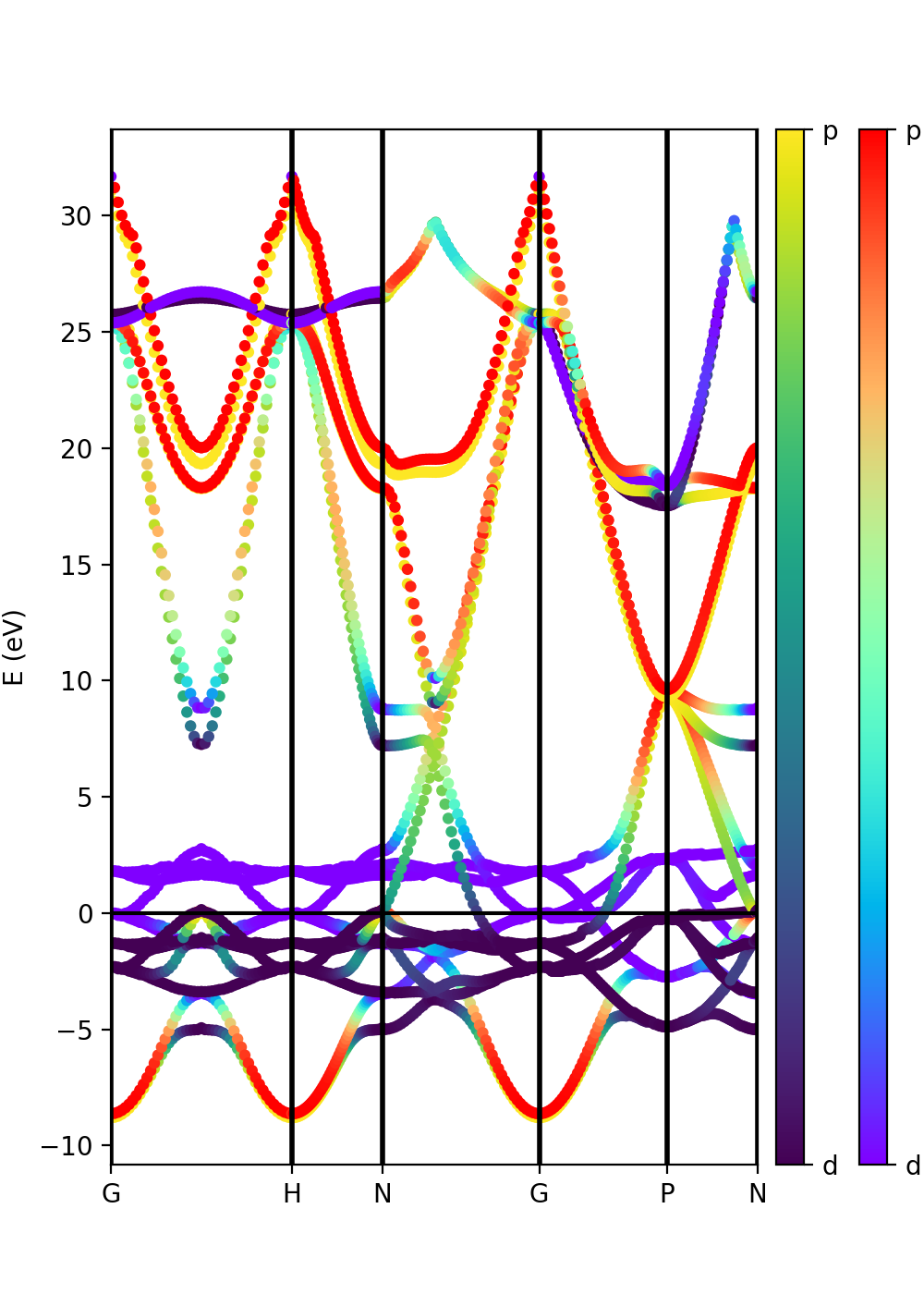
Tutorial 2. Iron. Ferromagnetic metalic material
In the case of spin-polarized calculations we can plot the spin up and down band structures. We have included in the tutorial the example of using the Classes Tasks and Flows developed in yambopy. You can check the file flow-iron.py to check an example. Yambopy includes basic predefined workflows to run the common QE and Yambo calculations. In this case we are using the class PwBandsTasks.
python flow-iron.py
In order to plot the spin-polarized bands. We have to run the file:
python plot-qe-bands.py
The class PwXML automatically detects the spin polarized case (nspin=2 in QE input file). The spin up channel is displayed with red and the spin down channel with blue. In the case of iron we have selected this path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0 ],'G'],
[[0.0, 0.0, 1.0 ],'H'],
[[1./2,0.0,1./2.],'N'],
[[0.0, 0.0, 0.0 ],'G'],
[[1./2, 1./2, 1./2 ],'P'],
[[1./2,0.0,1./2. ],'N']], [npoints,npoints,npoints,npoints,npoints])
xml = PwXML(prefix='pw',path='bands/t0') xml.plot_eigen(path_kpoints)
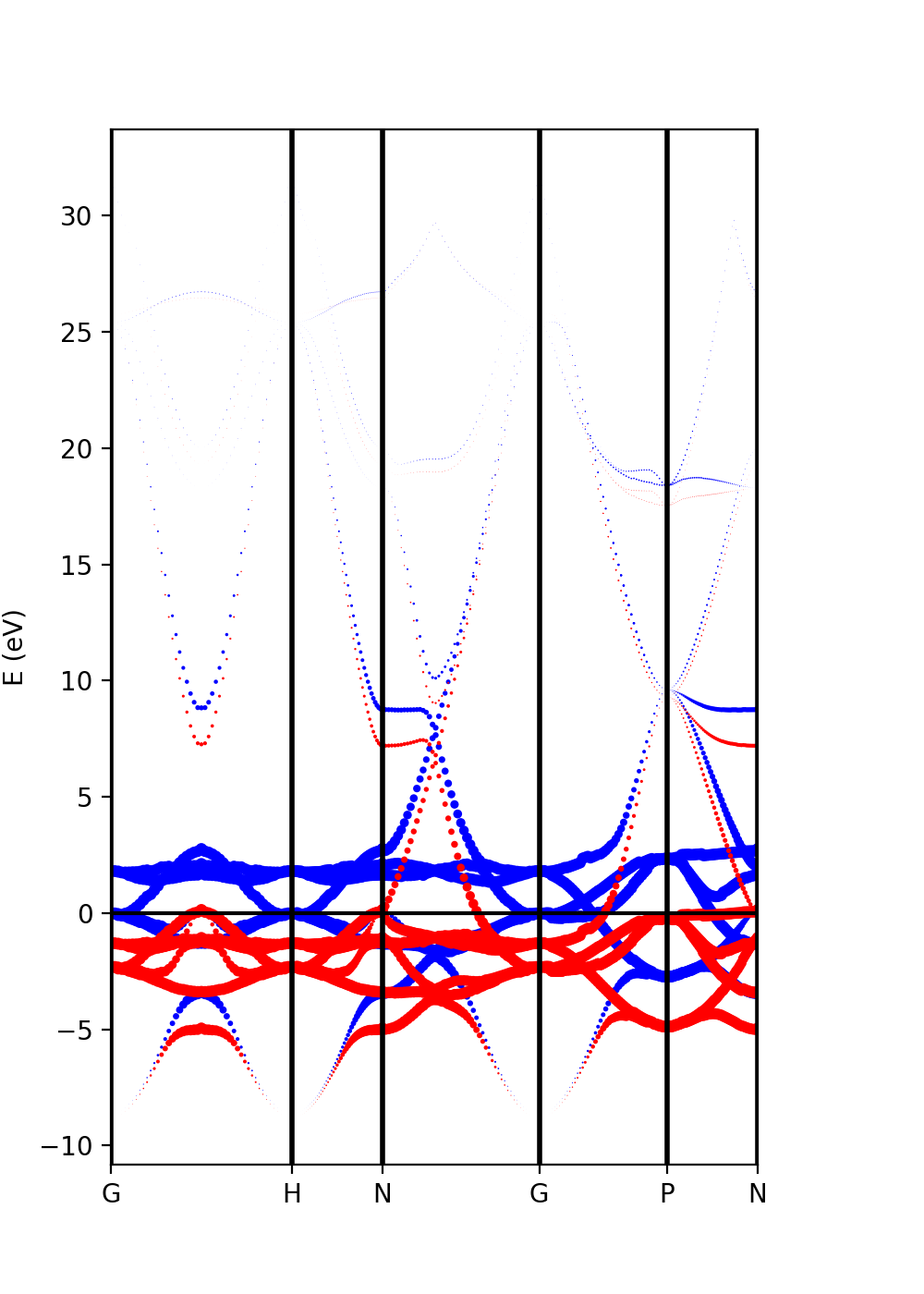
The analysis of the projected atomic orbitals is also implemented. In this case the results are more cumbersome because the projection is separated in spin up and down channels. In the case of representing the size as a function of the weight of the orbitals, we have represented exclusively the d orbitals:
atom_d = [3,4,5,6,7] band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,selected_orbitals=atom_d,color='red',color_2='blue')
If we run the file:
plot-qe-orbitals-size.py
From the plot is clear that d orbitals are mainly localized around the Fermi energy.
Another option is to plot the orbital composition as a colormap running the file:
plot-qe-orbitals-colormap.py
Here we have added the p and d orbitals in the analysis:
atom_p = [0,1,2] atom_d = [3,4,5,6,7] band = ProjwfcXML(prefix='pw',path='bands/t0',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',cmap2='rainbow',selected_orbitals=atom_p,selected_orbitals_2=atom_d)
The colormap bar is added in the same way as in Tutorial 1 (see script).
Tutorial 3
Yambopy is used mainly to run Yambo and QE calculations. Nevertheless, there are classes to analyse the results of Yambo and deals with the database generated by Yambo. In the case of GW quasi-particle calculations we can use the class YamboQPDB to find the scissor operator, plot the GW bands and to interpolated the GW bands in a smoother k-path. The example runs by doing:
python plot-qp.py
See below for an explanation of the tutorial. As usual, we can import the qepy and yambopy libraries:
from qepy import * from yambopy import * import matplotlib.pyplot as plt
We define the k-points path.
npoints = 10
path = Path([ [[ 0.0, 0.0, 0.0],'$\Gamma$'],
[[ 0.5, 0.0, 0.0],'M'],
[[1./3.,1./3., 0.0],'K'],
[[ 0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)] )
Importantly, the number of points is a free choice. We can increase the variable npoints as we wish, just the interpolation will take more time. In order to analyse GW results we need to have the file related to the basic data of our Yambo calculation (SAVE/ns.db1) and the netcdf file with the quasi-particle resutls (ndb.QP). We load the data calling the respective classes:
# Read Lattice information from SAVE lat = YamboSaveDB.from_db_file(folder='SAVE',filename='ns.db1') # Read QP database ydb = YamboQPDB.from_db(filename='ndb.QP',folder='qp-gw')
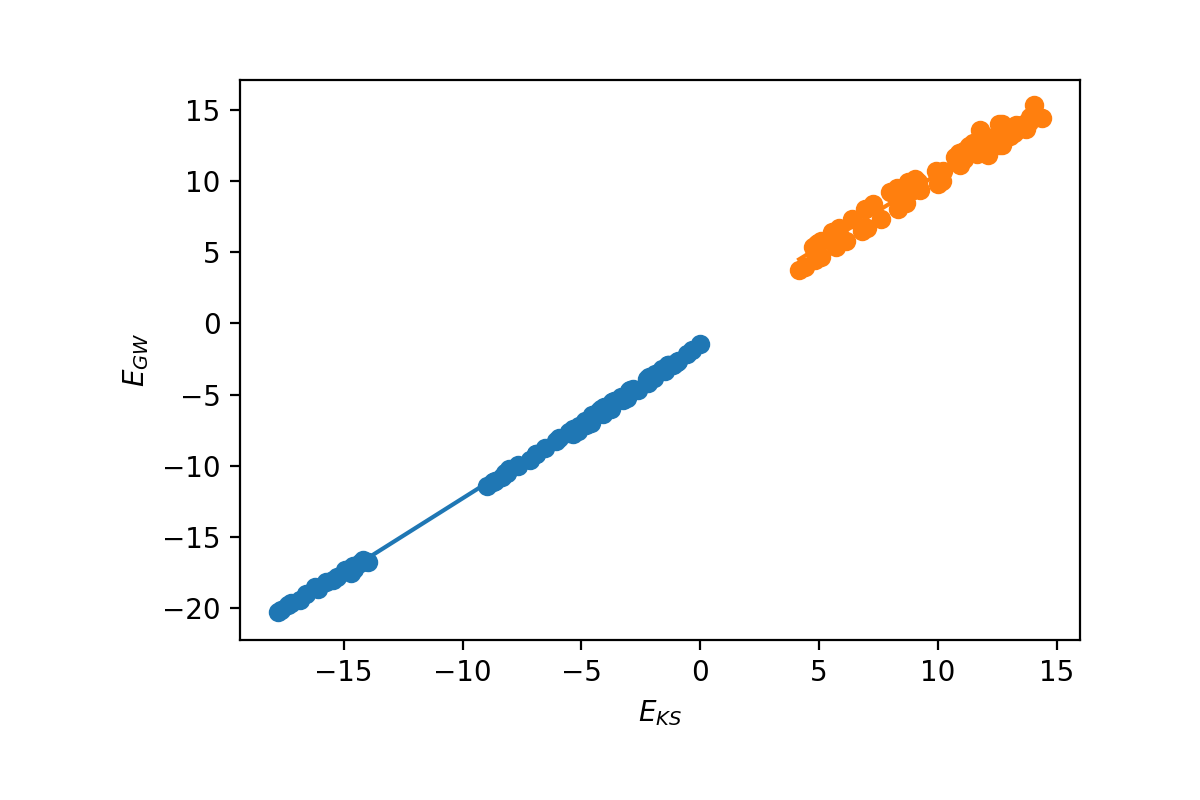
The first option is to plot and calculate the scissor operator. We need to select the index of the top valence band:
n_top_vb = 4 ydb.plot_scissor_ax(ax,n_top_vb)
Yambopy displays the fitting and also the data of the slope of each fitting. Notice that this is also a test if the GW calculations are running well. If the dependence is not linear would be very rare and you should double-check your results!
In this case the slope is:
valence bands: slope: 1.0515886598785766 conduction bands: slope: 1.026524081134514 scissor list (shift,c,v) [eV,adim,adim]: [1.8985204833551723, 1.026524081134514, 1.0515886598785766]
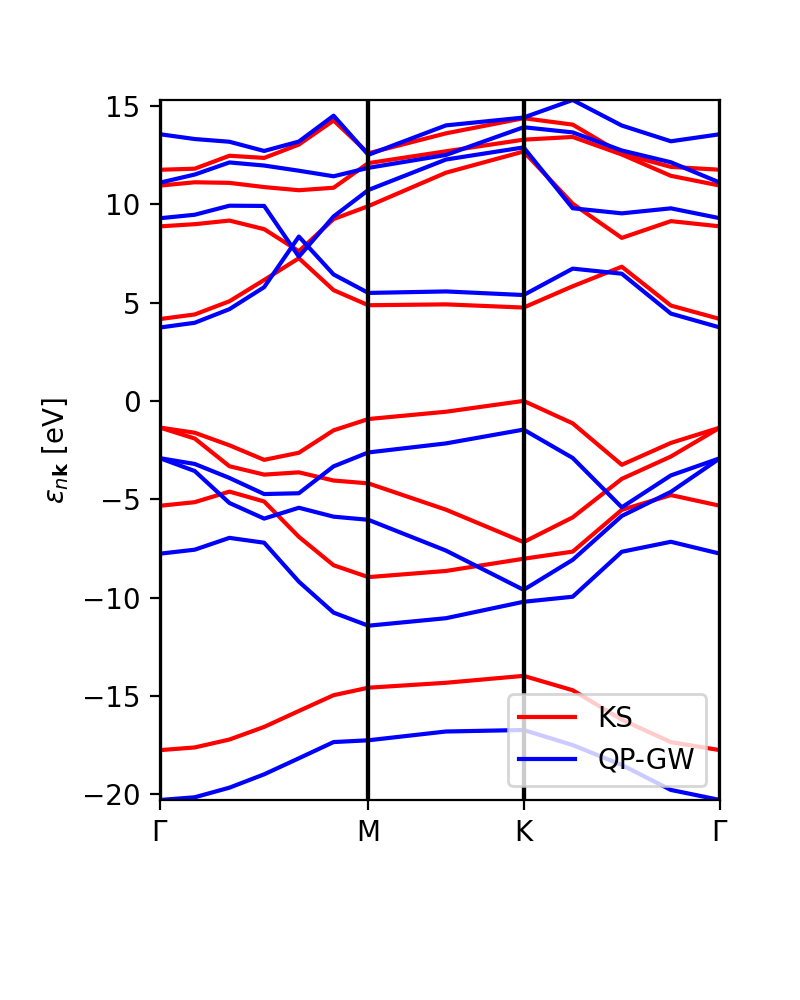
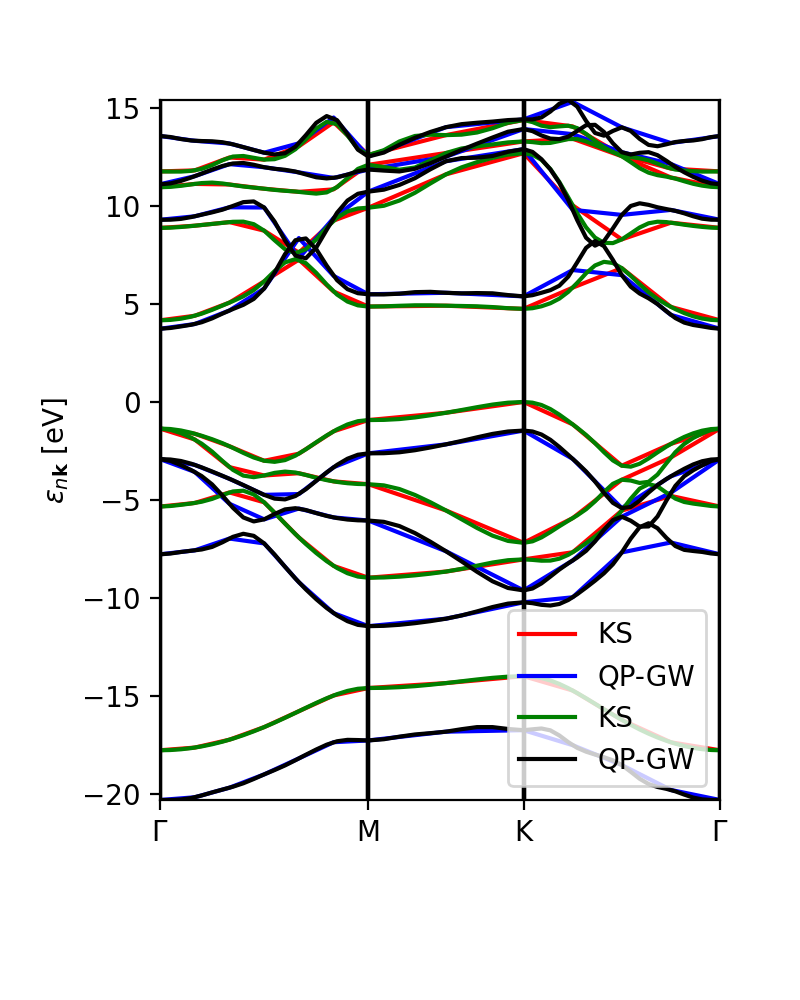
In addition to the scissor operator, we can plot the GW (and DFT) band structure, in the path. The first choice would be to plot exact GW calculations, without interpolation, to check that the results are meaningfull (or not). This plot is independent of the number of k-points (npoints) that we want to plot in the interpolation. The class YamboQPDB finds the calculated points that belong to the path and plot them. Be aware that if we use coarse grids the class would not find any point and the function will not work.
ks_bs_0, qp_bs_0 = ydb.get_bs_path(lat,path) ks_bs_0.plot_ax(ax,legend=True,color_bands='r',label='KS') qp_bs_0.plot_ax(ax,legend=True,color_bands='b',label='QP-GW')
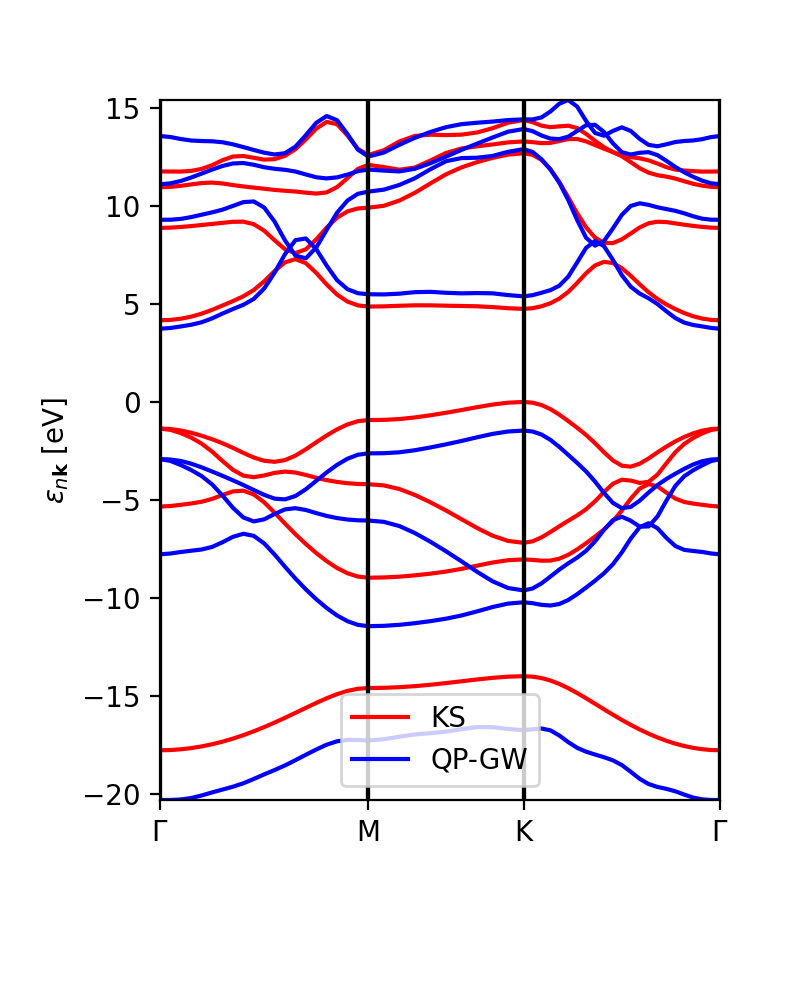
The interplation of the DFT and GW band structures has a similar aspect:
ks_bs, qp_bs = ydb.interpolate(lat,path,what='QP+KS',lpratio=20) ks_bs.plot_ax(ax,legend=True,color_bands='r',label='KS') qp_bs.plot_ax(ax,legend=True,color_bands='b',label='QP-GW')
The lpratio can be increase if the interpolation does not work. The interpolation is the one implemented by abipy.
Finally, we can compare the calculated GW eigenvalues with the interpolation.
Links
- Back to ICTP 2022#Tutorials