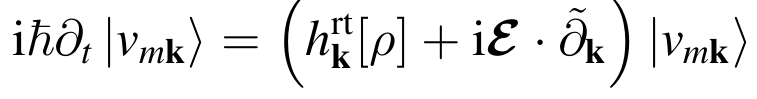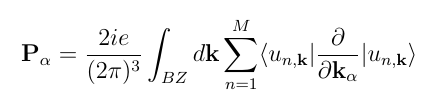Real time approach to linear response

Background

The Yambo code implements a real-time effective Schrödinger Equation(TDSE), where the coupling between electrons and the external field is described by means of the Modern Theory of Polarization:

Where [math]\displaystyle{ | v_{i \mathbf{k}} \rangle }[/math] are the time-dependent valence bands, Hsysk is the Hamiltonian, [math]\displaystyle{ \mathcal E(t) }[/math] is the external field and the term [math]\displaystyle{ i e \partial k }[/math] corresponds to the dipole operator in periodic systems. For more details on this last term see Ref. and . Differently from other codes, the equations of motion of Yambo are in the length gauge and not in the velocity one. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of Ref. . The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response, we probe the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transforms. We calculate the Berry polarization

and from its Fourier transform we get the linear response, see Ref. .

Prerequisites

The real-time response using the Time-Dependent Schroedinger Equation(TDSE) needs yambo_nl and ypp_nl in double precision. In order to compile it, just add the flag --enable-dp in your configure. If you have problems in the compilation please have a look to compiling yambo.

You can download input files and Yambo databases for this tutorial here: hBN-2D.

This tutorial on TDSE is divided into 8 steps:

DFT calculations

In this example, we will consider a single later of hexagonal boron nitride (hBN). The first input file is a self-consistent(SCF) calculation that is used to generate the density of the system. The second input file is a non-self consistent(NSCF) calculation to diagonalize the KS Hamiltonian, which depends on the density of the first run, on for a given number of bands and k-points. Notice that parameters in the NSCF calculation determine the number of k-points and the maximum number of bands that can be used in Lumen. Run this calculation with the command:

pw.x -inp hBN_2D_scf.in  > output_scf
pw.x -inp hBN_2D_nscf.nscf.in > output_nscf

Notice that in the NSCF file of QuantumEspresso we use the flag force_symmorphic=.true. to exclude the non-symmorphic symmetries that are not supported by Yambo.

Import the wave-functions

If you used QuantumEspresso go in the folder hBN_2D.save. Then import the wave-function with the command

for QuantumEspresso: p2y -F data-file.xml

Setup

Generate the setup input file with the command yambo_nl -i -V RL -F setup.in, then run yambo_nl -F setup.in. You can reduce the number of G-vectors in the setup in such a way to speed up calculations. I advise reducing G-vector to 1000 (about 50% of the initial ones).

Reduce symmetries

Since in real-time simulation we introduce a finite electric field in the Hamiltonian, the number of the symmetries of the original system is reduced due to the presence of this field. Using the tool ypp -y to generate the input file:

fixsyms                      # [R] Reduce Symmetries
% Efield1
 0.00     | 1.00     | 0.00     |        # First external Electric Field
%
% Efield2
 0.00     | 0.00     | 0.00     |        # Additional external Electric Field
%
#RmAllSymm                   # Remove all symmetries
RmTimeRev                    # Remove Time Reversal

Set the external field in the y-direction and uncomment the Time Reversal flag, as shown in red above. Run ypp and it will create a new folder called FixSymm with the reduced symmetries wave-functions.

Setup again

Go in the FixSymm directory and run the setup again yambo_nl -F ../setup.in. Now everything is ready for the real-time simulations!

Real-time dynamics

In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field. Use the command yambo_nl -u -F input_lr.in to generate the input:

nlinear                      # [R NL] Non-linear optics
NL_Threads= 1                # [OPENMP/NL] Number of threads for nl-optics
% NLBands
  3 |  6 |                   # [NL] Bands
%
NLstep=   0.0100       fs    # [NL] Real Time step length
NLtime=55.000000      fs    # [NL] Simulation Time
NLverbosity= "high"           # [NL] Verbosity level (low | high)
NLintegrator= "INVINT"       # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "IPA"         # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF")
NLLrcAlpha= 0.000000         # [NL] Long Range Correction
% NLEnRange
 0.200000 | 8.000000 | eV    # [NL] Energy range 
%
NLEnSteps= 1                 # [NL] Energy steps
NLDamping= 0.000000    eV    # [NL] Damping
% ExtF_Dir
 0.000000 | 1.000000  | 0.000000 |        # [NL ExtF] Versor
%
ExtF_kind=  "DELTA"          # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)

The standard input of Lumen is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red. We set the verbosity to "high" in such a way to print real-time output files. We set the differential equation integrator to INVINT that is faster but less accurate than the default (see Ref. ) . This integrator is ok in case of independent partcicles but I advise you to use CRANKNIC integrator when correlation effects are present. 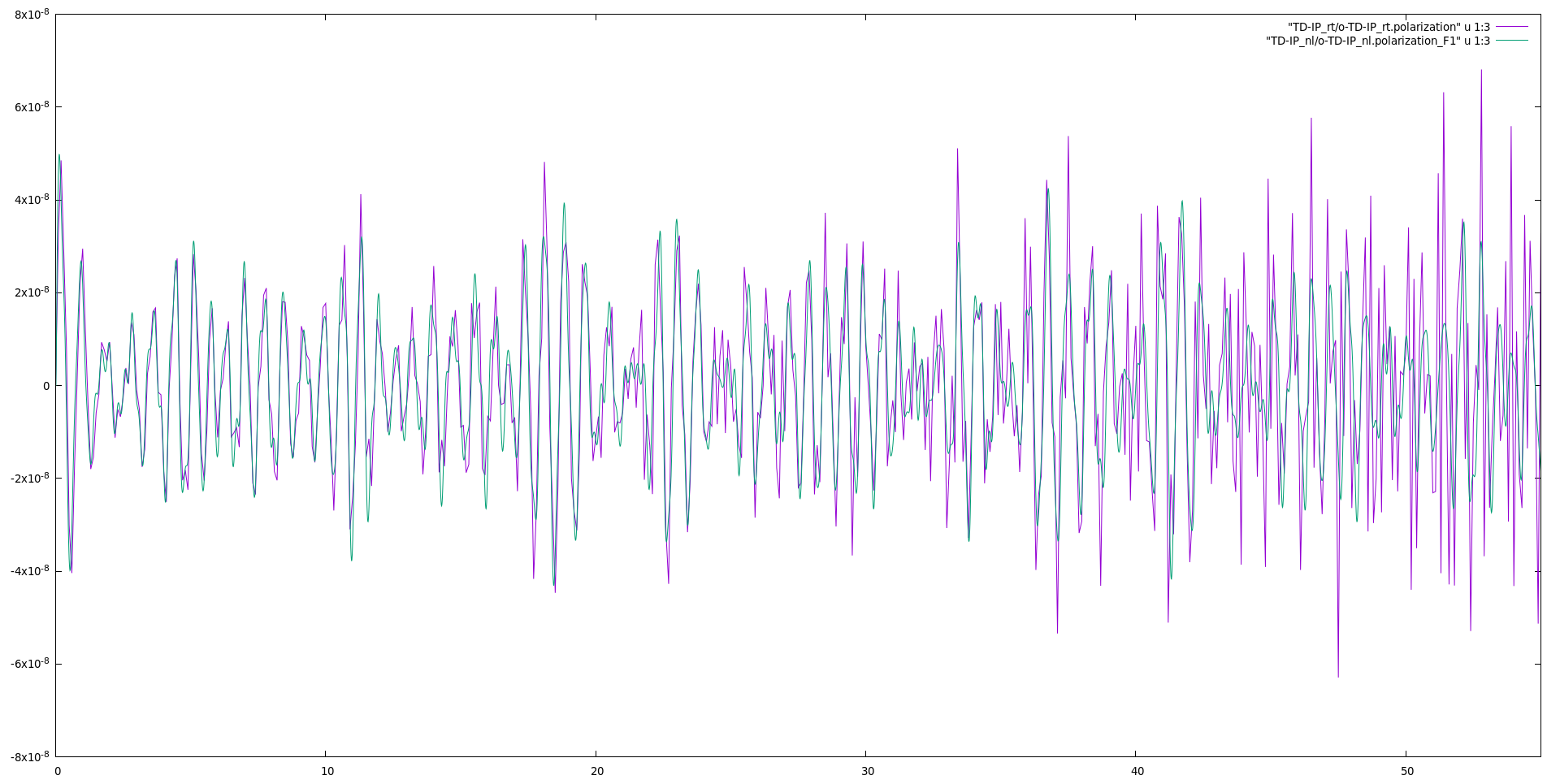Now run yambo_nl -F input_lr.in The code will produce different files: o.polarization_F1 that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. If you plot the third column of o.polarization_F1 versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:

Results Analysis

Now we can use ypp_nl -u to analyze the results:

nonlinear                    # [R] NonLinear Optics Post-Processing
Xorder= 1                    # Max order of the response functions
% TimeRange
-1.000000 |-1.000000 | fs    # Time-window where processing is done
%
ETStpsRt= 200                # Total Energy steps
% EnRngeRt
  0.00000 | 10.00000 | eV    # Energy range
%
DampMode= "LORENTZIAN"             # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor=  0.10000   eV    # Damping parameter

where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result. Then we run ypp_nl and obtain the following files: the dielectric constant along with the field direction o.YPP-eps_along_E, the EELS along with the same direction o.YPP-eels_along_E, and the damped polarization o.YPP-damped_polarization. 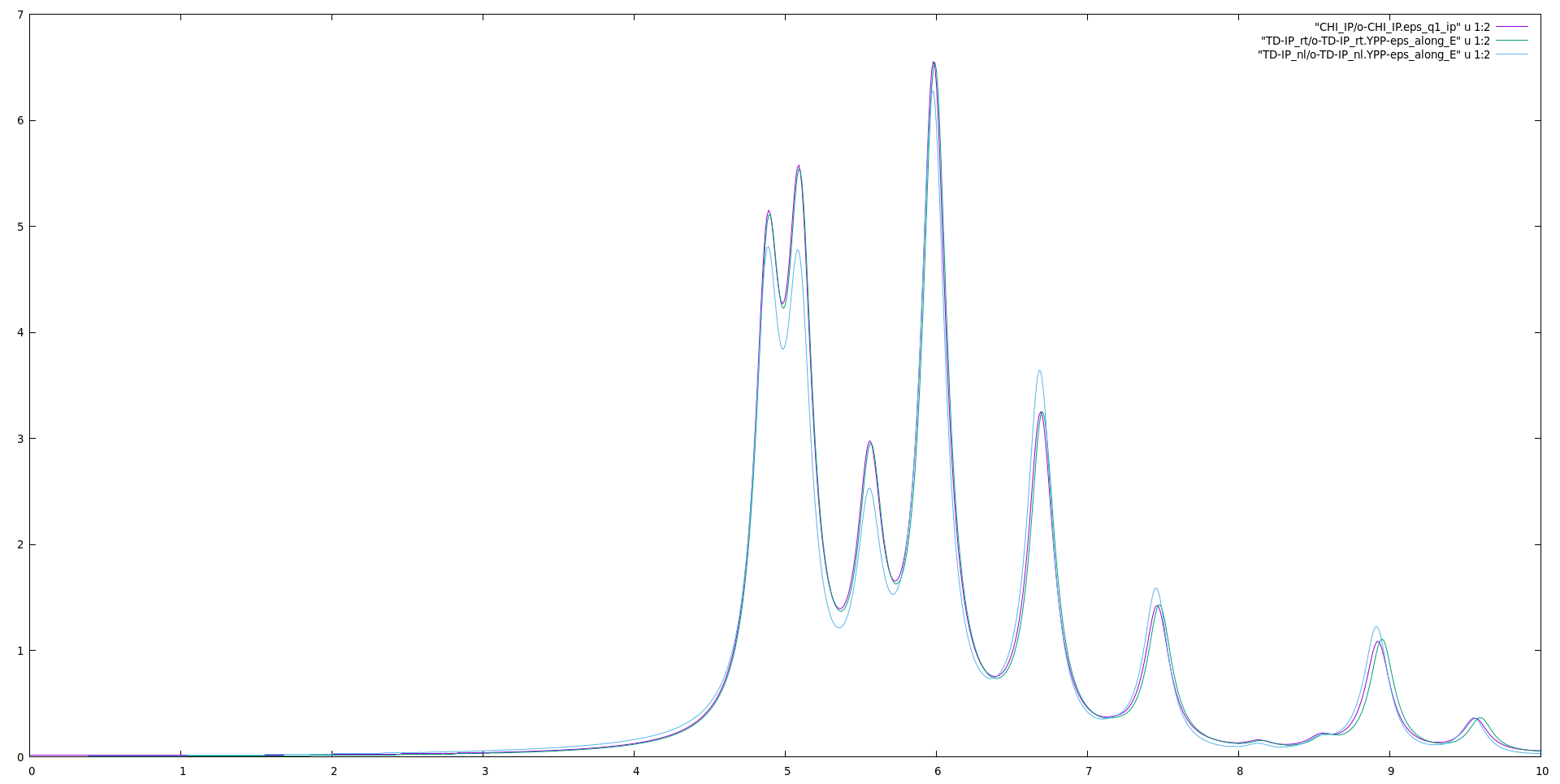Now we can plot the dielectric constant and compare it with the linear response:

The input for the linear response can be downloaded here. Notice that in a real-time simulation we obtain directly the

[math]\displaystyle{ \chi(\omega) = \frac{P(\omega)}{E(\omega)} }[/math]

that is realted to the dielectric constant throught the relation [math]\displaystyle{ \epsilon(\omega) = 1 + 4 \pi \chi(\omega) }[/math]