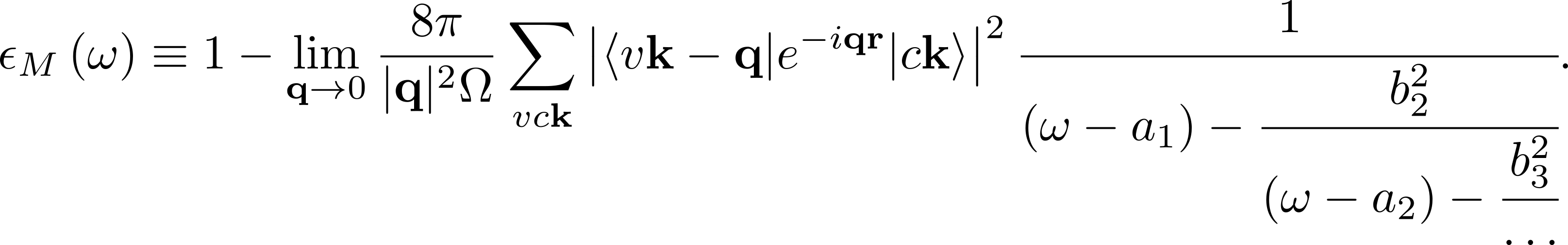Bethe-Salpeter solver: Lanczos-Haydock

You can avoid the full matrix diagonalization (which rapidly become expensive as it scales as N³) by using the Lanczos-Haydock solver mentioned above. While for small matrices these two methods have similar computational cost, for matrices of the size 10000 by 10000 and larger, the Haydock solver is remarkably faster. The drawback is that excitonic functions cannot be calculated. Within the Lanczos-Haydock approach the macroscopic dielectric function is rewritten as continued fraction

where a 's and b 's result from the Lanczos iterative algorithm.

To use the Lanczos-Haydock solver invoke yambo with "-y h" option in the command line:

$ yambo -y h -F 03_3D_BSE_haydock_solver.in

Beside the same input parameters defined for the diagonalization solver, the parameter

BSHayTrs= -0.02000          

defines the threshold accuracy for the Lanczos-Haydock iterative process: the calculation stops when the difference between two consecutive calculated spectra is smaller than the absolute value of the threshold. The minus sign indicates that the average difference over the specified energy range is considered (i.e. that means that cancellations of error may occur) as opposed to the maximum absolute difference over the specified energy range (plus sign). For the moment we leave this variable unchanged. This parameter ultimately determines the terms are included in the continued fraction here above. Later we explore how this variable influences the final result.

Invoke yambo to run the calculation:

$ yambo -F 03_3D_BSE_haydock_solver.in -J "3D_BSE-low,3D_BSE"  

This outputs the following log:

...
<01s> [06] BSE solver(s)
<01s> [06.01] Haydock solver
<01s> [Haydock] Iteration 1
<03s> [Haydock] Iteration 21 Accuracy :  0.01647| -0.02000
...

The Lanczos-Haydock iterative procedure converged to the desired accuracy in 21 iterations.

This runs only produces human readable files. That means that if you changes the input parameters (such as the broadening or the energy range) the Lanczos-Haydock procedure has to be repeated. Among the human readable files, o-3D_BSE-low.eps_q1_haydock_bse contains the real and imaginary part of the macroscopic dielectric function:

$ less o-3D_BSE-low.eps_q1_haydock_bse
...
#
#  E/ev[1]    EPS-Im[2]  EPS-Re[3]  EPSo-Im[4] EPSo-Re[5] EPS`-Im[6] EPS`-Re[7]
#
   2.00000    0.16089    5.81293    0.04945    4.12727    0.16089    5.81293
   2.03015    0.16711    5.86203    0.05076    4.14234    0.16711    5.86203
...

This file has a slightly different data structure with respect to the diagonalization solver:

Energy in eV | Imaginary part BSE | Real part BSE |Imaginary part IPA | Real part IPA |Imaginary part BSE (it-1) | Real part BSE (it-1)|

We can plot the second and sixth columns and compare with the result from diagonalization:

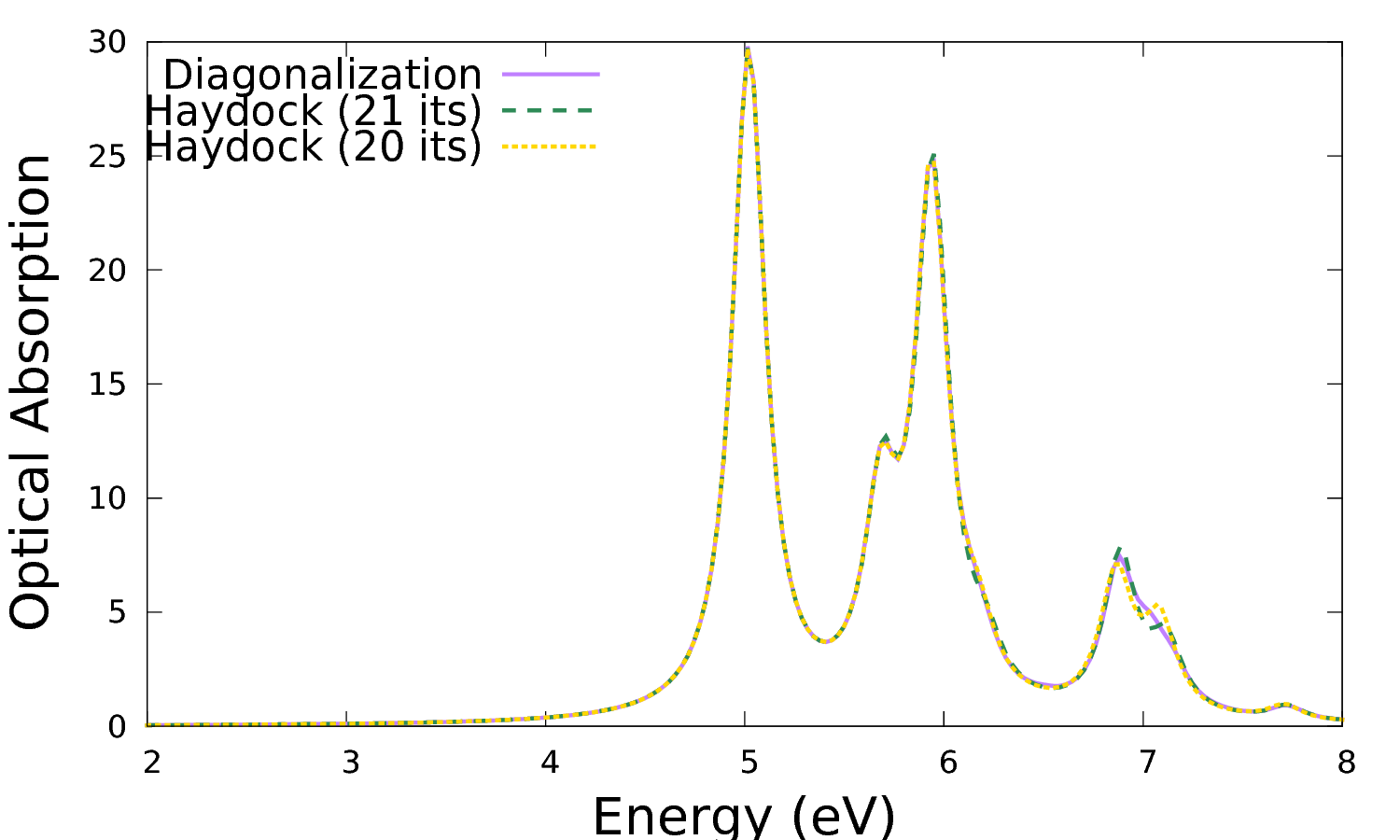
$gnuplot
...
 plot 'o-3D_BSE.eps_q1_diago_bse' u 1:2 w l t 'Diagonalization', 'o-3D_BSE-low.eps_q1_haydock_bse' u 1:2 w l t 'Haydock (27 its)', 'o-3D_BSE-low.eps_q1_haydock_bse' u 1:6 w l t 'Haydock (26 its)'

Except for the peak at higher energy, the results on this scale are identical to those obtained via the diagonalization solver. By comparing the results for the Lanczos-Haydock solver at 27 and 26 iterations, it is clear that the difference with the diagonalization results can be eliminated by lowering the threshold for the iterative process.

Repeat now the calculation by changing the input variable:

BSHayTrs= 0.02000          

which enforces a stricter condition on the convergence of the iterative process (see above)

Running yambo:

$ yambo -F 03_3D_BSE_haydock_solver.in -J "3D_BSE-high,3D_BSE"  

outputs the following log

...
<01s> [06] BSE solver(s)
<01s> [06.01] Haydock solver
<01s> [Haydock] Iteration 1
<06s> [Haydock] Iteration 45 Accuracy :   0.0098|  0.02000
...

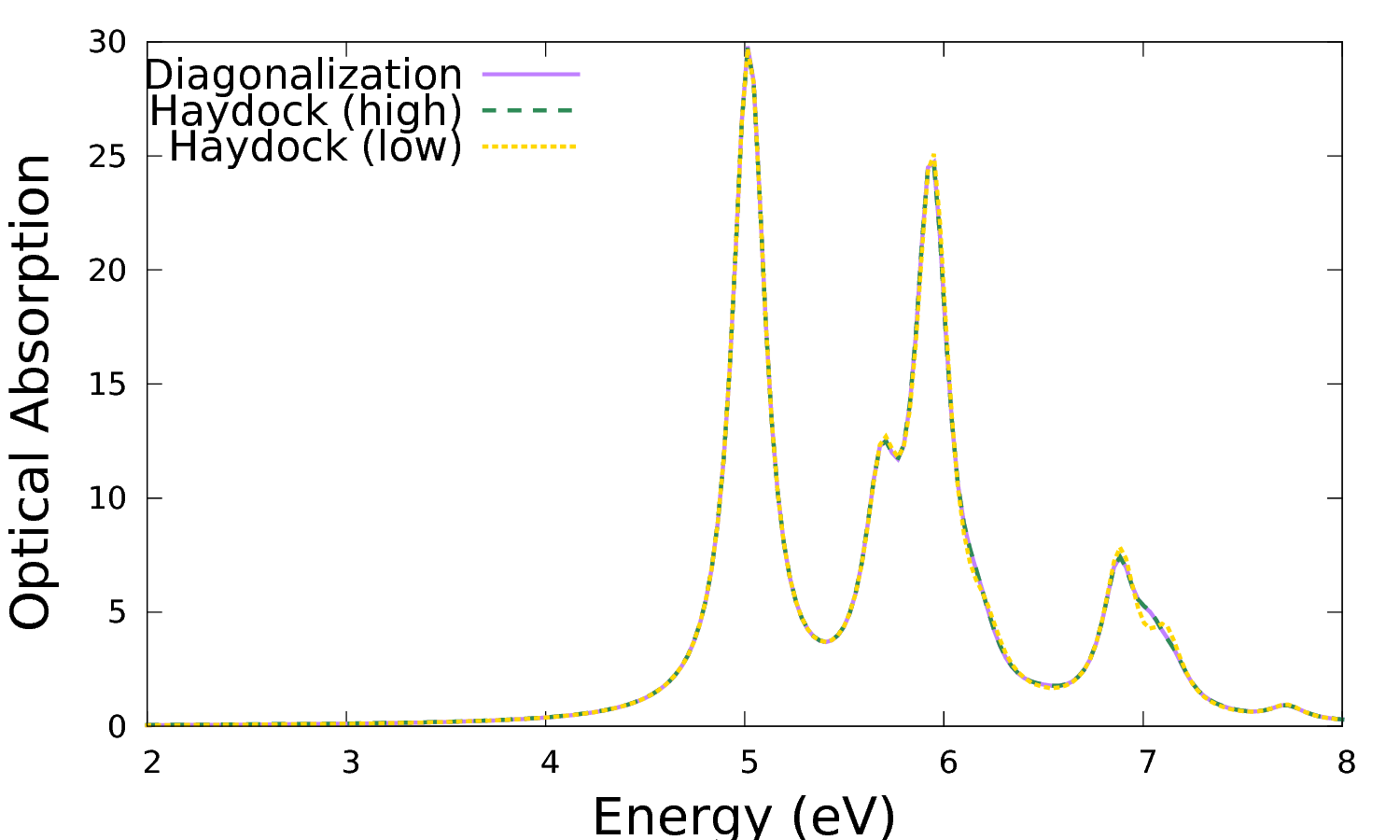
Now 45 iterations, rather than 21, were needed to reach the desired accuracy. By plotting these results:

$ gnuplot
plot 'o-3D_BSE.eps_q1_diago_bse' u 1:2 w l ls 1 t 'Diagonalization', 'o-3D_BSE-high.eps_q1_haydock_bse' u 1:2 w l ls 2 t 'Haydock (high)', 'o-3D_BSE-low.eps_q1_haydock_bse' u 1:2 w l ls 3 t 'Haydock (low)'

Which shows that the Lanczos-Haydock solver with the stricter convergence criterion and the diagonalization solver are identical on this scale.