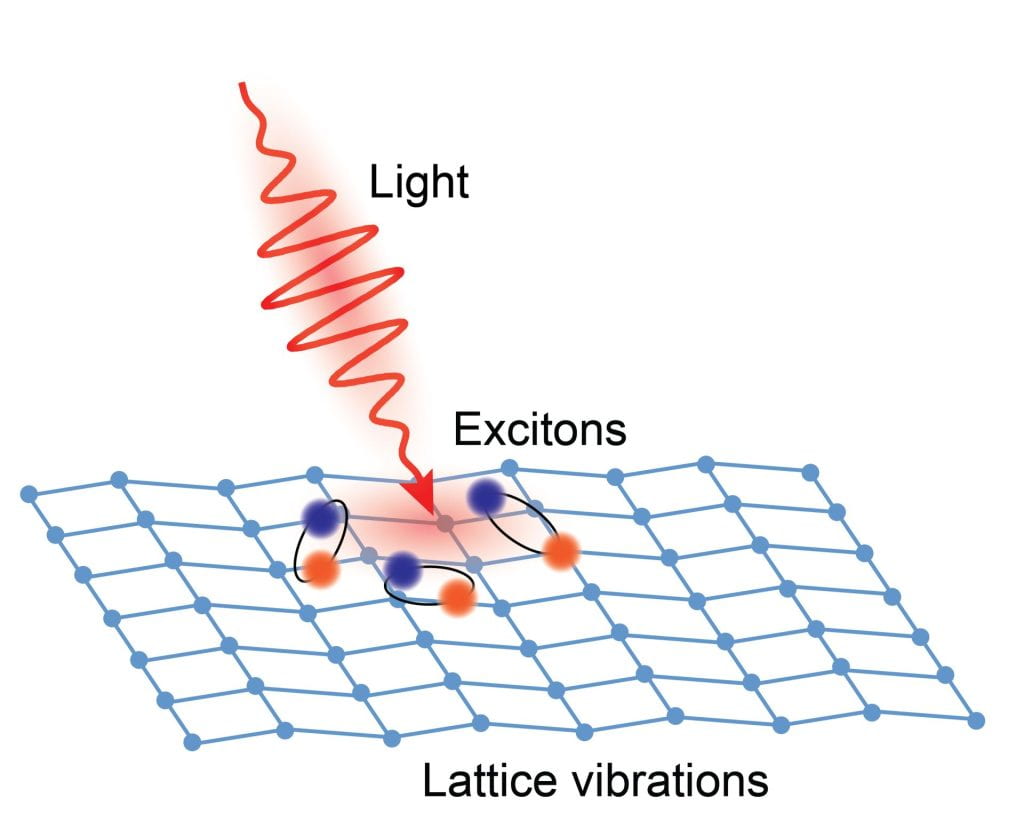
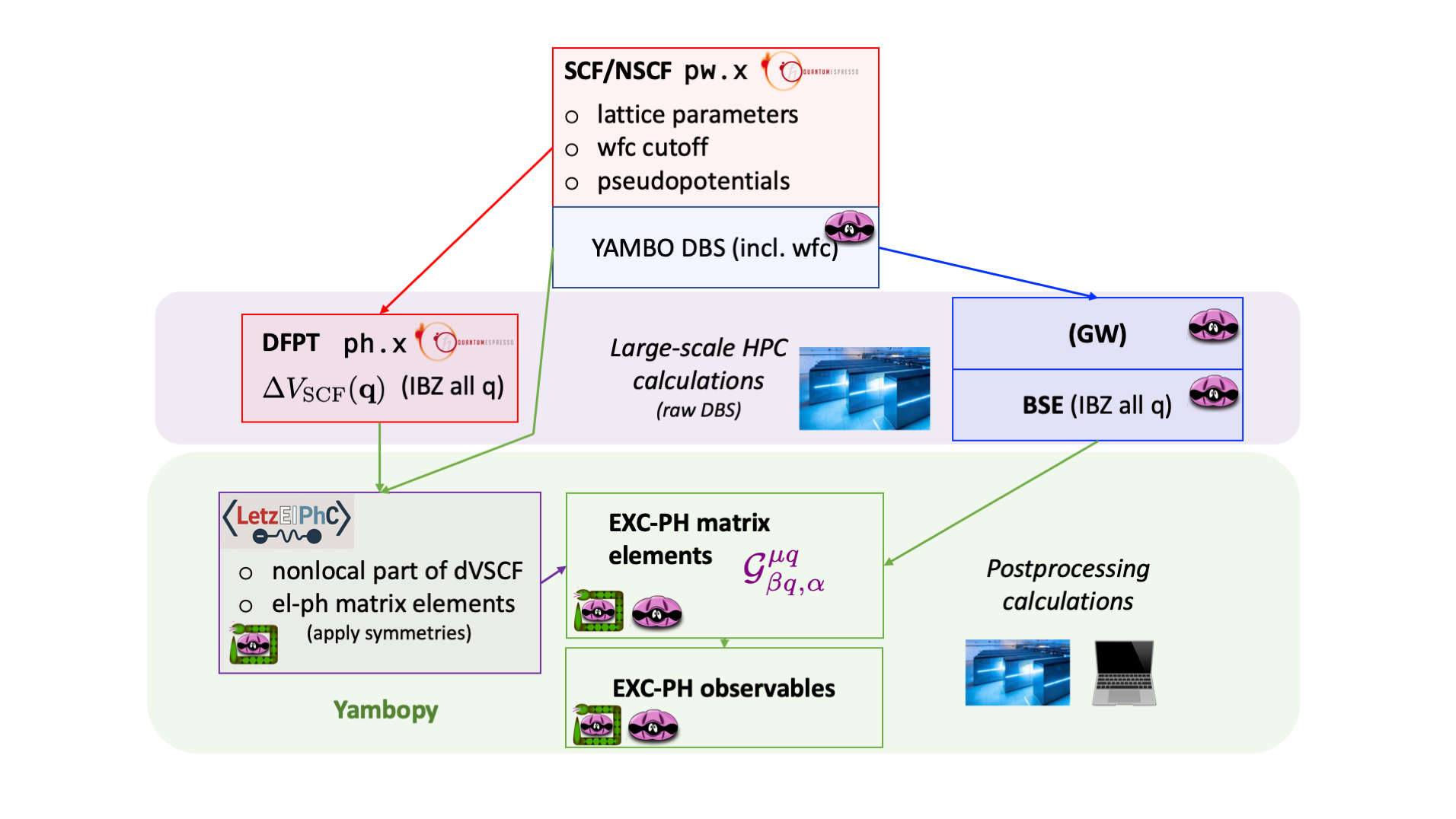
Exciton-phonon coupling and luminescence

In this advanced tutorial, we will calculate exciton-phonon interactions from first principles by interfacing DFPT (for phonon calculations) and BSE (for exciton calculations).

The DFTP calculations are run with Quantum ESPRESSO, while the many-body GW-BSE calculations are run with Yambo. Finally, the exciton-phonon interaction will be obtained by combining and postprocessing the databases computed in the two previous runs. The great advantage of this workflow is that the calculations can be run in the irreducible Brillouin zones both for the electronic momenta ([math]\displaystyle{ k }[/math]) and the transfer momenta ([math]\displaystyle{ Q }[/math], [math]\displaystyle{ q }[/math]) of excitons and phonons, thus speeding up considerably the jobs while reducing the IO and memory load.

We will first compute the exciton-phonon coupling matrix elements: these are the building blocks needed to construct experimental observables such as phonon-assisted optical spectra (such as luminescence), Raman spectra and exciton lifetimes. We will do this in the case of monolayer MoS2, a 2D system with large spin-orbit interaction.

As an example of application, we will consider the case of phonon-assisted luminescence. We will do this in the case of bulk hBN, a layered indirect insulator with strong electron-phonon coupling.

Note: this tutorial will be updated when new exc-ph tools become available in Yambopy (including full-python postprocessing, Raman spectra, interpolated lifetimes, etc).

Requirements

This is an advanced topic: we assume that you already know something about the theory and applications of exciton-phonon physics.

Also, we assume that you already know how to run both a basic Yambo GW-BSE calculation and a DFPT phonon calculation with Quantum ESPRESSO.

Besides the QE executables pw.x and ph.x, we also use the yambo phonon-specific executable yambo_ph and the python utility Yambopy. The auxiliary code LetzElPhC (executable lelphc) will be used to obtain the electron-phonon matrix elements by reading the same electronic wavefunctions used by Yambo (and stored in the SAVE directory), while also making full use of crystal symmetries. LetzElPhC (link) will be run by Yambopy, but it must nonetheless be installed. Finally, the exciton-phonon properties can be computed either using yambo_ph or using Yambopy itself.

Step 0: Pseudopotentials, equilibrium structure and convergence

In a real calculation, it is important to ensure that both the pseudopotential and the lattice parameters that we are using are compatible and perform well for the electronic excited states and for the lattice vibrations simultaneously. Furthermore, you have to make sure that the wave function cutoff ecutwfc is converged with respect to the DFPT step and not just to the DFT one. This is in addition to the other customary convergence tests for DFT, DFPT, GW and BSE calculations.

This is often the most time-demanding step when starting on a new system.

For the sake of this tutorial, we assume that we have already done all these tests and we are starting the final workflow to get the exciton-phonon properties.

Step 1: scf calculation

First of all, we run a standard scf calculation with pw.x for Yambo. We stick with non-symmorphic symmetries. At the end, we will have the QE save directory.

This is the input:

&control
          wf_collect = .true.,
         calculation = "scf",
           verbosity = 'high',
          pseudo_dir = '$PSEUDO_DIR',
              prefix = "mos2",
              outdir = '.',
 /&end
 &system
             ecutwfc = 100.0,
         occupations = 'fixed',
               ibrav = 4,
           celldm(1) = 5.9000811881,
           celldm(3) = 6.7795677253,
                 nat = 3,
                ntyp = 2,
            lspinorb = .true.
            noncolin = .true.
            assume_isolated = '2D'
        force_symmorphic = .true.
 /&end
 &electrons
    electron_maxstep = 200,
         mixing_beta = 0.7,
            conv_thr = 1.d-08,
 /&end
  ATOMIC_SPECIES
   Mo  95.940      Mo_ONCV_PBE_FR-1.0.upf
   S    32.065     S_ONCV_PBE_FR-1.1.upf
  ATOMIC_POSITIONS { crystal }
Mo       0.333333333   0.666666667   0.000000000
S        0.666666667   0.333333333   0.073413577
S        0.666666667   0.333333333  -0.073413577
 K_POINTS { automatic }
6 6 1 0 0 0

Here we are using full relativistic pseudopotentials from the SG-15 database.

We can run it on our machine (for example using 4 MPI tasks) as:

mpirun -np 4 pw.x -inp mos2.scf > scf.out

Step 2: nscf calculation for Yambo

Copy the QE save directory from the scf calculation and run the nscf calculation for any number of empty states, with the correct k-grid we want to use in Yambo. Here we are using a badly underconverged grid of 6x6x1.

This reciprocal-space grid will also match the momentum transfer q grid on which excitons and phonons will be defined!

The electronic wavefunctions computed at this step and stored in the new nscf save directory will be used both by Yambo and by the electron-phonon code: this is important because using different sets of wavefunctions would lead to a phase mismatch issue in the exciton-phonon matrix elements.

The nscf input is

&control
          wf_collect = .true.,
         calculation = "nscf",
           verbosity = 'high',
          pseudo_dir = '$PSEUDO_DIR',
              prefix = "mos2",
              outdir = '.',
 /&end
 &system
             ecutwfc = 100.0,
         occupations = 'fixed',
               ibrav = 4,
           celldm(1) = 5.9000811881,
           celldm(3) = 6.7795677253,
                 nat = 3,
                ntyp = 2,
            lspinorb = .true.
            noncolin = .true.
               nbnd  = 250
            assume_isolated = '2D'
        force_symmorphic = .true.
 /&end
 &electrons
    electron_maxstep = 200,
         mixing_beta = 0.7,
            conv_thr = 1.d-08,
 /&end
  ATOMIC_SPECIES
   Mo  95.940      Mo_ONCV_PBE_FR-1.0.upf
   S    32.065     S_ONCV_PBE_FR-1.1.upf
  ATOMIC_POSITIONS { crystal }
Mo       0.333333333   0.666666667   0.000000000
S        0.666666667   0.333333333   0.073413577
S        0.666666667   0.333333333  -0.073413577
 K_POINTS { automatic }
6 6 1 0 0 0

Again, we run the calculation

mpirun -np 4 pw.x -inp mos2.nscf > nscf.out

Step 3: dvscf phonon calculation

Now we run the phonon calculation.

Copy the save directory from the scf calculation and run ph.x for a dvscf calculation with a standard q-grid matching the k-grid we wanna use in Yambo.

At the end, we will have the _ph0 directory containing the variation of the self-consistent potential, [math]\displaystyle{ \Delta V_{SCF}(q) }[/math], and the *.dyn files with the phonon energies and eigenvectors.

NB: one could further refine the phonon energies by enforcing the acoustic sum rule, including non-analytic long-range contributions, interpolating to finer grids... all of this can be done within Quantum ESPRESSO and will not be covered in this version of the tutorial.

The input is

mos2_dvscf
&inputph
  tr2_ph=1.0d-12,
  verbosity='high'
  prefix='mos2',
  fildvscf = 'mos2-dvscf',
  electron_phonon = 'dvscf',
  fildyn='mos2.dyn',
  epsil=.false.,
  ldisp=.true.,
  recover=.true.,
  nq1=6,
  nq2=6,
  nq3=1
/

And now we run as

nohup mpirun -np 8 ph.x -inp mos2.dvscf > dvscf.out &

This time we use nohup and more processes because this calculation may take some time. It is a good idea to set recover=.true. as in a real calculation you will easily breach walltime, and in this way you can safely restart.

Step 4: Step 4: create Yambo SAVE directory

This is just the standard Yambo initialization: run

p2y 

and then

yambo 

in the nscf save folder and then move the newly generated SAVE directory to a convenient place.

Step 5: run a BSE calculation

Now we switch from QE to Yambo. Here, we forgo the GW step for simplicity (we can use a scissor operator to open the band gap).

This calculation has a couple of differences with respect to a standard BSE calculation for optical absorption. We can look at the input file:

# Runlevels
optics                       # [R OPT] Optics
rim_cut                      # [R RIM CUT] Coulomb potential
bss                          # [R BSS] Bethe Salpeter Equation solver
em1s                         # [R Xs] Static Inverse Dielectric Matrix
bse                          # [R BSE] Bethe Salpeter Equation.
bsk                          # [R BSK] Bethe Salpeter Equation kernel
# RIM and cutoff settings
RandQpts=1000000             # [RIM] Number of random q-points in the BZ
RandGvec= 100            RL    # [RIM] Coulomb interaction RS components
CUTGeo= "slab z"               # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY..
# Static screening
X_and_IO_CPU= "1 1 4 2 1"       # [PARALLEL] CPUs for each role
X_and_IO_ROLEs= "q g k c v"      # [PARALLEL] CPUs roles (q,g,k,c,v)
X_and_IO_nCPU_LinAlg_INV=-1      # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set)
Chimod= "hartree"            # [X] IP/Hartree/ALDA/LRC/BSfxc
% QpntsRXs
   1 | 7 |                 # [Xs] Transferred momenta
%
% BndsRnXs
   1 |  200 |                 # [Xs] Polarization function bands
%
% LongDrXs
 1.000000 | 1.000000 | 1.000000 |        # [Xs] [cc] Electric Field
%
NGsBlkXs= 8            Ry    # [Xs] Response block size
# BSE
BS_CPU= "4.1.2"                   # [PARALLEL] CPUs for each role
BS_ROLEs= "k.eh.t"                 # [PARALLEL] CPUs roles (k,eh,t)
BS_nCPU_diago=4              # [PARALLEL] CPUs for matrix diagonalization
BSEmod= "causal"             # [BSE] resonant/causal/coupling
BSKmod= "SEX"                # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
BSSmod= "d"                  # [BSS] (h)aydock/(d)iagonalization/(i)nversion/(t)ddft`
BSENGexx=  40          Ry    # [BSK] Exchange components
ALLGexx                      # [BSS] Force the use use all RL vectors for the exchange part
BSENGBlk=  8           Ry    # [BSK] Screened interaction block size
Lkind="full"                  #[BSE,X] bar(default)/full/tilde
% KfnQP_E
 1.000000 | 1.000000 | 1.000000 |        # [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim
%
% BEnRange
  0.00000 |  4.00000 | eV    # [BSS] Energy range
%
% BDmRange
  0.05000 |  0.05000 | eV    # [BSS] Damping range
%
BEnSteps= 2000               # [BSS] Energy steps
% BLongDir
 1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
%
% BSEQptR
 1 | 7 |                     # [BSK] Transferred momenta range
%
% BSEBands
   25 |  28 |                 # [BSK] Bands range
%
WRbsWF                      # [BSS] Write to disk excitonic the FWs

First of all, we compute the excitons for all the momenta in our discrete grid via the BSEQptR variable. This will be a finite-momentum BSE calculation, analogous to the phonon one.

Second, we change the variable Lkind from bar to full. In Yambo, Lkind="bar", which is the default for optical absorption, means that we are computing the excitonic response function without the long-range component of the exchange interaction. This cannot be used when computing the exciton momentum dependence, where the long-range exchange interaction can play a role, therefore we have to include it with Lkind="full". This allows for the calculation of the excitonic longitudinal-transverse splitting (in 3D systems) as well.

We can now run the code:

nohup mpirun -np 8 yambo -F bse.in -J bse_Lfull -C bse_Lfull &

At the end of the calculation, we have obtained the ndb.BS_diago_Q* databases inside the directory bse_Lfull. They contain information on the exciton energies and wavefunctions at each momentum. Do not forget to check the report and logs of your calculation in the same directory to make sure that the code is doing what you want.