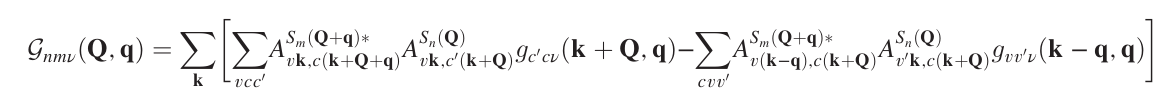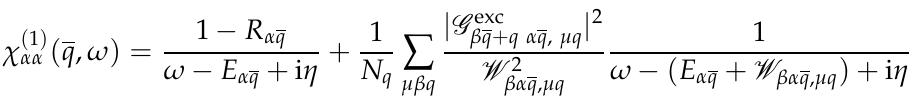Exciton-phonon coupling and luminescence
This an advanced tutorial, in order to calculate exciton-phonon coupling[1] and phonon-assisted absorption/emission you need a deep knowledge of the theory and of the Yambo code.
In this tutorial we will calculate phonon-assisted absorption and luminescence including the scattering between exciton and phonon.[2][3][4]
We will consider as example bulk hBN. Notice that parameters of the present tutorial are not at convergence, but are just as a possible example.
The tutorial includes several steps and the calculations can be quite expensive.
Getting the code
This tutorial works only with Yambo version > 6.x, but a preliminary version of the code is available on github:
https://github.com/attacc/yambo-excph
Notice that this version is for testing purpose only, it's not fully tested therefore we advice you do not use it in production. In order to install yambo with exciton-phonon coupling you do:
git clone git@github.com:attacc/yambo-excph.git cd yambo-excph ./configure make core make ph-project
Electron-phonon matrix elements
Here you will find a script and all input files to run the a small example on hBN
In the tgz file you will find a script run_dvscf.sh a python script and different folders with the QE input files. You have to modify run_dvscf.sh in order to set the correct path of Yambo and QuantumEspresso on your PC, the number of processors to use, and the parallelization command. Then run:
./run_dvscf.sh
it will generate electron-phonon coupling on a Q-grid 12x12x1 for bulk hBN. Generation of electron-phonon matrix elements can take time, one my PC (core i9) it takes 1 hour with 8 cores, you can decrease the number of k-point to 8x8 to speed up calculations. The script will perform self-consistent calculation for the density, then non-self-consistent for the band structure, calculation of phonons on a special q-grid and finally the calculation of electron-phonon matrix elements. All these data, wave-functions, and electron-phonon matrix elements are then transformed in the Yambo format.
You can go in the QPT12/dvscf/bn.save folder and start calculation from here.
BSE at finite momentum
Run the BSE for all momentum q as explained in the tutorials: BSE basic, BSE convergence, BSE for 2D.
Do not forget to turn on the flag WRbsWF to write the excitonic wave-functions.
You can generate the input for the BSE with the command: yambo_ph -X s -o b -y d -V qp -k sex
em1s # [R][Xs] Statically Screened Interaction optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. dipoles # [R] Oscillator strenghts (or dipoles) BoseTemp=-1.000000 eV # Bosonic Temperature DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 14923 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] #WehCpl # [BSK] eh interaction included also in coupling KfnQPdb= "none" # [EXTQP BSK BSS] Database action KfnQP_INTERP_NN= 1 # [EXTQP BSK BSS] Interpolation neighbours (NN mode) KfnQP_INTERP_shells= 20.00000 # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode) KfnQP_DbGd_INTERP_mode= "NN" # [EXTQP BSK BSS] Interpolation DbGd mode % KfnQP_E 3.000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % % BSEQptR 1 | 19 | # [BSK] Transferred momenta range % % BSEBands 7 | 10 | # [BSK] Bands range % % BEnRange 0.00000 | 10.00000 | eV # [BSS] Energy range % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 300 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane WRbsWF # [BSS] Write to disk excitonic the WFs % BndsRnXs 1 | 16 | # [Xs] Polarization function bands % NGsBlkXs= 51 RL # [Xs] Response block size % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field %
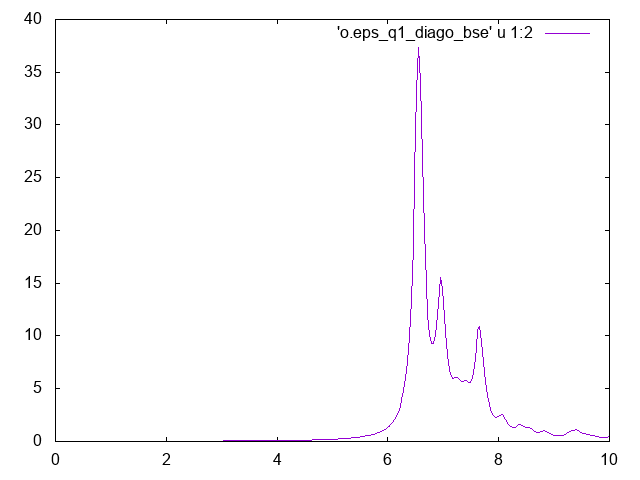
In the BSE we included only the two top valence bands 7,8 and the bottom conduction bands 9,10, a scissor of 3.0 eV, and the dielectric constant used to calculate W include 16 bands and a block size of 51 plane waves. Notice that we calculate the BSE for all the 19 possible transfer momentum. In this input file we used the full diagonalization BSSmod= "d" , for large system it is better to switch to the Slepc libraries '-y s' in the input file generation. If you plot the optical spectra, the file o.eps_q1_diago_bse you should get something like this:
Exciton-phonon matrix elements and optics
Now that you have the BSE for all momentum and the gkkp_expanded databases you can create the exciton-phonon matrix elements, according to the equation:
and calculate optical response as:
where Wβα,μq =Eβq − Eα + ωqμ ,for more details see Ref.[5]. Phonon-assisted optical response and exciton-phonon matrix elements can be calculated with the command: yambo_ph -excph o
excph # [R] Exction-phonon ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements ExcPhOptics # [R][EXCPH] Exciton-Phonon Optics BoseTemp=1.000000 K # Bosonic Temperature % ELPhExcStates 1 | 2 | # [EXCPH] Incoming (external) exciton states % % ELPhExcSum 1 | 8 | # [EXCPH] Outgoing (virtual) exciton states % LoutPath= "none" # [EXCPH] Path of the outgoing L % ElPhModes 1 | 4 | # [ELPH] Phonon modes included % EXCTemp= 50.000000 Kn # [EXCPH] Excitonic Temperature (for luminescence spectra) #DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements #DbGdWEIGHTs # [EXCPH] Use Double-grid also for satellite weights and re-normalization % EnRngeXd 5.00000 | 10.00000 | eV # [Xd] Energy range % % DmRngeXd 0.02500000 | 0.02500000 | eV # [Xd] Damping range % ETStpsXd= 500 # [Xd] Total Energy steps
where the ELPhExcStates state are the one responsible for the absorption and emission, the α indexes in the χαα and ELPhExcSum are the virtual exciton states that enter in the exciton-phonon scattering, namely the β index in the sum χαα. Running the code, Yambo calculates all the exciton-phonon matrix elements and the photon assisted absorption and emission spectra. The emission spectra is calculated using the Roosbroeck–Shockley (RS) relation[6], a Boltzman distribution for the excitonic occupation at temperature EXCTemp, for more detail see Refs.[5][3], other ways for excitonic occupations are possible, for a discussion see Ref.[2].
LoutPath is the path of the outgoing Bethe-Salpeter, in principle one can use two different kind of exciton for virtual and real exciton in above equation. If LoutPath='none' Yambo will read excitons in the same folder of the incoming ones, by default the SAVE folder.
If the flag DbGdWEIGHTs is turned one the Double-Grid is used also for the denominators in the satellite weights and for the rernomalization factors (default FALSE).
Exciton lifetimes
Using the exciton-phonon coupling it is possible also to calculate exciton life-time due to the scattering with phonon. The command yambo -excph l will generate the corresponding input:
excph # [R] Exction-phonon
ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements
ExcPhLifeT # [R][EXCPH] Exciton-Phonon Life-Times
BoseTemp= 1.000000 eV # Bosonic Temperature
EXCTemp= 0.000000 eV # [EXCPH] Excitonic Temperature (for luminescence spectra)
% ELPhExcStates
1 | 4 | # [EXCPH] Incoming (external) exciton states
%
% ELPhExcSum
1 | 8 | # [EXCPH] Outgoing (virtual) exciton states
%
% ElPhModes
1 | 6 | # [ELPH] Phonon modes included
%
LoutPath= "none" # [EXCPH] Path of the outgoing L
#DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements
LDamping= 0.5 meV # [EXCPH] Damping of exc-ph self-energy
notice that in this case LDamping is the broadening of the exciton-phonon self energy and it should be a very small value of the order of the phonon life-times about 0.5 meV.[7]
Convergence and double-grid
The exciton-phononn coupling code is compatible with the Double-Grid approach. You can generate a double grid for the phonon energies as explained in Double-grid method for the electron-phonon coupling and then the excitonic energies are interpolated using a smooth Fourier interpolation, see Ref.[8]. The best strategy to converge the spectra it is to chose a grid for the exciton-phonon matrix elements and then converge the double-grid, then repeat the calculation with a large exciton-phonon coupling grid and so on... similar to the electron-phonon case.
References
- ↑ Optical processes in solids, Toyozawa, Yutaka, and Chris Oxlade. Cambridge University Press, (2003).
- ↑ 2.0 2.1 Theory of phonon-assisted luminescence in solids: Application to hexagonal boron nitride, E. Cannuccia, B. Monserrat and C. Attaccalite, Phys. Rev. B 99, 081109(R) (2019)
- ↑ 3.0 3.1 Exciton-Phonon Coupling in the Ultraviolet Absorption and Emission Spectra of Bulk Hexagonal Boron Nitride, F. Paleari et al. PRL 122, 187401(2019)
- ↑ Exciton-Phonon Interaction and Relaxation Times from First Principles, Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, Phys. Rev. Lett. 125, 107401(2020)
- ↑ 5.0 5.1 First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride, F. Paleari PhD thesis
- ↑ Photon-Radiative Recombination of Electrons and Holes in Germanium, W. van Roosbroeck and W. Shockley, Phys. Rev. 94, 1558 (1954)
- ↑ First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong an-harmonicity: The example of palladium hydrides, L. Paulatto, et al. Phys. Rev. B 91, 054304 (2015)
- ↑ Smooth Fourier interpolation of periodic functions, Warren E. Pickett, Henry Krakauer, and Philip B. Allen, Phys. Rev. B 38, 2721(1988)