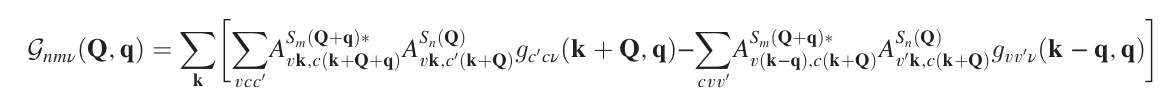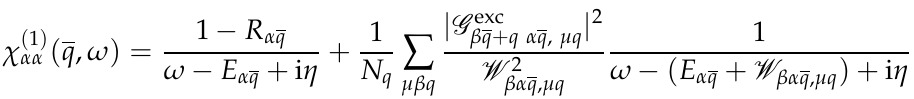Exciton-phonon coupling and luminescence
This tutorial works only with Yambo version > 6.x
A preliminary version of Yambo with exciton-phonon coupling is available here:
This tutorial is for internal use of the Yambo developers, Yambo 6.0 will not be available until 2024
This an advanced tutorial, in order to calculate exciton-phonon coupling[1] and phonon-assisted absorption/emission you need a deep knowledge of the theory and of the Yambo code.
In this tutorial we will calculate phonon-assisted absorption and luminescence including the scattering between exciton and phonon.[2][3][4]
We will consider as example bulk silicon. Notice that parameters of the present tutorial are not at convergence, but are just as a possible example.
The tutorial includes several steps and the calculations can be quite expensive.
Electron-phonon matrix elements
First of all we calculate electron-phonon matrix elements as explained in the section: Electron-phonon matrix elements but in the last passage of the tutorial we expand the electron-phonon matrix elements in all the Brillouin Zone. In order to do so, when we read the electron-phonon matrix elements from QE with the command ypp_ph -g g we turn on the flag GkkpExpand
gkkp # [R] gkkp databases gkkp_db # [R] GKKP database #GkkpReadBare # Read the bare gkkp DBsPATH= "../elph_dir/" # Path to the PW el-ph databases PHfreqF= "none" # PWscf format file containing the phonon frequencies PHmodeF= "none" # PWscf format file containing the phonon modes GkkpExpand # Expand the gkkp in the whole BZ #UseQindxB # Use qindx_B to expand gkkp (for testing purposes)
if everything worked fine in the log you will find:
.... <---> :: Uniform sampling :yes <---> :: Symmetry expanded :yes .....
Notice that in the calculation of the electron-phononn coupling you need a number of conduction bands as large as the one that will be used in the Bethe-Salpeter Equation.
Remove all symmetries
Now we remove all symmetries with the command ypp_ph -y
fixsyms # [R] Remove symmetries not consistent with an external perturbation
% Efield1
0.000000 | 0.000000 | 0.000000 | # First external Electric Field
%
% Efield2
0.000000 | 0.000000 | 0.000000 | # Additional external Electric Field
%
BField= 0.000000 T # [MAG] Magnetic field modulus
Bpsi= 0.000000 deg # [MAG] Magnetic field psi angle [degree]
Btheta= 0.000000 deg # [MAG] Magnetic field theta angle [degree]
RmAllSymm # Remove all symmetries
#RmTimeRev # Remove Time Reversal
#RmSpaceInv # Remove Spatial Inversion
#KeepKGrid # Do not expand the k-grid
the code will expand the electronic wave-function and copy the gkkp_expanded databases in the new folder.
BSE at finite momentum
Run the BSE for all momentum q as explained in the tutorials: BSE basic, BSE convergence, BSE for 2D.
Do not forget to turn on the flag WRbsWF to write the excitonic wave-functions.
Exciton-phonon matrix elements and optics
Now that you have the BSE for all momentum and the gkkp_expanded databases you can create the exciton-phonon matrix elements, according to the equation:
and calculate optical response as:
where Wβα,μq =Eβq − Eα + ωqμ ,for more details see Ref.[5]. Phonon-assisted optical response and exciton-phonon matrix elements can be calculated with the command: yambo_ph -excph o
excph # [R] Exction-phonon ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements ExcPhOptics # [R][EXCPH] Exciton-Phonon Optics BoseTemp=1.000000 K # Bosonic Temperature % ELPhExcStates 1 | 2 | # [EXCPH] Incoming (external) exciton states % % ELPhExcSum 1 | 8 | # [EXCPH] Outgoing (virtual) exciton states % LoutPath= "none" # [EXCPH] Path of the outgoing L % ElPhModes 1 | 6 | # [ELPH] Phonon modes included % EXCTemp= 0.000000 eV # [EXCPH] Excitonic Temperature (for luminescence spectra) #DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements #DbGdWEIGHTs # [EXCPH] Use Double-grid also for satellite weights and re-normalization % EnRngeXd 0.00000 | 10.00000 | eV # [Xd] Energy range % % DmRngeXd 0.100000 | 0.100000 | eV # [Xd] Damping range % ETStpsXd= 100 # [Xd] Total Energy steps
where the ELPhExcStates state are the one responsible for the absorption and emission, the α indexes in the χαα and ELPhExcSum are the virtual exciton states that enter in the exciton-phonon scattering, namely the β index in the sum χαα. Running the code, Yambo calculates all the exciton-phonon matrix elements and the photon assisted absorption and emission spectra. The emission spectra is calculated using the Roosbroeck–Shockley (RS) relation[6], a Boltzman distribution for the excitonic occupation at temperature EXCTemp, for more detail see Refs.[5][3], other ways for excitonic occupations are possible, for a discussion see Ref.[2].
LoutPath is the path of the outgoing Bethe-Salpeter, in principle one can use two different kind of exciton for virtual and real exciton in above equation. If LoutPath='none' Yambo will read excitons in the same folder of the incoming ones, by default the SAVE folder.
If the flag DbGdWEIGHTs is turned one the Double-Grid is used also for the denominators in the satellite weights and for the rernomalization factors (default FALSE).
Exciton lifetimes
Using the exciton-phonon coupling it is possible also to calculate exciton life-time due to the scattering with phonon. The command yambo -excph l will generate the corresponding input:
excph # [R] Exction-phonon
ExcGkkp # [R][EXCPH] Exciton-Phonon Matrix Elelements
ExcPhLifeT # [R][EXCPH] Exciton-Phonon Life-Times
BoseTemp= 1.000000 eV # Bosonic Temperature
EXCTemp= 0.000000 eV # [EXCPH] Excitonic Temperature (for luminescence spectra)
% ELPhExcStates
1 | 4 | # [EXCPH] Incoming (external) exciton states
%
% ELPhExcSum
1 | 8 | # [EXCPH] Outgoing (virtual) exciton states
%
% ElPhModes
1 | 6 | # [ELPH] Phonon modes included
%
LoutPath= "none" # [EXCPH] Path of the outgoing L
#DiagExcph # [EXCPH] Use only Diagonal Exciton-phonon matrix elements
LDamping= 0.5 meV # [EXCPH] Damping of exc-ph self-energy
notice that in this case LDamping is the broadening of the exciton-phonon self energy and it should be a very small value of the order of the phonon life-times about 0.5 meV.[7]
Convergence and double-grid
The exciton-phononn coupling code is compatible with the Double-Grid approach. You can generate a double grid for the phonon energies as explained in Double-grid method for the electron-phonon coupling and then the excitonic energies are interpolated using a smooth Fourier interpolation, see Ref.[8]. The best strategy to converge the spectra it is to chose a grid for the exciton-phonon matrix elements and then converge the double-grid, then repeat the calculation with a large exciton-phonon coupling grid and so on... similar to the electron-phonon case.
References
- ↑ Optical processes in solids, Toyozawa, Yutaka, and Chris Oxlade. Cambridge University Press, (2003).
- ↑ 2.0 2.1 Theory of phonon-assisted luminescence in solids: Application to hexagonal boron nitride, E. Cannuccia, B. Monserrat and C. Attaccalite, Phys. Rev. B 99, 081109(R) (2019)
- ↑ 3.0 3.1 Exciton-Phonon Coupling in the Ultraviolet Absorption and Emission Spectra of Bulk Hexagonal Boron Nitride, F. Paleari et al. PRL 122, 187401(2019)
- ↑ Exciton-Phonon Interaction and Relaxation Times from First Principles, Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, Phys. Rev. Lett. 125, 107401(2020)
- ↑ 5.0 5.1 First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride, F. Paleari PhD thesis
- ↑ Photon-Radiative Recombination of Electrons and Holes in Germanium, W. van Roosbroeck and W. Shockley, Phys. Rev. 94, 1558 (1954)
- ↑ First-principles calculations of phonon frequencies, lifetimes, and spectral functions from weak to strong an-harmonicity: The example of palladium hydrides, L. Paulatto, et al. Phys. Rev. B 91, 054304 (2015)
- ↑ Smooth Fourier interpolation of periodic functions, Warren E. Pickett, Henry Krakauer, and Philip B. Allen, Phys. Rev. B 38, 2721(1988)