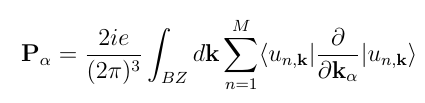Dielectric function from Bloch-states dynamics
Step 0: Theoretical background
The dynamics of Bloch-states is found by integrating a set of Time Dependent Effective Schrödinger Equations (TD-ESEs). Effective means that an effective Hamiltonian is considered. We consider the many-body effective Hamiltonians seen in the Linear response from real time simulations. In addition, one can also consider effective Hamiltonians based on density-functional theory. The latter choice gives time-dependent density-functional theory.
At difference with what seen in Linear response from real time simulations, the coupling between electrons and the external field is described by means of the Modern Theory of Polarization:
Where [math]\displaystyle{ | v_{i \mathbf{k}} \rangle }[/math] are the time-dependent Bloch states (corresponding to the filled Bloch-states at zero-field), [math]\displaystyle{ \mathcal E(t) }[/math] is the external field and the term [math]\displaystyle{ i e \partial k }[/math] is the dipole operator consistent with periodic boundary condition. For more details on this last term, see Ref. [1] and [2].
[math]\displaystyle{ h_{rt} }[/math] is the Hamiltonian,
.
This contains the equilibrium Hamiltonian, that is the zero-field eigenvalues evaluated through DFT; the quasiparticle corrections, evaluated from GW or estimated from experiment, and the variation of the self-energy. The latter is a functional of the density matrix [math]\displaystyle{ \rho }[/math], which is obtained from the Bloch states.
From the solution of the equation of motion for the Bloch states, the polarization is calculated by means of Berry's phase
.
One can decide the level of theory by selecting the terms to include in the Hamiltonian:
- by including only the first term, one selects the independent-particle approximation
- by including the first and second terms, one selects the independent-quasiparticle approximation
- by including the first, second terms and the Hartree part of the self-energy, one selects the time-dependent Hartree or random-phase approximation
- by including all terms, one selects the time-dependent Screened-exchange or Bethe-Salpeter equation level of theory.
The type of "experiment" to perform, or of the response one would like to extract, depend on the time-dependent field in input and the post-processing of the Berry's phase polarization. For example, in the case of linear response, the time-dependent field is a delta-function that excites all frequencies of the system and the response is obtained by taking the Fourier-transform of the polarization.
Notes:
- Length vs Velocity gauge: the equations of motion of Yambo are in the length gauge. Other codes choose instead to work in the velocity gauge. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of Ref. [3].
- Advantages and disadvantages with respect to the density-matrix based formalism: Yambo implements two distinct formalisms for studying the real-time response, the one based on density-matrix and the one based on Boch states. Which formalism is best to use depends on what one wants to simulate. The dynamics formulation in terms of density matrix or non-equilibrium Green's functions allows a systematic treatment of correlation effects and electron-phonon coupling[4], but the price to pay is that the coupling with the external field is correct only to the linear order. This formalism is important in all those phenomena where electronic relaxation plays a major role. On the other hand, the formulation in terms of the Bloch states treats coupling with the external field in an exact way even beyond the linear regime, and for this reason, it allows the description of phenomena coherent with the external fields and to access, for example, non-linear responses.
Step 1: Prerequisites
In this example, we will consider a single layer of hexagonal boron nitride (hBN). Before running real time simulations in yambo you need to:
- download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz.
- perform the steps described in Prerequisites for Real Time propagation with Yambo.
Step 2: Independent-particles approximation
Similar to what you have seen in the tutorial for the density matrix formalism (Real time approach to linear response)
- ↑ I. Souza, J. Íñiguez, and D. Vanderbilt, PRB 69, 085106 (2004)
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)
- ↑ C. Attaccalite, arXiv 1609.09639 (2017)
- ↑ D. Sangalli, and A. Marini EPL 110, 47004 (2015)