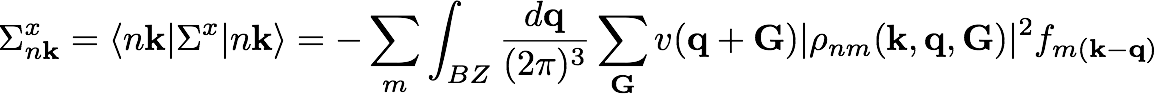Hartree Fock
Prerequisites
- Complete the Generating the Yambo databases tutorial
SAVEfolder for bulk hBN.yamboexecutable- Run Initialization
The exchange part contribution of the self-energy for a generic state (nk) in reciprocal space reads:
It is important to note that in this way we are adding the HF contribution in a perturbative way to previously calculated DFT energies:
and hence they will differ from a standard self-consistent HF calculation.
Let's start by building up the input file for an HF calculation by typing:
$ yambo -x -V all -F hf.in
Looking inside the input file you will find:
EXXRLvcs = 1491 RL # [XX] Exchange RL components %QPkrange # [GW] QP generalized Kpoint/Band indices 1| 14| 1|100| %
The variable EXXRLvcs governs the number of G vector to be summed in the expression of the exchange self-energy reported above. The QPkrange name list it is a generalized index needed to select the first and last kpoints and bands we want to calculate the QP correction. Let's start by editing the hf.in file by considering the last occupied and first empty bands in order to calculate the direct gap, and run calculations to converge the expression above. So we change the QPkrange variable in:
%QPkrange # [GW] QP generalized Kpoint/Band indices 14| 14| 8| 9| %
In the expression of the Exchange Self Energy, we have a summation over bands, an integral over the Brillouin Zone and a Sum over the G vectors. Looking at the occupation factor we realize that occupied states only enters in the expression, so we do not need to worry about the bands as Yambo will include all the occupied bands by default. In order to check convergence of the G vectors in the summation in the Σx expression, we will perform different calculation varying the kinetic energy cutoff governing the number of G vectors entering in the sum. Let's start by setting in hf.in:
EXXRLvcs= 10 Ry
and run yambo:
$ yambo -F hf.in -J 3D
The result can be found int the output o-D3.hf file and in the r-D3_HF_and_locXC file. Looking inside the output file we have:
# # K-point Band Eo Ehf DFT HF # 14.00000 8.00000 0.00000 -2.24181 -16.23328 -18.47509 14.00000 9.00000 4.35241 9.82477 -11.23580 -5.76344 #
Looking at the definition of the HF energy, the third column is the DFT energy (KS eigenvalue), Ehf is the HF energy, and column 4 and 5 report the different contribution to be subtracted Vx (DFT) and added Σx (HF) to the unperturbed DFT eigenvalue.