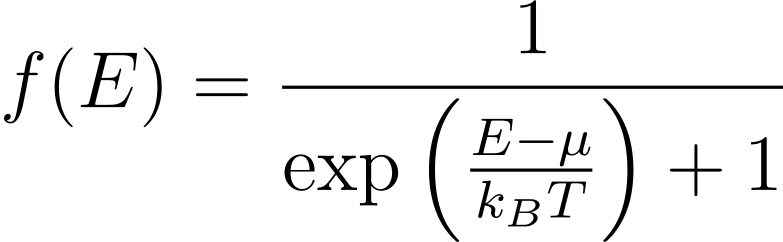Nonequilibrium absorption in bulk silicon: Difference between revisions
Petru Milev (talk | contribs) |
Petru Milev (talk | contribs) |
||
| Line 330: | Line 330: | ||
1 | 40 | # [GW] G[W] bands range | 1 | 40 | # [GW] G[W] bands range | ||
% | % | ||
to force Yambo to do a calculation where self-energy depends on the conduction bands too. Alternatively, an option option <code>-V qp</code> can be added when generating the file, but it will include a lot of redundant variables. | to force Yambo to do a calculation where self-energy depends on the conduction bands too, or this is also known as [https://wiki.yambo-code.eu/wiki/index.php?title=Silicon COHSEX with empty bands]. Alternatively, an option option <code>-V qp</code> can be added when generating the file, but it will include a lot of redundant variables. | ||
And after it we run the file with the following command: | And after it we run the file with the following command: | ||
Revision as of 14:47, 25 November 2024
In this tutorial you will learn the basic concepts for computing changes in the optical properties of a semi-conductor in presence of a non-equilibrium electrons and holes distribution in conduction and valence band respectively. This tutorial is based on the results published in Phys. Rev. B[1]
Under construction
The material: Silicon
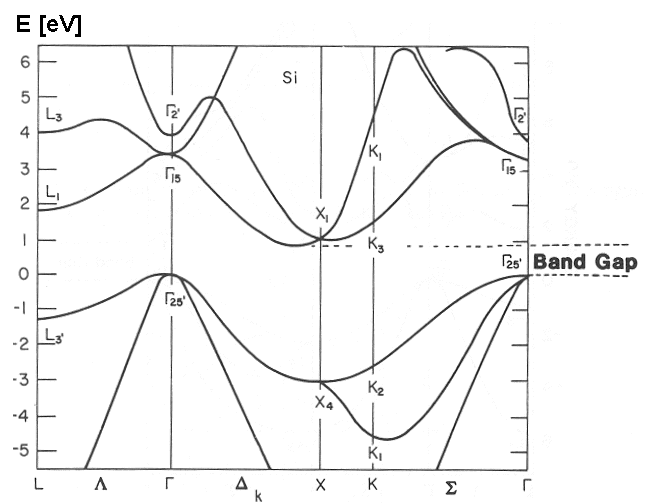
We will study nonequilibrium absorption in bulk silicon. The same material used for this GW tutorial
- FCC lattice
- Two atoms per cell (8 electrons)
- Lattice constant 10.183 [a.u.]
- Plane waves cutoff 15 Rydberg
- Direct gap 3.4 eV at Gamma
- Indirect gap 1.1 eV between Gamma= (0 0 0) and a point X', close to X=(0 1 0)
Tutorial files and Tutorial structure
Follow the instructions in Tutorials#Files and download/unpack the Silicon.tar.gz.
Once the tutorial archive file is unzipped the following folder structure will appear
COPYING README Silicon/
with the Solid_Si folder containing
> ls Silicon/ PWSCF/ YAMBO/
In the Pwscf folder the student will find an input/output directory with input/output files for pw.x. The Silicon pseudopotential file is also provided.
> ls PWSCF/ convergence_scripts input output psps
In the convergence_scripts you will find some useful shell scripts to run the ground state convergence runs for Silicon.
The YAMBO folder contains the Yambo input/output files and core databases.
> ls YAMBO/ 2x2x2/ 4x4x4/ 6x6x6/ 8x8x8/ Convergence_Plots_and_Scripts/ GAMMA/
The core databases are provided for several k-points grids. In addition the folder Convergence_Plots_and_Scripts contains some scripts used for the [Silicon|GW tutorial] .
Here we will just use the 8x8x8 (which is still very far from convergence) folder for computing (nonequilibrium) optical properties.
To run the tutorial you will need the standard executables
yambo ypp
plus the executables of the real time module of the Yambo code
yambo_rt ypp_rt
Overview of the simulations in this tutorial
We start from a density-functional theory (DFT) calculation as the foundation. As a first demonstrative step, we will solve the Bethe-Salpeter equation (BSE) for the equilibrium case without including quasiparticle (QP) corrections. Once this is completed, we will use the Yambo post-processing module, ypp_rt, to generate a distribution of non-equilibrium carriers. This distribution will be used in all subsequent non-equilibrium (NEQ) calculations. It is important to note that solving the non-equilibrium BSE is not feasible within the GW plasmon pole approximation. To address this limitation, we will instead solve the BSE for the equilibrium case and apply corrections to the energy values using a non-equilibrium COHSEX calculation.
The QP band structure will show the effect of the screened electron-electron interaction, while the absorption spectrum within the BSE accounts for the effect of the electron-hole interaction. When QP corrections are not available, they can be included using the scissor operator KfnQP_E, and the numerical values for "corrections" can be deduced from a GW calculation. For more information about solving the Equilibrium BSE equation refer to the following tutorial: Calculating optical spectra including excitonic effects: a step-by-step guide
- Equilibrium BSE Calculation (Demonstrative)
- Generating non-equilibrium carriers
- Equilibrium and non-equilibrium COHSEX calculations
- Calculation of QP-PPA corrections to Silicon (Optional)
- Non-Equilibrium BSE Calculation
Equilibrium optical properties
In this part, we will solve the equilibrium BSE calculation without quasiparticle corrections.
Enter the folder 8x8x8, and initialize yambo in the respective folder
$ cd 8x8x8 $ yambo
Static screening at equilibrium
First, to solve the BSE equation we need to calculate the statically screened electron-electron interaction (W), which is related to static dielectric screening [math]\displaystyle{ \epsilon^{-1} }[/math].
To do this create the following input file:
$ yambo -X s -F 01_EQ_BSE_screening.in
with the following contents:
em1s # [R][Xs] Statically Screened Interaction
% BndsRnXs
1 | 30 | # [Xs] Polarization function bands
%
NGsBlkXs= 3 Ry # [Xs] Response block size
% LongDrXs
1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field
%
Where we changed the response block size NGsBlkXs = 3 Ry and number of polarization function bands BndsRnXs to be in the range of 1 to 30. Now run the file:
$ yambo -F 01_EQ_BSE_screening.in -J EQ_BSE
Solving the Bethe-Salpeter equation
To solve the (equilibrium) Bethe-Salpeter equation, the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. For a non spin-polarized system and in the [math]\displaystyle{ q = 0 }[/math] limit, the two-particle Hamiltonian matrix elements are given by:
where [math]\displaystyle{ vc\mathbf{k} }[/math] indicates the pair of quasiparticle states [math]\displaystyle{ v\mathbf{k} }[/math] and [math]\displaystyle{ c\mathbf{k} }[/math]. The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part V (which stems from the Hartree potential) and the electron-hole attraction part W (which stems from the screened exchange potential). The electron-hole attraction part W, depends on [math]\displaystyle{ \epsilon^{-1} }[/math] which was calculated in the previous section. Please note that for the NEQ case, the Hamiltonian will take a different form, this will be discussed in the respective chapter.
After calculating the equilibrium Bethe-Salpeter kernel, the resulting two-particle Hamiltonian can be diagonalized to compute the macroscopic dielectric function, which can be used to get absorption and EELS spectra. Calculation of BS kernel and diagonalization of Hamiltonian can be done in one step.
To generate the input file for the calculation of BSE kernel, run the following command:
$ yambo -o b -k sex -F 02_EQ_BSE_kernel_diag.in -y h -J EQ_BSE
with the following input
optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. K_Threads=0 # [OPENMP/BSK] Number of threads for response functions BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "h" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 2085 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] % BSEQptR 1 | 1 | # [BSK] Transferred momenta range % % BSEBands 2 | 7 | # [BSK] Bands range % % BEnRange 2.20000 | 5.00000 | eV # [BSS] Energy range % % KfnQP_E 0.70000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 200 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field versor % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/asymm/anHAll/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane
Where BSEBands was changed to include bands from 2 to 7, which defines the basis of quasiparticle pairs that are used to describe excitons. 3 degenerate valence and 3 degenerate conduction bands where included. BEnRange was changed to 2.2-5.5 eV to match experimental data, and BEnSteps was increased from 100 to 200. The scissors operator KfnQP_E was used to match the possiton calculated spectra with experimental values. The Haydock BSE solver was chosen, -y h option, because it is substantially cheaper than the full diagonalization (quadratic with the number of electron-hole pairs). However, this approach does not provide the individual exciton energies and composition in terms of electron-hole pairs. The BSE solvers overview page can provide more info on the subject.
To run the file:
$ yambo -F 02_EQ_BSE_kernel_diag.in -J EQ_BSE
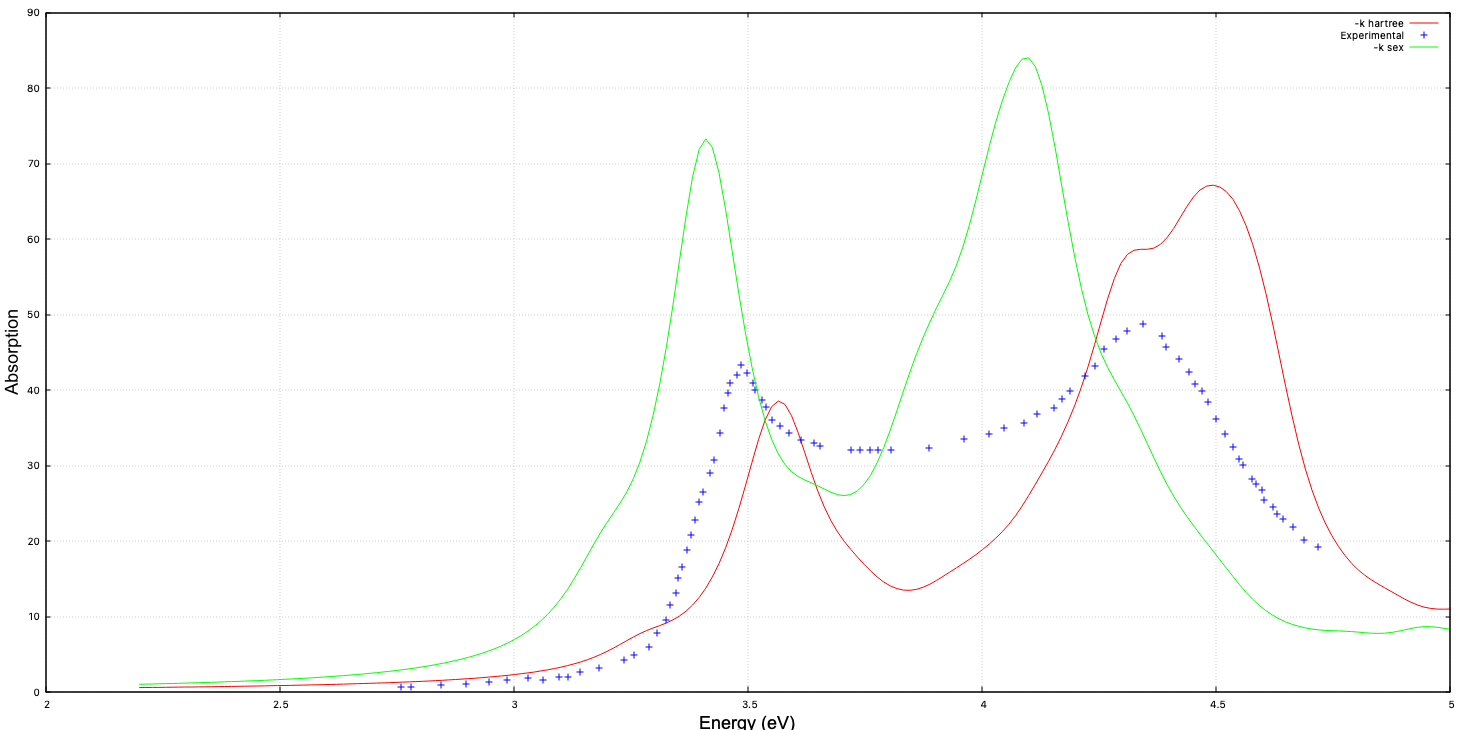
After the calculation has finished, the absorption spectra can be plotted with the following:
$ gnuplot ... gnuplot> set x label "Energy (eV)" gnuplot> set y label "Absorption" gnuplot> plot 'o-EQ_BSE.eps_q1_diago_bse' u 1:2 w l t '-k sex'
and the following plot will results (the "experimental" and "-k hartree" plots are added additionally for comparison)
Generating non-equilibrium carriers
To simulate non-equilibrium absorption, we need to define the number of non-equilibrium carriers, specifically electrons in the conduction band and holes in the valence band. These carriers follow the Fermi-Dirac distribution given by:
Here:
- E is the energy level,
- [math]\displaystyle{ \mu }[/math] is the chemical potential (specific to electrons or holes),
- [math]\displaystyle{ T }[/math] is the effective temperature,
- [math]\displaystyle{ k_B }[/math] is the Boltzmann constant.
For the simulation, both electrons and holes are characterized by their own [math]\displaystyle{ \mu_i }[/math] and [math]\displaystyle{ T_i }[/math] .
The distribution of non-equilibrium carriers can be generated using Yambo’s post processing for real-time module (ypp_rt), which allows modeling of these conditions.
To generate to non-equilibrium carriers databases create input_ypp1 input_ypp2 files, with the following content:
RTDBs # [R] Real-Time databases Select_Fermi # [R] NEQ DBs according to Fermi distribution % RTBands 1 | 8 | # [RT] Bands range % % RTmuEh -0.80 | 0.80 | eV # [RT] Chemical potentials hole | electron % % RTtempEh 0.04 | 0.04 | eV # [RT] Effective temperature hole | electron % RTautotuneThr= 0.000100 # [RT] Threshold to match no. of pumped holes and electrons.
RealTime # [R] Real-Time Post-Processing RToccupations # [R] Analize time-dependent occupations RTenergy # [R] Post-Processing kind: function of energy TimeStep= 0.000000 fs # Time step % TimeRange -1.000000 |-1.000000 | fs # Time-window where processing is done % #IncludeEQocc # [NEGF] Include also equilibrium occupations #SkipFermiFIT # [NEGF] Do a Fermi Fit of occupations (and lifetimes ratio) %QPkrange # generalized Kpoint/Band indices 1| 3| 1|8| %
And then run the files:
$ ypp_rt $ ypp_rt -F input_ypp1 -J carriers -C carriers $ ypp_rt -F input_ypp2 -J carriers -C carriers
The file input_ypp1 will generate a ndb.RT_carriers database which will contain the Fermi distribution of the electrons and the hole according to the specified chemical potential, RTmuEh, and for a specific temperature given by RTtempEh. The file input_ypp2 will generate a series of databases to plot different different aspects of the distribution.
Energy shift in the band structure
The GW method is the standard approach to compute quasi-particle corrections. However, in presence of non-equilibrium carriers, or even at finite temperature the formulation of the GW self-energy needs to be refined. This is due to its frequency dependence, which results in extra terms when performing the analytic continuation from the Keldish contour (non-equilibrium case) or from the Matsubara axis (finite temperature case) to the real time/frequency axis. See for example this reference [2] for the finite temperature case. On the other hand the COHSEX self-energy, being static, avoids this complication. This is why we will compute changes in the QP corrections within the COHSEX approximation.
To compute the Non-Equilibrium Absorption Spectra, we need to diagonalize a previously defined two-particle Hamiltonian. To account for the Non-Equilibrium effect, the Kohn-Sham energies, [math]\displaystyle{ \varepsilon_{c\mathbf{k}}, \varepsilon_{v\mathbf{k}} }[/math], calculated at the DFT level, need to be corrected. This requires calculating the following: COHSEX self-energy at equilibrium, COHSEX self-energy at non-equilibrium, and Equilibrium GW self-energy at Plasmon-Pole Approximation level.
Using these, the energy correction, [math]\displaystyle{ \varepsilon^{corr,neq} }[/math], can be computed as:
[math]\displaystyle{ \Large \varepsilon^{corr,neq}_{c\mathbf{k}} = \varepsilon^{GW,eq}_{c\mathbf{k}} + (\varepsilon^{cohsex,neq}_{c\mathbf{k}} - \varepsilon^{cohsex,eq}_{c\mathbf{k}}) }[/math]
The KS energies will be corrected as follows:
[math]\displaystyle{ \Large \varepsilon^{KS,neq}_{c\mathbf{k}} = \varepsilon_{c\mathbf{k}} + \varepsilon^{corr,neq}_{c\mathbf{k}} }[/math]
These corrected KS energies will be used when diagonalizing the two-particle Hamiltonian.
COHSEX corrections at equilibrium
To make a COHSEX calculation at equilibrium, we do the following:
$ yambo -p c -F 03_eq_cohsex.in
which will create a file with the following content:
gw0 # [R] GW approximation cohsex # [R][Xp] COlumb Hole Screened EXchange dyson # [R] Dyson Equation solver el_el_corr # [R] Electron-Electron Correlation HF_and_locXC # [R] Hartree-Fock em1s # [R][Xs] Statically Screened Interaction dipoles # [R] Oscillator strenghts (or dipoles) DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy EXXRLvcs= 2085 RL # [XX] Exchange RL components VXCRLvcs= 2085 RL # [XC] XCpotential RL components Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc % BndsRnXs 1 | 10 | # [Xs] Polarization function bands % NGsBlkXs= 1 RL # [Xs] Response block size UseEbands % GbndRnge 1 | 40 | # [GW] G[W] bands range % % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field % %QPkrange # [GW] QP generalized Kpoint/Band indices 1|1|2|7| %
Where the number of Polarization function bands, BndsRnXs was changed from 1|50 to 1|10, and the quasi-particles generalized Kpoint and Band indices,QPkrange, was changed from 1|29|1|50 to 1|1|2|7. Additionally the following lines were added
UseEbands % GbndRnge 1 | 40 | # [GW] G[W] bands range %
to force Yambo to do a calculation where self-energy depends on the conduction bands too, or this is also known as COHSEX with empty bands. Alternatively, an option option -V qp can be added when generating the file, but it will include a lot of redundant variables.
And after it we run the file with the following command:
$ yambo_rt -F 03_eq_cohsex.in -J cohsex_eq_emp -C cohsex_eq_emp
COHSEX corrections in presence of non-equilibrium carriers
Before making a COHSEX calculation, we need to recalculate the static screening in the presence of non-equilibrium carriers. After it, we can make a COHSEX calculation in the presence of non-equilibrium carriers using the ndb.RT_carriers database generated in the previous step with the ypp_rt module. To do this, we do the following:
$ yambo -p c -F 03_neq_cohsex.in
where we need to add the following lines:
XfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" GfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers"
and the resulting file is:
gw0 # [R] GW approximation cohsex # [R][Xp] COlumb Hole Screened EXchange dyson # [R] Dyson Equation solver el_el_corr # [R] Electron-Electron Correlation HF_and_locXC # [R] Hartree-Fock em1s # [R][Xs] Statically Screened Interaction dipoles # [R] Oscillator strenghts (or dipoles) DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy EXXRLvcs= 2085 RL # [XX] Exchange RL components VXCRLvcs= 2085 RL # [XC] XCpotential RL components Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc % BndsRnXs 1 | 10 | # [Xs] Polarization function bands % UseEbands % GbndRnge 1 | 40 | # [GW] G[W] bands range % NGsBlkXs= 1 RL # [Xs] Response block size % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field % %QPkrange # [GW] QP generalized Kpoint/Band indices 1|1|2|7| %
where we added the respective two lines with XfnRTdb, and GfnRTdb, and made changes to BndsRnXs and QPkrange similar to the equilibrium case. Additionally, we added the lines to force Yambo to do a COHSEX calculation with empty bands.
The line
> em1s # [R][Xs] Statically Screened Interaction
will tell Yambo to make the static screening calculation, and the lines:
> gw0 # [R] GW approximation > cohsex # [R][Xp] COlumb Hole Screened EXchange
will tell Yambo to do make a COHSEX calculation.
After it we can run the file with the command:
$ yambo_rt -F 03_neq_cohsex.in -J cohsex_neq -C cohsex_neq
GW PPA corrections for the equilibrium case
This subchapter can be skipped, and replaced by using scissors operator when diagonalizing the two particle Hamiltonian.
To get accurate values for the band gap value we need to go beyond COHSEX approximation. Therefore we will obtain the Quasi-particle corrections in the plasmon pole approximation for equilibrium case, and in next steps, to this value we will add the correction calculated at COHSEX approximation to account for the non-equilibrium state of the system.
To make this calculation, we do the following:
$ yambo -p p -F 03_eq_qp_ppa.in
which will create a file with the following content:
gw0 # [R] GW approximation
ppa # [R][Xp] Plasmon Pole Approximation for the Screened Interaction
el_el_corr # [R] Electron-Electron Correlation
HF_and_locXC # [R] Hartree-Fock
em1d # [R][X] Dynamically Screened Interaction
X_Threads=0 # [OPENMP/X] Number of threads for response functions
DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy
EXXRLvcs= 2085 RL # [XX] Exchange RL components
VXCRLvcs= 2085 RL # [XC] XCpotential RL components
Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% BndsRnXp
1 | 10 | # [Xp] Polarization function bands
%
NGsBlkXp= 1 RL # [Xp] Response block size
% LongDrXp
1.000000 | 0.000000 | 0.000000 | # [Xp] [cc] Electric Field
%
PPAPntXp= 27.21138 eV # [Xp] PPA imaginary energy
% GbndRnge
1 | 10 | # [GW] G[W] bands range
%
GTermKind= "none" # [GW] GW terminator ("none","BG" Bruneval-Gonze,"BRS" Berger-Reining-Sottile)
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g","q")
%QPkrange # [GW] QP generalized Kpoint/Band indices
1|8|1|10|
%
where the following changes have been made: the number of polarization function bands, BndsRnXp was changed from 1|50 to 1|10, the G[W] bands range, GbndRnge was changed from 1|50 to 1|10, and quasi-particle generalized k points and band indices, QPkrange was changed from 1|29|1|50 to 1|8|1|10. And after it we run the file:
$ yambo_rt -F 03_eq_qp_ppa.in -J gw_eq -C gw_eq
Data post-processing
Now after obtaining all the energy components that we need to calculate corrections to Kohn-Sham energies for the Non-Equilibrium case, we can manipulate them using the yambo's real time post processing module, ypp_rt. We want to obtain energies defined by the following equation:
[math]\displaystyle{ \Large \varepsilon^{corr,neq}_{c\mathbf{k}} = \varepsilon^{GW,eq}_{c\mathbf{k}} + (\varepsilon^{cohsex,neq}_{c\mathbf{k}} - \varepsilon^{cohsex,eq}_{c\mathbf{k}}) }[/math].
Therefore we create a yambo post processing file with the following contents:
QPDBs # [R] Quasi-particle databases QPDB_merge # [R] Mergering %Actions_and_names # [QPDB] QP databases and Actions (format is "what"|"OP"|"prefactor"|"DB"|). OP can be ±/x. "E" | "+" | "1" | "cohsex_neq/ndb.QP" | "E" | "-" | "1" | "cohsex_eq_emp/ndb.QP" | "Z" | "+" | "1" | "gw_eq/ndb.QP" | "E" | "+" | "1" | "08_gw_eq/ndb.QP" | %
where we tell ypp to take from the quasi particle correction databases the values of [math]\displaystyle{ \varepsilon^{cohsex,neq}_{c\mathbf{k}} }[/math] subtract from them [math]\displaystyle{ \varepsilon^{cohsex,eq}_{c\mathbf{k}} }[/math], multiply the resulting value by ????? and add it to [math]\displaystyle{ \varepsilon^{GW,eq}_{c\mathbf{k}} }[/math] and save them in the the new database ndb.QP_merged_1_gw_cohsex_gw_ppa.
We run the file by the following command:
$ ypp_rt -F input_ypp3 -J QP_merge -C QP_merge
Or alternatively, if no calculation for the quasiparticle correction has been made (except the COHSEX calculation), and a scissors operator is going to be used, we can use the following yambo post processing file:
QPDBs # [R] Quasi-particle databases QPDB_merge # [R] Mergering %Actions_and_names # [QPDB] QP databases and Actions (format is "what"|"OP"|"prefactor"|"DB"|). OP can be ±/x. "E" | "+" | "1" | "cohsex_neq/ndb.QP" | "E" | "-" | "1" | "cohsex_eq_emp/ndb.QP" | %
which will just take from the quasi particle correction databases the values of [math]\displaystyle{ \varepsilon^{cohsex,neq}_{c\mathbf{k}} }[/math] subtract from them [math]\displaystyle{ \varepsilon^{cohsex,eq}_{c\mathbf{k}} }[/math]. And we run this file by:
$ ypp_rt -F input_ypp3_scissors -J QP_merge_shissor -C QP_merge_shissor
Renormalization of the exciton binding energy
We finally perform a BSE calculation loading both the nonequilibrium carriers and the quasi-particle energy shifts.
We create a file using the following command:
$ yambo -o b -y d -V qp -F 04_neq_bse.in
With GW qp corrections
where we add the lines:
XfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" RTOccMode="KR" KfnQPdb= "E < QP_merge/ndb.QP_merged_1_gw_cohsex_gw_ppa"
the resulting structure of the file is:
bss # [R] BSE solver optics # [R] Linear Response optical properties dipoles # [R] Oscillator strenghts (or dipoles) bse # [R][BSE] Bethe Salpeter Equation. DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 2085 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] #WehCpl # [BSK] eh interaction included also in coupling KfnQPdb= "none" # [EXTQP BSK BSS] Database action KfnQP_INTERP_NN= 1 # [EXTQP BSK BSS] Interpolation neighbours (NN mode) KfnQP_INTERP_shells= 20.00000 # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode) KfnQP_DbGd_INTERP_mode= "NN" # [EXTQP BSK BSS] Interpolation DbGd mode % KfnQP_E 0.000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % KfnQP_Z= ( 1.000000 , 0.000000 ) # [EXTQP BSK BSS] Z factor (c/v) KfnQP_Wv_E= 0.000000 eV # [EXTQP BSK BSS] W Energy reference (valence) % KfnQP_Wv 0.000000 | 0.000000 | 0.000000 | # [EXTQP BSK BSS] W parameters (valence) eV| 1|eV^-1 % KfnQP_Wv_dos= 0.000000 eV # [EXTQP BSK BSS] W dos pre-factor (valence) KfnQP_Wc_E= 0.000000 eV # [EXTQP BSK BSS] W Energy reference (conduction) % KfnQP_Wc 0.000000 | 0.000000 | 0.000000 | # [EXTQP BSK BSS] W parameters (conduction) eV| 1 |eV^-1 % XfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnQPdb= "E < QP_merge/ndb.QP_merged_1_gw_cohsex_gw_ppa" RTOccMode="KR" KfnQP_Wc_dos= 0.000000 eV # [EXTQP BSK BSS] W dos pre-factor (conduction) % BSEQptR 1 | 1 | # [BSK] Transferred momenta range % % BSEBands 2 | 7 | # [BSK] Bands range % % BEnRange 2.00000 | 6.00000 | eV # [BSS] Energy range % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 200 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field versor % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/asymm/anHAll/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane #WRbsWF # [BSS] Write to disk excitonic the WFs
where we added the lines, and changed the bands range, BSEBands from 1|50 to 2|7, energy range, BEnRange from 0.00000 | 10.00000 to 2.00000 | 10.00000 | and energy steps, BEnSteps from 100 to 200. And we run the file:
$ yambo -F 04_neq_bse.in -J "neq_bse,gw_eq"
Alternatively, when scissors are used, the lines can be added, to account for the lack of a proper GW correction.
With shissor corrections
where we add the lines:
XfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" RTOccMode="KR" % KfnQP_E 0.70000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) % KfnQPdb= "E < QP_merge_shissor/ndb.QP_merged_1_gw_cohsex"
the resulting structure of the file is:
bss # [R] BSE solver optics # [R] Linear Response optical properties dipoles # [R] Oscillator strenghts (or dipoles) bse # [R][BSE] Bethe Salpeter Equation. DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 2085 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] #WehCpl # [BSK] eh interaction included also in coupling % KfnQP_E 0.700000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % XfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnRTdb= "f @ 0. ps < carriers/ndb.RT_carriers" KfnQPdb= "E < QP_merge/ndb.QP_merged_1_gw_cohsex" RTOccMode="KR" % BSEQptR 1 | 1 | # [BSK] Transferred momenta range % % BSEBands 2 | 7 | # [BSK] Bands range % % BEnRange 2.00000 | 6.00000 | eV # [BSS] Energy range % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 200 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field versor % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/asymm/anHAll/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane #WRbsWF # [BSS] Write to disk excitonic the WFs
where we added the lines, and changed the bands range, BSEBands from 1|50 to 2|7, energy range, BEnRange from 0.00000 | 10.00000 to 2.00000 | 10.00000 | and energy steps, BEnSteps from 100 to 200. And we run the file: