Second-harmonic generation of 2D-hBN: Difference between revisions
| Line 109: | Line 109: | ||
replot '01_SHG_ip_files/o-01_SHG_ip.polarization_F12' u 1:2 w l lw 2 title "omega = 7.375" | replot '01_SHG_ip_files/o-01_SHG_ip.polarization_F12' u 1:2 w l lw 2 title "omega = 7.375" | ||
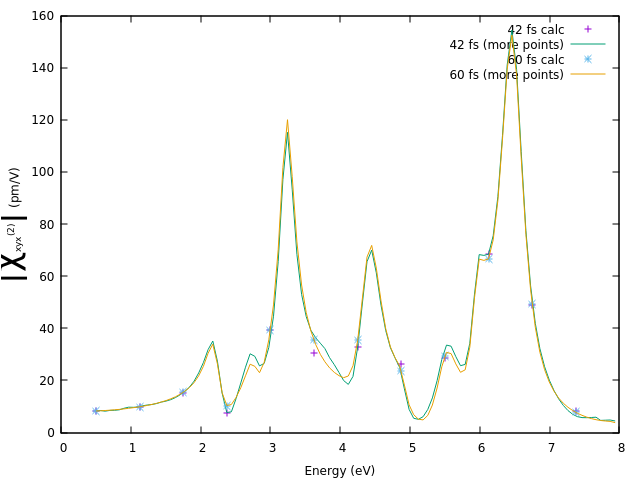
[[File:Comparison of the SHG intensity of 2D h-BN obtained with different simulation time.png|thumb|Yambo tutorial image]] | |||
TO DO: Add a plot of the polarization. Note that it is sinusoidal etc. and the nonlinear part is not visible since every order is as a rule of a thumb 6-7 orders of magnitude smaller than the previous. | TO DO: Add a plot of the polarization. Note that it is sinusoidal etc. and the nonlinear part is not visible since every order is as a rule of a thumb 6-7 orders of magnitude smaller than the previous. | ||
Revision as of 17:38, 24 May 2023
Step 0: Theoretical framework
In this tutorial, we compute the Second-harmonic generation (SHG) from the dynamics of the Bloch-states. The equation-of-motion of the Bloch-states is explained in the tutorial on Linear response from Bloch-states dynamics. Independently of the 'experiment' we simulate, the part of the integration of motion stays the same. This means that any experiment, including non-linear optics, can be performed at the level of the theory listed for the computation of the dielectric function:
- independent (quasi)particle
- time-dependent Hartree (RPA level)
- time-dependent DFT (and DPFT)
- time-dependent Hartree+Screened exchange (BSE level)
What changes when we want to calculate the SHG (or higher harmonics) is:
- the time-dependence of the input electric field and
- the post-processing of the signal
Time dependence of the electric Field: we choose a sinusoidal electric field, thus a monochromatic laser field. This allows one to expand the polarization in the form [math]\displaystyle{ \bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{p}_n e^{-i\omega_n t} }[/math] where the coefficient [math]\displaystyle{ \bf{p}_1,...,\bf{p}_n }[/math] are related to [math]\displaystyle{ \chi^{(1)},...,\chi^{(n)} }[/math] through a coefficient depending on a power of the strength of the field (with the power depending on the order of the response).
At difference with a delta-like perturbation, a real-time simulation gives the response at the laser-field only. Then, to obtain the spectrum for the desired range of frequency, we have to perform so many simulations as the frequencies in the desired range.
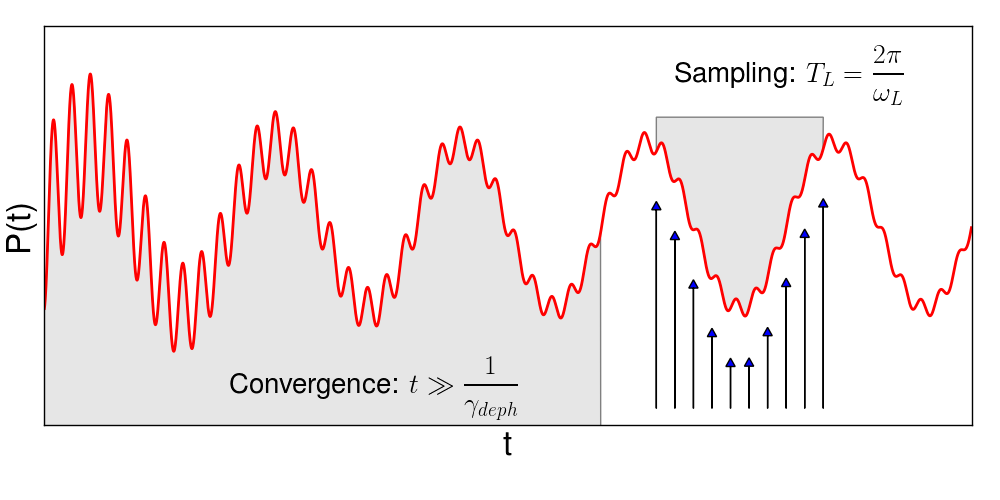
Post-processing of the signal: The switch-on of the electric field corresponds to a weak delta-like kick. Thus, even if it may not be noticeable, the polarization results from both the sinusoidal field and the delta-like kick. The latter excites all eigenfrequencies of the system. Though weak, the resulting signal is comparable with the second-harmonic signal. To eliminate the signal from the eigenfrequencies, we apply a dephasing ([math]\displaystyle{ \gamma_{deph} }[/math]). To have a signal useful to sample the second-harmonic signal, we need to wait a time [math]\displaystyle{ \bar t }[/math] much larger than the dephasing-time [math]\displaystyle{ 1/\gamma_{deph} }[/math]. Note that we cannot choose a too short dephasing time (to shorten the simulation time), as this would result in a too large broadening of the spectrum. After [math]\displaystyle{ \bar t }[/math], we sample $2N+1$ times in a period and use discrete Fourier transform to extract [math]\displaystyle{ {p}_n }[/math] for [math]\displaystyle{ n = 0,...,N }[/math], where n=2 gives the SHG. This is schematically illustrated in figure:
The scheme from Ref. [1] summarised the workflow for computing the SHG (or higher-harmonics) in a energy range [math]\displaystyle{ [\Omega_1,\Omega_2] }[/math].
Step 1: Prerequisites
In this example, we will consider a single layer of hexagonal boron nitride (hBN). Before running real time simulations to compute the SHG in yambo you need to download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz.
Unzip the tarball and change directory to YAMBO and run the setup (yambo_nl -nompi).
Execute the command
ypp_nl -fixsym -F 00_removesym.in
to create the input, to remove the symmetries which are not compatible with the field:
fixsyms # [R] Remove symmetries not consistent with an external perturbation % Efield1 1.000000 | 1.000000 | 0.000000 | # First external Electric Field % % Efield2 0.000000 | 0.000000 | 0.000000 | # Additional external Electric Field % BField= 0.000000 T # [MAG] Magnetic field modulus Bpsi= 0.000000 deg # [MAG] Magnetic field psi angle [degree] Btheta= 0.000000 deg # [MAG] Magnetic field theta angle [degree] #RmAllSymm # Remove all symmetries RmTimeRev # Remove Time Reversal #RmSpaceInv # Remove Spatial Inversion #KeepKGrid # Do not expand the k-grid
where we chose the field along the xy direction and we remove time-reversal symmetry.
Then run the pre-processing job:
ypp_nl -F 00_removesym.in J 00_removesym
This creates the directory FixSymm. Change directory to FixSymm. This contains the SAVE directory with reduced symmetries, compatible with the direction of the field.
Step 2: Independent-particle approximation
Use the command:
yambo_nl -nl n -F 01_SHG_ip.in
to generate the input:
nloptics # [R] Non-linear spectroscopy % NLBands 3 | 6 | # [NL] Bands range % NLverbosity= "high" # [NL] Verbosity level (low | high) NLtime=-1.000000 fs # [NL] Simulation Time NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.5000000 |8.000000 | eV # [NL] Energy range % NLEnSteps= 12 # [NL] Energy steps NLDamping= 0.200000 eV # [NL] Damping (or dephasing) RADLifeTime=-1.000000 fs # [RT] Radiative life-time (if negative Yambo sets it equal to Phase_LifeTime in NL) #EvalCurrent # [NL] Evaluate the current #FrPolPerdic # [DIP] Force periodicity of polarization respect to the external field HARRLvcs= 21817 RL # [HA] Hartree RL components EXXRLvcs= 21817 RL # [XX] Exchange RL components % Field1_Freq 0.100000 | 0.100000 | eV # [RT Field1] Frequency % Field1_NFreqs= 1 # [RT Field1] Frequency Field1_Int= 1000.00 kWLm2 # [RT Field1] Intensity Field1_Width= 0.000000 fs # [RT Field1] Width Field1_kind= "SIN" # [RT Field1] Kind(SIN|COS|RES|ANTIRES|GAUSS|DELTA|QSSIN) Field1_pol= "linear" # [RT Field1] Pol(linear|circular) % Field1_Dir 1.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor % Field1_Tstart= 0.010000 fs # [RT Field1] Initial Time
To describe the Bloch-dynamics we will use as a basis the KS-states 3-6 for the k-grid used in the non-scf DFT calculations, that is a 6x6x1 (NLBands). We choose 12 equally spaced frequencies (NLEnSteps) for the applied field in the range (NLEnRange) between 0.5 and 8 eV. We choose a sinusoidal time-dependence (Field1_kind) and set the field direction (Field1_kind) along xy. The negative simulation time (NLtime=-1.000000) means that the code will choose it based on the value of the NLDamping. While this is a good lower bound for the simulation time, one should check it is sufficient to get accurate results.
Run the simulation, possibly in parallel e. g. in a interactive session on 4 cores, execute the command:
mpirun -n 4 yambo_nl -F 01_SHG_ip.in -J 01_SHG_ip -C 01_SHG_ip_files
Once the run is finished, check the report 01_SHG_ip_files/r-01_SHG_ip_nloptics. In particular, in the appended input files, you can see the default parallelization applied by the code for calculating the dipoles and run the time-propagation. For the latter, the main parallelization is on the frequencies and then on the k-points (NL_ROLEs= "w.k").
| NL_CPU= "2.2" # [PARALLEL] CPUs for each role | NL_ROLEs= "w.k" # [PARALLEL] CPUs roles (w,k) | DIP_CPU= "2.2.1" # [PARALLEL] CPUs for each role | DIP_ROLEs= "v.c.k" # [PARALLEL] CPUs roles (k,c,v)
Plot the polarization for a couple of frequencies, e.g. the first and last of the chosen range (the corresponding frequency can be read in the file, search for "Frequency value"):
set ylabel "x-component polarization" offset -0.7 set xlabel "time (fs)" plot '01_SHG_ip_files/o-01_SHG_ip.polarization_F1' u 1:2 w l lw 2 title "omega = 0.5 eV" replot '01_SHG_ip_files/o-01_SHG_ip.polarization_F12' u 1:2 w l lw 2 title "omega = 7.375"
TO DO: Add a plot of the polarization. Note that it is sinusoidal etc. and the nonlinear part is not visible since every order is as a rule of a thumb 6-7 orders of magnitude smaller than the previous.
Output post-processing: the dielectric function
Once we obtained the polarization, we Fourier-transform the polarization to obtain the dielectric function.
Use the command:
ypp_nl -u -F Inputs_shg/ypp_shg.in
to generate the input file (THIS IS A PLACEHOLDER):
nonlinear # [R] NonLinear Optics Post-Processing Xorder= 1 # Max order of the response functions % TimeRange -1.000000 |-1.000000 | fs # Time-window where processing is done % ETStpsRt= 1001 # Total Energy steps % EnRngeRt 0.00000 | 10.00000 | eV # Energy range % DampMode= "LORENTZIAN" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) DampFactor= 0.10000 eV # Damping parameter
TO-DO: describe the main keys and parameters.
To run the post-processing, use the command:
ypp_nl -F Inputs_shg/ypp_shg.in -J TD-IP_nl -C TD-IP_nl
TO-DO describe which files are produced
TO-DO: Plot the SHG and comments
Step 3: Hartree+Screened exchange approximation (BSE level)
References
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)