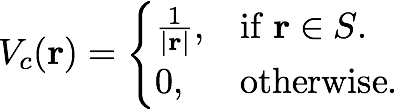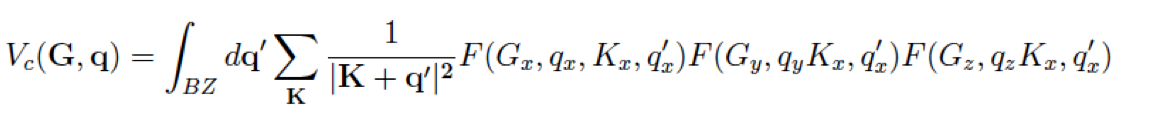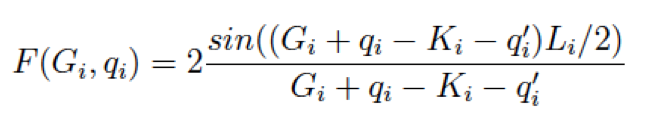How to treat low dimensional systems: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
In this tutorial you will learn for a low-dimensional (2D) material how to: | In this tutorial you will learn for a low-dimensional (2D) material how to: | ||
* Avoid numerical | * Avoid numerical divergences using the Random Integration Method (RIM) | ||
* Generate a truncated coulomb potential with a box-like cutoff to eliminate the image-image interactions | * Generate a truncated coulomb potential with a box-like cutoff to eliminate the image-image interactions | ||
* Use the truncated coulomb potential in the GW calculation | * Use the truncated coulomb potential in the GW calculation | ||
| Line 15: | Line 15: | ||
==Avoid numerical | ==Avoid numerical divergences using the Random Integration Method (RIM)== | ||
In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) | In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) | ||
This can create numerical problems in the convergence of the many-body results due to the divergence of the coulomb potential | This can create numerical problems in the convergence of the many-body results due to the divergence at small q of the coulomb potential | ||
(which appears in all the main equations, see i.e. the exchange self-energy equation) | (which appears in all the main equations, see i.e. the exchange self-energy equation). | ||
To eliminate this problem YAMBO uses the so-called Random Integration Method | To eliminate this problem YAMBO uses the so-called Random Integration Method | ||
| Line 26: | Line 26: | ||
$ yambo -F yambo_RIM.in -r | $ yambo -F yambo_RIM.in -r | ||
and change the following variable | |||
RandQpts= 1000000 # [RIM] Number of random q-points in the BZ | RandQpts= 1000000 # [RIM] Number of random q-points in the BZ | ||
RandGvec= 1 RL # [RIM] Coulomb interaction RS components | RandGvec= 1 RL # [RIM] Coulomb interaction RS components | ||
N.B RandGvec=1 means to use RIM only for the G=0 but higher G-components can be treated with the same RIM approach | |||
(in principle convergence of the observables should be checked). | |||
Close input and Run yambo | Close input and Run yambo | ||
| Line 34: | Line 38: | ||
$ yambo -F yambo_RIM.in -J 2D | $ yambo -F yambo_RIM.in -J 2D | ||
At the end in the 2D directory you find a new database ndb.RIM | At the end in the 2D directory you find a new database ndb.RIM. | ||
A new report file r-2D_rim_cut is present. Open it and look inside | |||
[04.02] RIM integrals | [04.02] RIM integrals | ||
| Line 63: | Line 68: | ||
Calculation of the HF gap reading the RIM database | |||
$ yambo -F yambo_cut2D.in -x -r -J 2D | $ yambo -F yambo_cut2D.in -x -r -J 2D | ||
Inside the input change the last line as (to calculate the correction only in the last point | Inside the input change the last line as (to calculate the correction only in the last point for the VBM and CBM only. | ||
%QPkrange # [GW] QP generalized Kpoint/Band indices | %QPkrange # [GW] QP generalized Kpoint/Band indices | ||
7| 7| 4| 5| | 7| 7| 4| 5| | ||
Close the input and run yambo. You will find the report file r-2D | Close the input and run yambo. You will find the report file r-2D_HF_and_locXC_rim_cut and the output file o-2D.hf | ||
which reports the calculated HF energies. | |||
# K-point Band Eo Ehf DFT HF | |||
# | |||
7.00000 4.00000 0.00000 -3.12300 -16.21949 -19.34249 | |||
7.00000 5.00000 4.40109 9.72562 -11.10752 -5.78299 | |||
# | |||
with an HF gap of 12.85 eV | |||
Revision as of 18:47, 27 March 2017
In this tutorial you will learn for a low-dimensional (2D) material how to:
- Avoid numerical divergences using the Random Integration Method (RIM)
- Generate a truncated coulomb potential with a box-like cutoff to eliminate the image-image interactions
- Use the truncated coulomb potential in the GW calculation
- Use the truncated coulomb potential in the BSE calculation
- Analyze the difference with corresponding calculations without the use of a truncated potetnial
Prerequisites
- Complete the Generating the Yambo databases tutorial
SAVEfolder for 2D hBN.yamboexecutableyppexecutable- Run Initialization
Avoid numerical divergences using the Random Integration Method (RIM)
In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) This can create numerical problems in the convergence of the many-body results due to the divergence at small q of the coulomb potential (which appears in all the main equations, see i.e. the exchange self-energy equation).
To eliminate this problem YAMBO uses the so-called Random Integration Method which means to use a Monte Carlo Integration with Random Q-points whose number RandQpts is given in input.
Create the input to generate the ndb.RIM database
$ yambo -F yambo_RIM.in -r
and change the following variable
RandQpts= 1000000 # [RIM] Number of random q-points in the BZ RandGvec= 1 RL # [RIM] Coulomb interaction RS components
N.B RandGvec=1 means to use RIM only for the G=0 but higher G-components can be treated with the same RIM approach
(in principle convergence of the observables should be checked).
Close input and Run yambo
$ yambo -F yambo_RIM.in -J 2D
At the end in the 2D directory you find a new database ndb.RIM. A new report file r-2D_rim_cut is present. Open it and look inside
[04.02] RIM integrals =====================
Gamma point sphere radius [au]: 0.08028
Points outside the sphere : 799738
[Int_sBZ(q=0) 1/q^2]*(Vol_sBZ)^(-1/3) = 7.659063
should be < 7.795600
[WR./2D//ndb.RIM]-------------------------------------------
Brillouin Zone Q/K grids (IBZ/BZ): 7 36 7 36
Coulombian RL components : 1
Coulombian diagonal components :yes
RIM random points : 1000000
RIM RL volume [a.u.]: 0.389358
Real RL volume [a.u.]: 0.390112
Eps^-1 reference component :0
Eps^-1 components : 0.00 0.00 0.00
RIM anysotropy factor : 0.000000
- S/N 005962 -------------------------- v.04.01.02 r.00120 -
Summary of Coulomb integrals for non-metallic bands |Q|[au] RIM/Bare:
Q [1]:0.1000E-40.9825 * Q [2]: 0.256404 1.092017 Q [5]: 0.444104 1.029665 * Q [3]: 0.512807 1.021649 Q [6]: 0.678380 1.011520 * Q [4]: 0.769211 1.008251 Q [7]: 0.888208 1.005896
Calculation of the HF gap reading the RIM database
$ yambo -F yambo_cut2D.in -x -r -J 2D
Inside the input change the last line as (to calculate the correction only in the last point for the VBM and CBM only.
%QPkrange # [GW] QP generalized Kpoint/Band indices
7| 7| 4| 5|
Close the input and run yambo. You will find the report file r-2D_HF_and_locXC_rim_cut and the output file o-2D.hf which reports the calculated HF energies.
- K-point Band Eo Ehf DFT HF
7.00000 4.00000 0.00000 -3.12300 -16.21949 -19.34249 7.00000 5.00000 4.40109 9.72562 -11.10752 -5.78299
with an HF gap of 12.85 eV
Unfortunately the presence of the numerical instability is evident only using denser k-grids with respect to that one
used in this Tutorial (6x6x1).
To see it you should generate other SAVE directories with denser k-grids and check i.e. the HF gap.
Here we report the HF gap calculated with different k-grids without (noRIM) and with Random Inetgration Method (RIM) to show the problem.
noRIM RIM 6x6x1 12x12x1 15x15x1 45x45x1
So home message : use always the RIM in MB simulations of low-dimensional materials.
Generate a truncated coulomb potential/ndb.cutoff database (yambo -r)
To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. ) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.
In YAMBO you can use :
spherical cutoff (for 0D systems) cylindrical cutoff (for 1D systems) box-like cutoff (for 0D, 1D and 2D systems)
The Coulomb potential with a box-like cutoff is defined as
Then the FT component is
where
For a 2D-system with non period direction along z-axis we have
Important remarks:
- the Random Integration Method (RIM) is required to perform the Q-space integration
- for sufficiently large supercells a choose L_i slightly smaller than the cell size in the i-direction ensures to avoid interaction between replicas
Creation of the input file:
$ yambo -F yambo_cut2D.in -r
Open the input file yambo_cut2D.in
Change the variables inside as:
RandQpts= 1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components
CUTGeo= "box z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. % CUTBox 0.00 | 0.00 | 32.0 | # [CUT] [au] Box sides
Close the input file
Run yambo:
$ yambo -F yambo_cut2D.in -J 2D
in the directory 2D you will find the two new databases
ndb.RIM ndb.cutoff