Real time approach to linear response: Difference between revisions
(Prepared section on yambo_rt) |
|||
| Line 1: | Line 1: | ||
In this example, we will consider a single layer of hexagonal boron nitride (hBN). If you didn't before you can download input files and Yambo databases for this tutorial here: [http://www.yambo-code.org/educational/tutorials/files/hBN-2D-RT.tar.gz hBN-2D-RT.tar.gz]. | In this example, we will consider a single layer of hexagonal boron nitride (hBN). | ||
If you didn't before you can download input files and Yambo databases for this tutorial here: [http://www.yambo-code.org/educational/tutorials/files/hBN-2D-RT.tar.gz hBN-2D-RT.tar.gz]. | |||
and/or follow the instructions to generate the databases here: [[Prerequisites for Real Time propagation with Yambo]] | |||
==Real-time dynamics == | |||
Since we work with the two independent approaches coded in yambo it will be useful to create two different folders for the input files. | |||
mkdir Inputs_rt | |||
mkdir Inputs_nl | |||
In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field. | |||
== | ==Approach based on the density matrix == | ||
Use the command <code>yambo_rt -p p -F 01_td_ip.in</code> to generate the input: | |||
negf # [R] Real-Time dynamics | |||
RT_Threads=0 # [OPENMP/RT] Number of threads for real-time | |||
HXC_Potential= "IP" # [SC] SC HXC Potential | |||
% RTBands | |||
3 | 6 | # [RT] Bands | |||
% | |||
Integrator= "RK2" # [RT] Integrator. Use keywords space separated ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA") | |||
PhLifeTime= 0.000000 fs # [RT] Dephasing Time | |||
RTstep=10.000000 as # [RT] Real Time step length | |||
NETime= 55.00000 fs # [RT] Simulation Time | |||
% IOtime | |||
0.05 | 5.00 | 0.10 | fs # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT) | |||
% | |||
% Field1_Freq | |||
0.00 | 0.00 | eV # [RT Field1] Frequency | |||
% | |||
Field1_Int=1.E4 kWLm2 # [RT Field1] Intensity | |||
Field1_Width= 0.000000 fs # [RT Field1] Width | |||
Field1_kind= "DELTA" # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) | |||
Field1_pol= "linear" # [RT Field1] Pol(linear|circular) | |||
% Field1_Dir | |||
0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor | |||
% | |||
% Field1_Dir_circ | |||
0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor_circ | |||
% | |||
Field1_Tstart= 0.000000fs # [RT Field1] Initial Time | |||
Set the field direction along y, the field type to <code>DELTA</code>, the length of the simulation to 55 fs, number of bands from 3 to 6, dephasing to zero and the field intensity to 1.E4. | |||
The <code>yambo_rt</code> is optimized for TD-SEX (or even more sophisticated calculations). The I/O time, which is negligible in such calculations, is less optimized and becomes the most time demanding step here. | |||
We can overcome this setting the IOtime for the polarization to 50 as (i.e. each 5 time steps). | |||
==Approach based on the Berry Phase == | |||
Use the command <code>yambo_nl -u -F input_lr.in</code> to generate the input: | |||
nlinear # [R NL] Non-linear optics | nlinear # [R NL] Non-linear optics | ||
| Line 36: | Line 76: | ||
The standard input of | The standard input of <code>yambo_nl</code> is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to <code>DELTA</code>, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red. | ||
We set the verbosity to "high" in such a way to print real-time output files. | We set the verbosity to "high" in such a way to print real-time output files. | ||
We set the differential equation integrator to <code>INVINT</code> that is faster but less accurate than the default (see Ref. <ref name="Attaccalite2013">C. Attaccalite and M. Gruning [https://arxiv.org/abs/1309.4012v2 Rev. B, '''88''', 235113 (2013)]</ref>) . This integrator is ok in case of independent | We set the differential equation integrator to <code>INVINT</code> that is faster but less accurate than the default (see Ref. <ref name="Attaccalite2013">C. Attaccalite and M. Gruning [https://arxiv.org/abs/1309.4012v2 Rev. B, '''88''', 235113 (2013)]</ref>) . This integrator is ok in case of independent particles but I advise you to use <code>CRANKNIC</code> integrator when correlation effects are present. Now run <code>yambo_nl -F input_lr.in</code> | ||
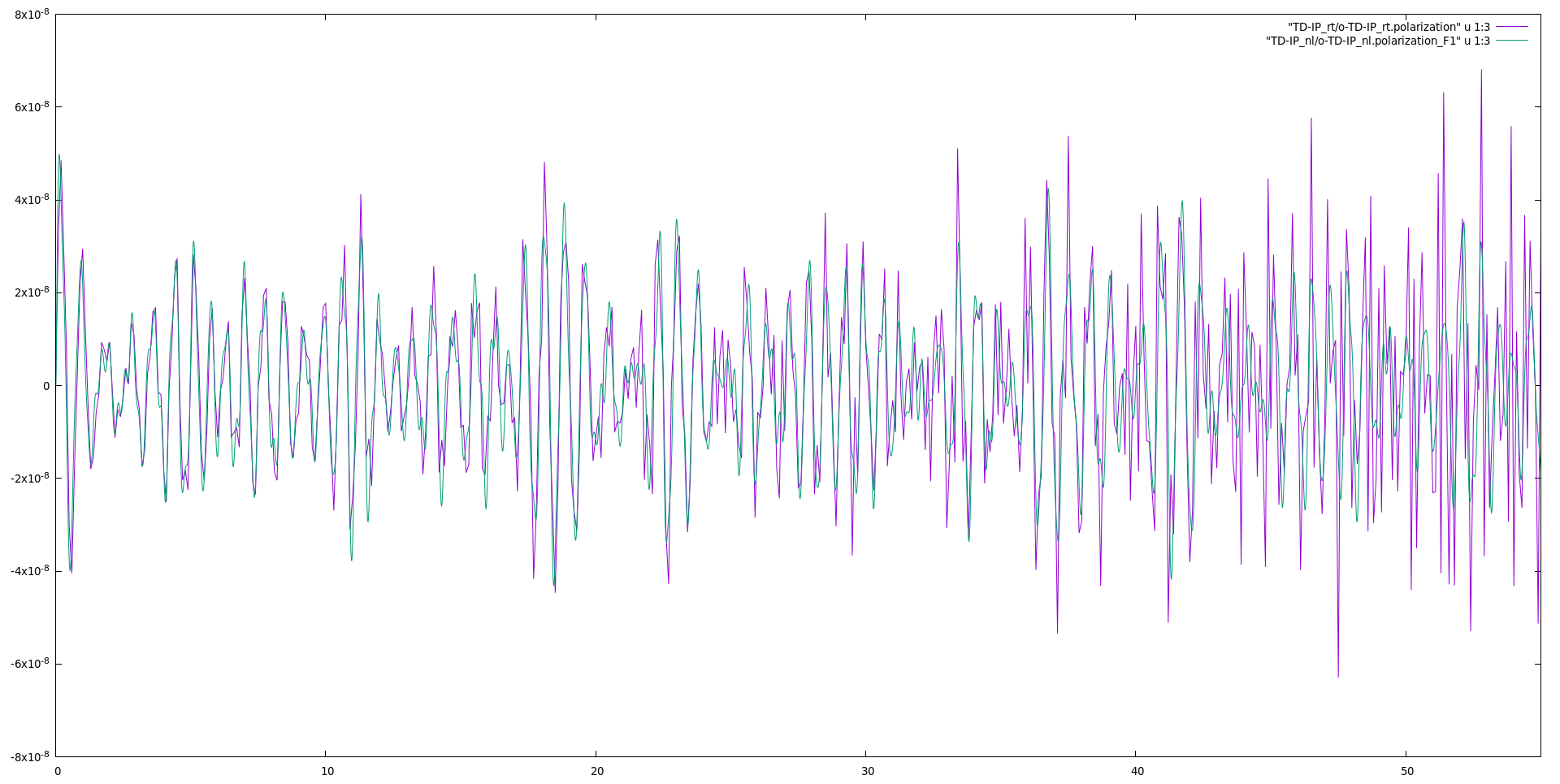
The code will produce different files: <code>o.polarization_F1</code> that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. If you plot the third column of <code>o.polarization_F1</code> versus the first one (time-variable) you will get the time-dependent polarization along the y-direction: | The code will produce different files: <code>o.polarization_F1</code> that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. If you plot the third column of <code>o.polarization_F1</code> versus the first one (time-variable) you will get the time-dependent polarization along the y-direction: | ||
Revision as of 14:59, 20 January 2020
In this example, we will consider a single layer of hexagonal boron nitride (hBN). If you didn't before you can download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz. and/or follow the instructions to generate the databases here: Prerequisites for Real Time propagation with Yambo
Real-time dynamics
Since we work with the two independent approaches coded in yambo it will be useful to create two different folders for the input files.
mkdir Inputs_rt mkdir Inputs_nl
In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field.
Approach based on the density matrix
Use the command yambo_rt -p p -F 01_td_ip.in to generate the input:
negf # [R] Real-Time dynamics RT_Threads=0 # [OPENMP/RT] Number of threads for real-time HXC_Potential= "IP" # [SC] SC HXC Potential % RTBands 3 | 6 | # [RT] Bands % Integrator= "RK2" # [RT] Integrator. Use keywords space separated ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA") PhLifeTime= 0.000000 fs # [RT] Dephasing Time RTstep=10.000000 as # [RT] Real Time step length NETime= 55.00000 fs # [RT] Simulation Time % IOtime 0.05 | 5.00 | 0.10 | fs # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT) % % Field1_Freq 0.00 | 0.00 | eV # [RT Field1] Frequency % Field1_Int=1.E4 kWLm2 # [RT Field1] Intensity Field1_Width= 0.000000 fs # [RT Field1] Width Field1_kind= "DELTA" # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) Field1_pol= "linear" # [RT Field1] Pol(linear|circular) % Field1_Dir 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor % % Field1_Dir_circ 0.000000 | 1.000000 | 0.000000 | # [RT Field1] Versor_circ % Field1_Tstart= 0.000000fs # [RT Field1] Initial Time
Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6, dephasing to zero and the field intensity to 1.E4.
The yambo_rt is optimized for TD-SEX (or even more sophisticated calculations). The I/O time, which is negligible in such calculations, is less optimized and becomes the most time demanding step here.
We can overcome this setting the IOtime for the polarization to 50 as (i.e. each 5 time steps).
Approach based on the Berry Phase
Use the command yambo_nl -u -F input_lr.in to generate the input:
nlinear # [R NL] Non-linear optics NL_Threads= 1 # [OPENMP/NL] Number of threads for nl-optics % NLBands 3 | 6 | # [NL] Bands % NLstep= 0.0100 fs # [NL] Real Time step length NLtime=55.000000 fs # [NL] Simulation Time NLverbosity= "high" # [NL] Verbosity level (low | high) NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.200000 | 8.000000 | eV # [NL] Energy range % NLEnSteps= 1 # [NL] Energy steps NLDamping= 0.000000 eV # [NL] Damping % ExtF_Dir 0.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor % ExtF_kind= "DELTA" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
The standard input of yambo_nl is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red.
We set the verbosity to "high" in such a way to print real-time output files.
We set the differential equation integrator to INVINT that is faster but less accurate than the default (see Ref. [1]) . This integrator is ok in case of independent particles but I advise you to use CRANKNIC integrator when correlation effects are present. Now run yambo_nl -F input_lr.in
The code will produce different files: o.polarization_F1 that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. If you plot the third column of o.polarization_F1 versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:
Results Analysis
Now we can use ypp_nl -u to analyze the results:
nonlinear # [R] NonLinear Optics Post-Processing Xorder= 1 # Max order of the response functions % TimeRange -1.000000 |-1.000000 | fs # Time-window where processing is done % ETStpsRt= 1001 # Total Energy steps % EnRngeRt 0.00000 | 10.00000 | eV # Energy range % DampMode= "LORENTZIAN" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) DampFactor= 0.10000 eV # Damping parameter
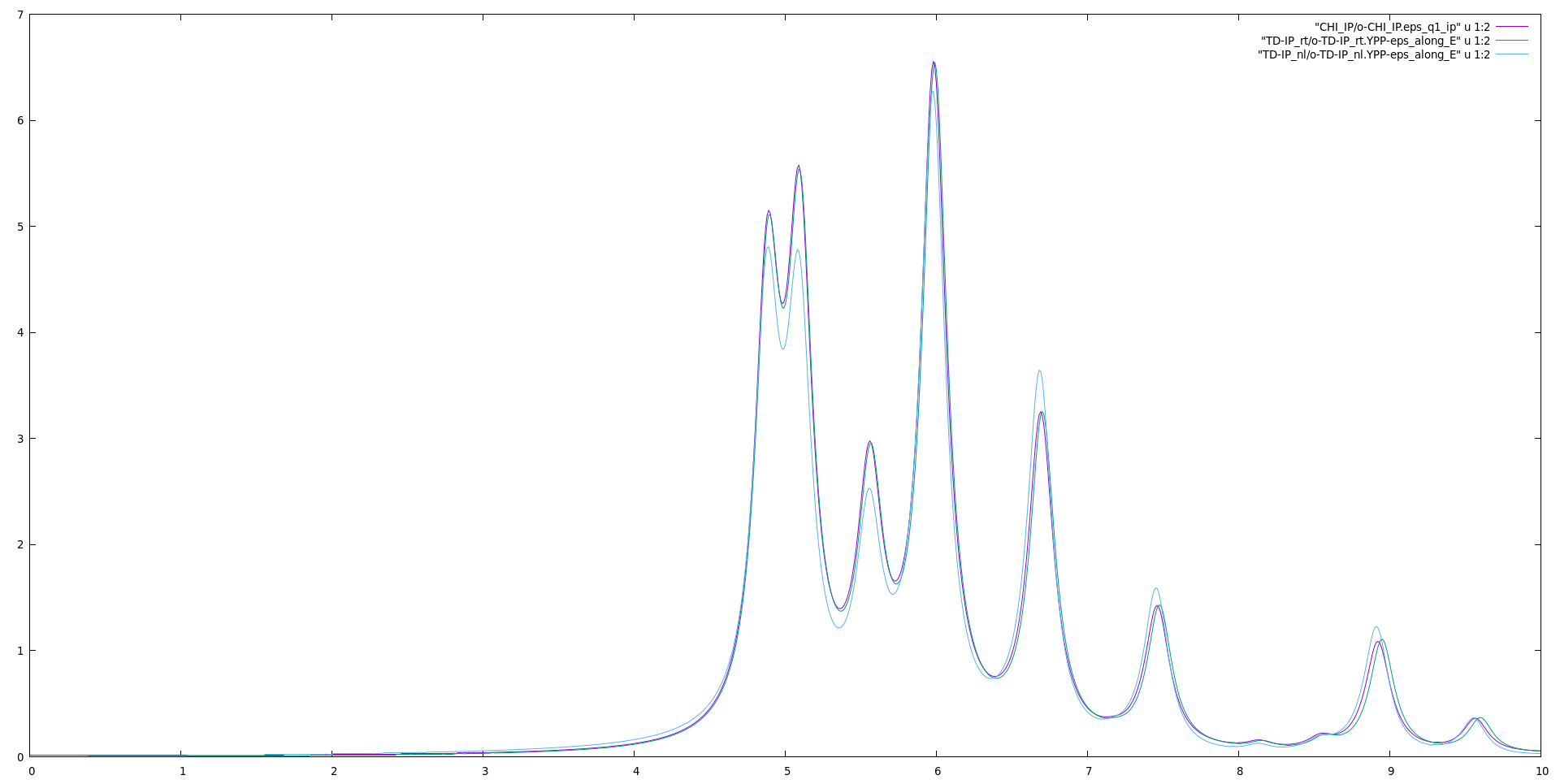
where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result. Then we run ypp_nl and obtain the following files: the dielectric constant along with the field direction o.YPP-eps_along_E, the EELS along with the same direction o.YPP-eels_along_E, and the damped polarization o.YPP-damped_polarization.
Now we can plot the dielectric constant and compare it with the linear response:
The input for the linear response can be downloaded here.
- ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)