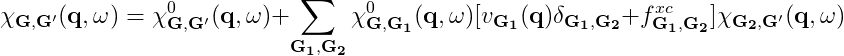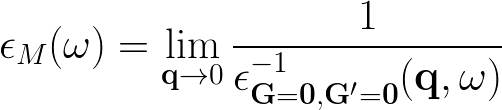Local fields: Difference between revisions
| Line 1: | Line 1: | ||
In this module you will learn how to calculate the macroscopic dielectric function in 2D hBN. | In this module you will learn how to calculate the macroscopic dielectric function in 2D hBN. | ||
== Background == | == Background == | ||
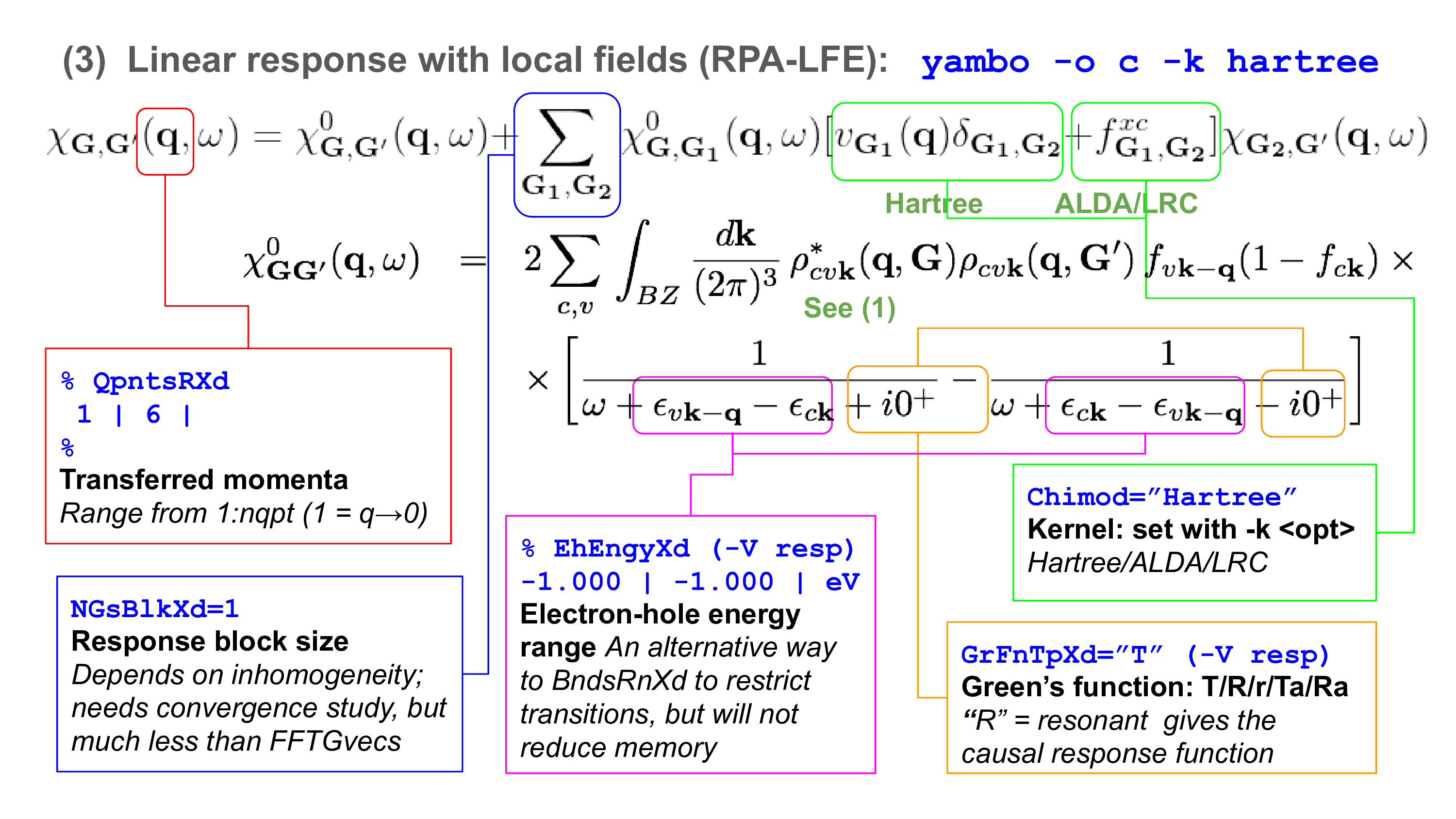
[[File:Yambo-handbook-v4.1.2-p-4.png|thumb|See the LFE cheatsheet]] | |||
The macroscopic dielectric function is obtained by including the so-called local field effects (LFE) in the calculation of the response function. Within the time-dependent DFT formalism this is achieved by solving the Dyson equation for the susceptibility ''X''. In reciprocal space this is given by: | The macroscopic dielectric function is obtained by including the so-called local field effects (LFE) in the calculation of the response function. Within the time-dependent DFT formalism this is achieved by solving the Dyson equation for the susceptibility ''X''. In reciprocal space this is given by: | ||
[[File:Yambo-CH7.png|none|x50px|Yambo tutorial image]] | [[File:Yambo-CH7.png|none|x50px|Yambo tutorial image]] | ||
Revision as of 17:39, 5 November 2019
In this module you will learn how to calculate the macroscopic dielectric function in 2D hBN.
Background
The macroscopic dielectric function is obtained by including the so-called local field effects (LFE) in the calculation of the response function. Within the time-dependent DFT formalism this is achieved by solving the Dyson equation for the susceptibility X. In reciprocal space this is given by:
The microscopic dielectric function is related to X by:
and the macroscopic dielectric function is obtained by taking the (0,0) component of the inverse microscopic one:
Experimental observables like the optical absorption and the electron energy loss can be obtained from the macroscopic dielectric function:
In the following we will neglect the f xc term: we perform the calculation at the RPA level and consider just the Hartree term (from vG) in the kernel. If we also neglect the Hartree term, we arrive back at the independent particle approximation, since there is no kernel and X = X0.
Prerequisites
- You must first complete the How to use Yambo modules
You will need:
- The
SAVEdatabases for 2D hBN - The
yamboexecutable gnuplotfor plotting spectra
Choosing input parameters
Enter the folder for 2D hBN that contains the SAVE directory, and generate the input file. From yambo -H you should understand that the correct option is yambo -o c -k hartree. Let's start by running the calculation for light polarization q in the plane of the BN sheet:
$ cd YAMBO_TUTORIALS/hBN-2D/YAMBO $ yambo (Initialization) $ yambo -F yambo.in_RPA -V RL -J q100 -o c -k hartree
We thus use a new input file yambo.in_RPA, switch on the FFTGvecs variable, and label all outputs/databases with a q100 tag. Make sure to set/modify all of the following variables to:
FFTGvecs= 6 Ry # [FFT] Plane-waves Chimod= "Hartree" # [X] IP/Hartree/ALDA/LRC/BSfxc NGsBlkXd= 3 Ry # [Xd] Response block size % QpntsRXd 1 | 1 | # [Xd] Transferred momenta % % EnRngeXd 0.00000 | 20.00000 | eV # [Xd] Energy range % % DmRngeXd 0.200000 | 0.200000 | eV # [Xd] Damping range % ETStpsXd= 2001 # [Xd] Total Energy steps % LongDrXd 1.000000 | 0.000000 | 0.000000 | # [Xd] [cc] Electric Field %
In this input file, we have:
- A q parallel to the sheet
- A wider energy range than before, and more broadening
- Selected the Hartree kernel, and expanded G-vectors in the screening up to 3 Ry (about 85 G-vectors)
LFEs in periodic direction
Now let's run the code with this new input file (CECAM in serial: about 2mins; parallel 4 tasks: 50s)
$ yambo -F yambo.in_RPA -V RL -J q100
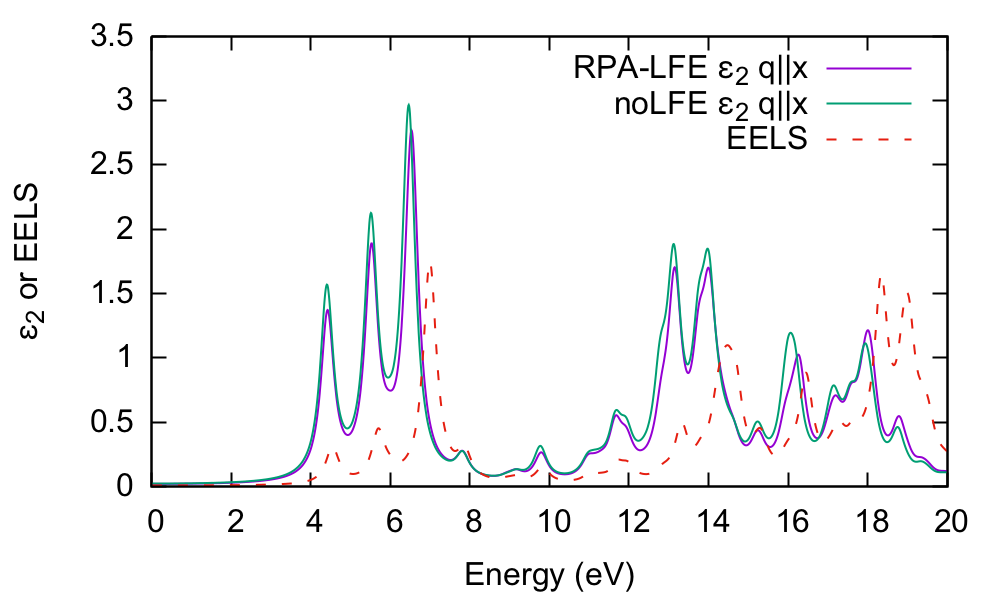
and let's compare the absorption with and without the local fields included. By inspecting the o-q100.eps_q1_inv_rpa_dyson file we find that this information is given in the 2nd and 4th columns, respectively:
$ head -n30 o-q100.eps_q1_inv_rpa_dyson # Absorption @ Q(1) [q->0 direction] : 1.0000000 0.0000000 0.0000000 # E/ev[1] EPS-Im[2] EPS-Re[3] EPSo-Im[4] EPSo-Re[5]
Plot the result:
$ gnuplot gnuplot> plot "o-q100.eps_q1_inv_rpa_dyson" u 1:2 w l,"o-q100.eps_q1_inv_rpa_dyson" u 1:4 w l
It is clear that there is little influence of local fields in this case. This is generally the case for semiconductors or materials with a smoothly varying electronic density. We have also shown the EELS spectrum (o-q100.eel_q1_inv_rpa_dyson) for comparison.
LFEs in non-periodic direction
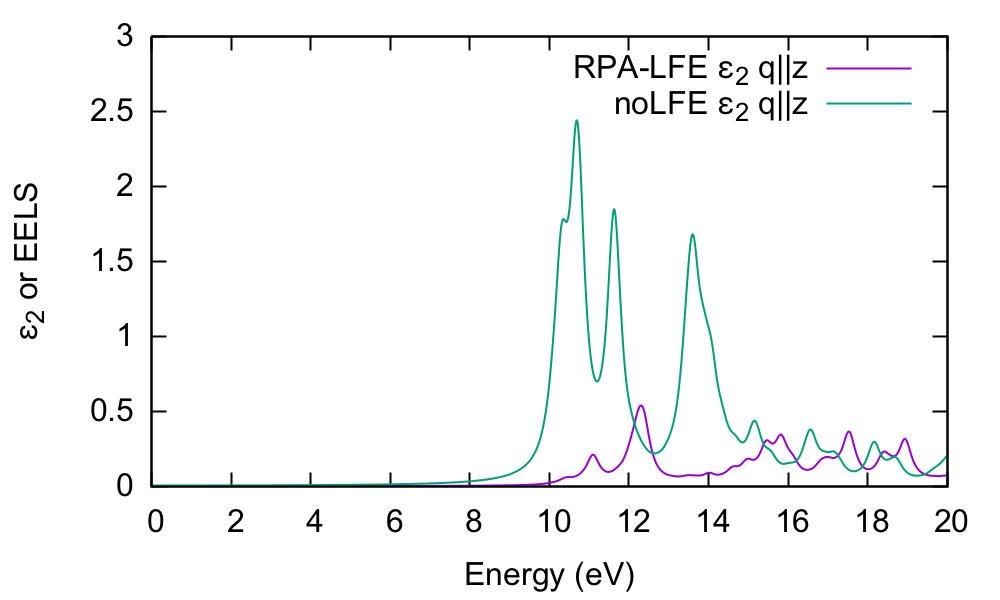
Now let's switch to q perpendicular to the BN plane:
$ yambo -F yambo.in_RPA -V RL -o c -k hartree and set ... % LongDrXd 0.000000 | 0.000000 | 1.000000 | # [Xd] [cc] Electric Field %
You can try out the default parallel usage now, or run again in serial, i.e.
$ yambo -F yambo.in_RPA -V RL -J q001 (serial) $ mpirun -np 4 yambo -F yambo.in_RPA -V RL -J q001 & (parallel, MPI only, 4 tasks)
As noted previously, the log files in parallel appear in the LOG folder, you can follow the execution with tail -F LOG/l-q001_optics_chi_CPU_1 .
Plotting the output file:
$ gnuplot gnuplot> plot "o-q001.eps_q1_inv_rpa_dyson" u 1:2 w l,"o-q001.eps_q1_inv_rpa_dyson" u 1:4 w l
In this case, the absorption is strongly blueshifted with respect to the in-plane absorption. Furthermore, the influence of local fields is striking, and quenches the spectrum strongly. This is the well known depolarization effect. Local field effects are much stronger in the perpendicular direction because the charge inhomogeneity is dramatic. Many G-vectors are needed to account for the sharp change in the potential across the BN-vacuum interface.
Absorption versus EELS
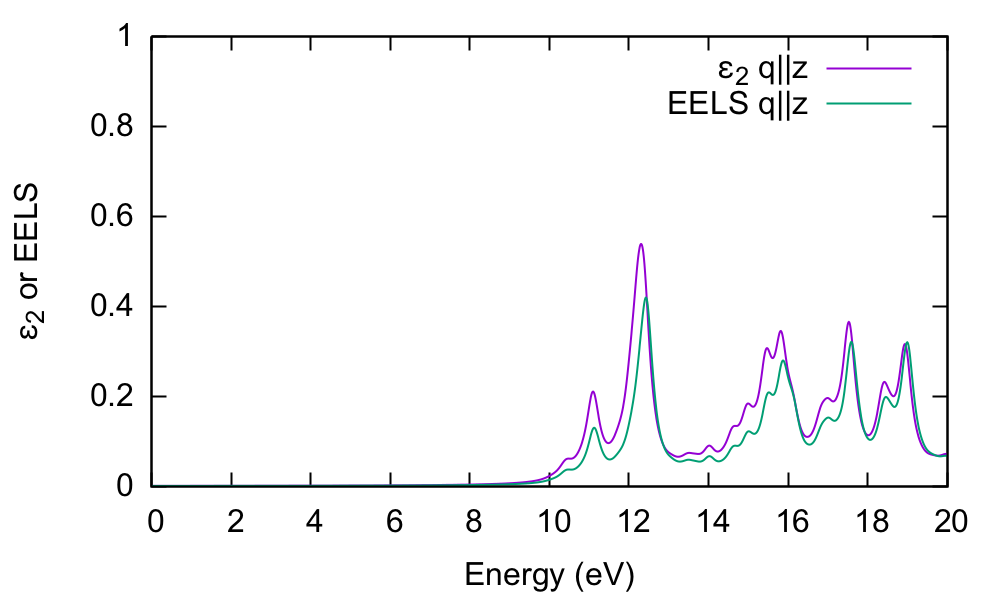
In order to understand this further, we plot the electron energy loss spectrum for this component and compare with the absorption:
$ gnuplot gnuplot > plot "o-q001.eps_q1_inv_rpa_dyson" w l,"o-q001.eel_q1_inv_rpa_dyson" w l
The conclusion is that the absorption and EELS coincide for isolated systems. To understand why this is, you need to consider the role of the macroscopic screening in the response function and the long-range part of the Coulomb potential. See e.g.[1]
Summary
From this tutorial you've learned:
- How to compute the macroscopic dielectric function by solving the Dyson equation for X in G-space
- The connection between absorption and EELS in low-dimensional systems
| Prev: Back to First steps | Now: Tutorials Home --> First steps --> 2D hBN --> RPA with Local Fields | Next: Back to First steps |
- ↑ TDDFT from molecules to solids: The role of long‐range interactions, F. Sottile et al, International journal of quantum chemistry 102 (5), 684-701 (2005)