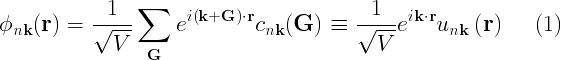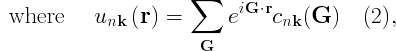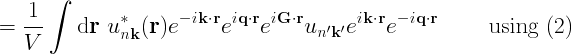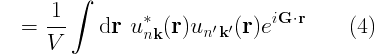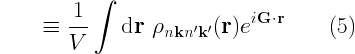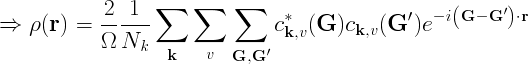The Fast Fourier Transformation

Fast Fourier Transformation (FFT)

The Fast Fourier transform (FFT) is an efficient algorithm for computing the discrete Fourier transform and its inverse. In the mathematics and engineering fields, the FFT is frequently used to transform between the frequency and time domains. In plane-wave codes such as yambo, the 3-dimensional complex-complex FFT algorithm is very heavily used to transform functions (typically wavefunctions or densities) from real space (r,R) into their counterparts in reciprocal space (k,q,G), and back again via the inverse transform. Since wavefunctions and densities are sampled on finite grids based on the reciprocal lattice vectors (G), e.g.

a discrete Fourier transform is necessary to transform them to finite grids in the unit cell. Likewise, integrals are transformed into weighted sums.

Implementation

Calls to FFT routines can be found in yambo in several places, for instance during the computation of optical oscillators (see Dynamical Response ) or the exchange self-energy (see Hartree-Fock ), or in loading the wavefunctions (see src/2wf_and_fft/wfload.F). In the first two cases the quantity of interest (matrix element) has the form

This quantity could be computed by expanding the wavefunctions in G space using (1), and carrying out various sums and integrals- including a double sum over G! However, the matrix element can also be computed using a Fourier transform:

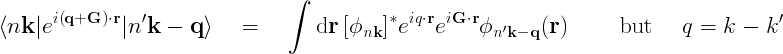
However, this is just the Fourier transform of

In practice, the real space integral could be discretized over N_R points, and converted into a sum; the Fourier transforms are hence discrete. Therefore, we note that the matrix element (3) can be calculated by:

1. Converting both wavefunctions to the same real space grid, by means of FTs (see (2));
2. Computing the simple product of the wavefunctions in real space, to obtain the product appearing inside (4);
3. Carrying out the (inverse) FT (i.e., compute (4)), to obtain (6).

Why bother doing all this? Because it turns out that the FT can be carried out very efficiently, and is much faster than doing the products of the wavefunctions in reciprocal space!

Efficiency

We can illustrate the efficiency of the FFT by considering a more simple example: calculation of the density in real space:

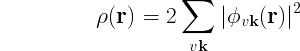
Number of computations in reciprocal space method:

However, if we transform the wavefunctions to real space first using the Fast Fourier Transform routine (i.e., NOT just by regularly calculating the sum over G, as in the usual discrete Fourier transform):

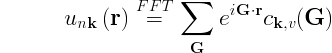
where the expression on the left is evaluated using a call to the FFT routine, we can then obtain

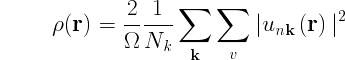
Number of computations in real space/FFT method:

If you really want to find out why an FFT is faster than a regular FT, you can find further information in the references. Most people just treat FFT routines as black boxes, and this includes the good people of yambo. To summarise: the number of computations required for an N-point discrete Fourier Transform is 2N² if a straightforward algorithm is used. An FFT algorithm reduces this to 2 N ln(N). Since calls to the FFT routine constitute a large part of the total runtime, it is important to have highly efficient FFT libraries (and if possible, tuned to the hardware). Presently, yambo has the possibility of using the routines of Stefan Goedecker (hardwired internally: src/2wf_and_fft/sgfft.F) or the FFTW routines (external libraries, set FFTW_LIBS when configuring). Other efficient vendor specific libraries are included in the IBM ESSL, the AMD ACML and the Intel MKL libraries, although these are not coded into yambo as yet.

Numerical factors: grids and cutoffs

This brings us to one of the most important tuning parameters in yambo: FFTGvecs . This determines the number of G-vectors used in the FFT routine. It is strongly advised that you test the convergence of your spectrum with this parameter! Usually you will find you can reduce the calculation time by a considerable amount by reducing this factor from the default (the number of G's in the DFT wavefunctions), without affecting the accuracy much. Note that this applies also to the calculation of the optical oscillators (q->0; G,G'=0), where the FFT routine is not actually used.

References

• S. Goedecker, Rotating a three-dimensional array in optimal positions for vector processing: Case study for a three-dimensional Fast Fourier Transform, Comp. Phys. Commun. 76, 294 (1993)
• FFTW: The fastest Fourier Transform in the West, http://www.fftw.org
• FFT theory at Wikipedia
• FFT theory at Mathworld