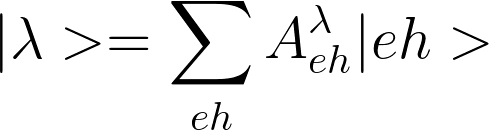How to analyse excitons

In this tutorial you will learn (for a 2D-hBN) how to:

• How to analyze a BSE optical spectrum in terms of excitonic eigenvectors and eigenvalues
• How to plot the excitonic wavefunction

Prerequisites

Previous modules

• You must have completed the tutorial on 2D hBN.
• You must have completed the tutorial on 2D hBN.

You will need:

• ypp executable
• xcrysden executable
• gnuplot or xmgrace executable

YAMBO calculations

If you have completed the tutorials of 2D hBN you should have all the databases required to do this tutorial in your SAVE and 2D directories

$ ls ./SAVE
ndb.gops			ns.kb_pp_pwscf_fragment_2	ns.kb_pp_pwscf_fragment_7	ns.wf_fragments_4_1
ndb.kindx			ns.kb_pp_pwscf_fragment_3	ns.wf				ns.wf_fragments_5_1
ns.db1				ns.kb_pp_pwscf_fragment_4	ns.wf_fragments_1_1		ns.wf_fragments_6_1
ns.kb_pp_pwscf			ns.kb_pp_pwscf_fragment_5	ns.wf_fragments_2_1		ns.wf_fragments_7_1
ns.kb_pp_pwscf_fragment_1	ns.kb_pp_pwscf_fragment_6	ns.wf_fragments_3_1
$ ls ./2D
ndb.BS_Q1_CPU_0			ndb.dip_iR_and_P		ndb.dip_iR_and_P_fragment_6	ndb.pp_fragment_4
ndb.BS_diago_Q01		ndb.dip_iR_and_P_fragment_1	ndb.dip_iR_and_P_fragment_7	ndb.pp_fragment_5
ndb.HF_and_locXC		ndb.dip_iR_and_P_fragment_2	ndb.pp				ndb.pp_fragment_6
ndb.QP				ndb.dip_iR_and_P_fragment_3	ndb.pp_fragment_1		ndb.pp_fragment_7
ndb.RIM				ndb.dip_iR_and_P_fragment_4	ndb.pp_fragment_2
ndb.cutoff			ndb.dip_iR_and_P_fragment_5	ndb.pp_fragment_3

Sorting the excitonic eigenvalues

$ ypp -e -s -J 2D 

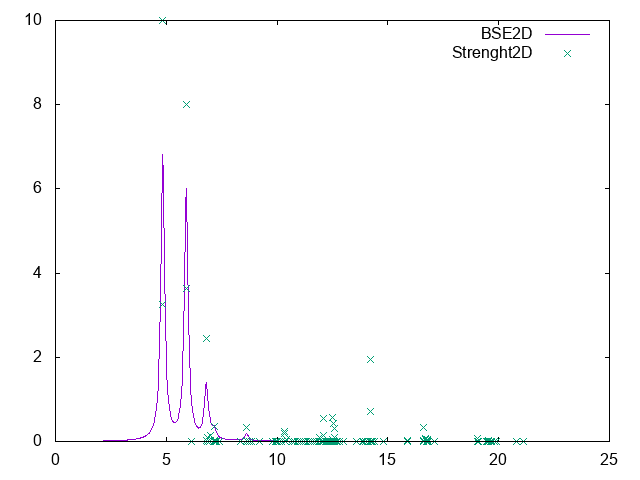
The new generated file o-2D.exc_E_sorted (o-2D.exc_E_sorted) reports the energies of the excitons and their Dipole Oscillator Strenghts sorted by energy (Index).

Open the first file and look inside. The first exciton is at 4.83 eV and the second one has the highest strenght (normalized to 1) Attention: clearly the convergence of these results has to be checked doing several BSE calculations with different k-grids!

Or you can make a plot

$ gnuplot
gnuplot> plot 'o-2D.eps_q1_diago_bse' w l title 'BSE2D' ,'o-2D.exc_E_sorted' u 1:($2*10) title 'Strenght2D'

Analyze the excitons

We can now analyze the excitons in terms of single-particle states to do that create the appropriate input

$ ypp -e a -F ypp.AMPL.in -J 2D

To analyze the first 5 excitons change this line as:

States= "1 - 5"              # Index of the BS state(s)

Close the input and run ypp

$ ypp -J 2D -F ypp_AMPL.in

$ls ls o*exc*at*
o-2D.exc_amplitude_at_1	o-2D.exc_amplitude_at_3	o-2D.exc_amplitude_at_5	o-2D.exc_weights_at_2	o-2D.exc_weights_at_4
o-2D.exc_amplitude_at_2	o-2D.exc_amplitude_at_4	o-2D.exc_weights_at_1	o-2D.exc_weights_at_3	o-2D.exc_weights_at_5

Open the files for the first exciton o-2D.exc_weights_at_1 reports the Weights, while o-2D.exc_weights_at_1 the amplitudes

where given the exciton in terms of e,h states, the weights are while the amplitudes are defined as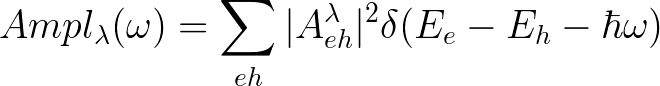

weights [math]\displaystyle{ |\Lambda_{eh}^\lambda|^2 }[/math] where