Nonequilibrium absorption in bulk silicon: Difference between revisions
Petru Milev (talk | contribs) |
Petru Milev (talk | contribs) |
||
| Line 142: | Line 142: | ||
</div> | </div> | ||
Where <code>BSEBands</code> was changed to include bands from 3 to 8, which defines the basis of quasiparticle pairs that are used to describe excitons. 2 valence and 4 conduction bands where included. <code>BEnRange</code> was increased to from 0-10 eV to 0-16 eV, and <code>BEnSteps</code> was increased from 100 to 200. The scissors operator <KfnQP_E> was used to match the positon calculated spectra with experimental values. | Where <code>BSEBands</code> was changed to include bands from 3 to 8, which defines the basis of quasiparticle pairs that are used to describe excitons. 2 valence and 4 conduction bands where included. <code>BEnRange</code> was increased to from 0-10 eV to 0-16 eV, and <code>BEnSteps</code> was increased from 100 to 200. The scissors operator <code>KfnQP_E</code> was used to match the positon calculated spectra with experimental values. | ||
To run the file: | To run the file: | ||
Revision as of 19:18, 15 November 2024
In this tutorial you will learn the basic concepts for computing changes in the optical properties of a semi-conductor in presence of a non-equilibrium electrons and holes distribution in conduction and valence band respectively. This tutorial is based on the results published in Phys. Rev. B[1]
Under construction
The material: Silicon
We will study nonequilibrium absorption in bulk silicon. The same material used for this [Silicon|GW tutorial]
- FCC lattice
- Two atoms per cell (8 electrons)
- Lattice constant 10.183 [a.u.]
- Plane waves cutoff 15 Rydberg
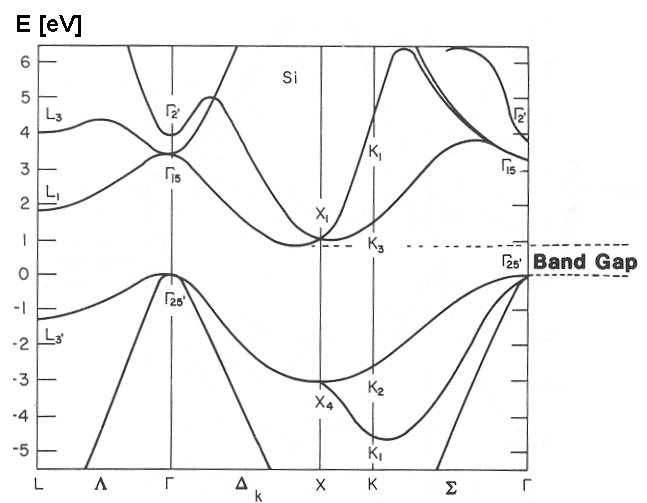
- Direct gap 3.4 eV at Gamma
- Indirect gap 1.1 eV between Gamma= (0 0 0) and a point X', close to X=(0 1 0)
Tutorial files and Tutorial structure
Follow the instructions in Tutorials#Files and download/unpack the Silicon.tar.gz.
Once the tutorial archive file is unzipped the following folder structure will appear
COPYING README Silicon/
with the Solid_Si folder containing
> ls Silicon/ PWSCF/ YAMBO/
In the Pwscf folder the student will find an input/output directory with input/output files for pw.x. The Silicon pseudopotential file is also provided.
> ls PWSCF/ convergence_scripts input output psps
In the convergence_scripts you will find some useful shell scripts to run the ground state convergence runs for Silicon.
The YAMBO folder contains the Yambo input/output files and core databases.
> ls YAMBO/ 2x2x2/ 4x4x4/ 6x6x6/ 8x8x8/ Convergence_Plots_and_Scripts/ GAMMA/
The core databases are provided for several k-points grids. In addition the folder Convergence_Plots_and_Scripts contains some scripts used for the [Silicon|GW tutorial] .
Here we will just use the 8x8x8 (which is still very far from convergence) folder for computing (nonequilibrium) optical properties.
To run the tutorial you will need the standard executables
yambo ypp
plus the executables of the real time module of the Yambo code
yambo_rt ypp_rt
Equilibrium optical properties
We start from a density-functional theory (DFT) calculation. Then we apply MBPT to obtain the QP energies within the GW approximation and the absorption spectra from the solution of the BSE. The QP band structure will show the effect of the screened electron-electron interaction, while the absorption spectrum within the BSE accounts for the effect of the electron-hole interaction. When QP corrections are not available, they can be included using the scissor operator KfnQP_E, and the numerical values for "corrections" can be deduced from a GW calculation. For more information about solving the Equilibrium BSE equation refer to the following tutorial: Calculating optical spectra including excitonic effects: a step-by-step guide
(to delete open) In this case, do we actually compute the qp eng withing gw approximation? or we directy solve the bse eq (to delete close)
Enter the folder 8x8x8, and initialize yambo in the respective folder
$ cd 8x8x8 $ yambo
For this step you can either compute static screening at equilibrium, or use the screening computed for the GW step in the Bethe-Salpeter.
Static screening at equilibrium
First, to solve the BSE equation we need to calculate the statically screened electron-electron interaction (W), which is related to static diaelectric screening [math]\displaystyle{ \epsilon^{-1} }[/math].
[math]\displaystyle{ \Large \epsilon^{-1}_{\mathbf{G},\mathbf{G'}} (\mathbf{q}, \omega = 0) = \delta_{\mathbf{G},\mathbf{G'}} + v(\mathbf{v} + \mathbf{G}) \chi_{\mathbf{G},\mathbf{G'}(\mathbf{q}}, \omega = 0) }[/math]
To do this create the following input file:
$ yambo -X s -F 01_EQ_BSE_screening.in
with the following contents:
em1s # [R][Xs] Statically Screened Interaction % BndsRnXs 1 | 30 | # [Xs] Polarization function bands % NGsBlkXs= 3 Ry # [Xs] Response block size % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field %
Where we changed the response block size NGsBlkXs = 3 Ry and number of polarization function bands BndsRnXs to be in the range of 1 to 30. Now run the file:
$ yambo -F 01_EQ_BSE_screening.in -J EQ_BSE
Solving the Bethe-Salpeter equation
To solve the Bethe-Salpeter equation, the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. For a non spin-polarized system and in the [math]\displaystyle{ q = 0 }[/math] limit, the two-particle Hamiltonian matrix elements are given by
[math]\displaystyle{ \Large H_{vc\mathbf{k},v'c'\mathbf{k'}} = (\varepsilon_{c\mathbf{k}} - \varepsilon_{v\mathbf{k}})\delta_{vv'}\delta_{cc'}\delta_{\mathbf{k},\mathbf{k'}} + (f_{c\mathbf{k}} - f_{v\mathbf{k}})\left[ 2V_{vc\mathbf{k},v'c'\mathbf{k'}} - W_{vc\mathbf{k},v'c'\mathbf{k'}}\right] }[/math]
where [math]\displaystyle{ vc\mathbf{k} }[/math] indicates the pair of quasiparticle states [math]\displaystyle{ v\mathbf{k} }[/math] and [math]\displaystyle{ c\mathbf{k} }[/math]. The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part V (which stems from the Hartree potential) and the electron-hole attraction part W (which stems from the screened exchange potential). The electron-hole attraction part W, depends on [math]\displaystyle{ \epsilon^{-1} }[/math] which was calculated in the previous section.
After calculating the equilibrium Bethe-Salpeter kernel, the resulting two-particle Hamiltonian can be diagonalized to compute the macroscopic dielectric function, which can be used to get absorption and EELS spectra. Calculation of BS kernel and diagonalization of Hamiltonian can be done in one step.
To generate the input file for the calculation of BSE kernel, run the following command:
$ yambo -o b -k sex -F 02_EQ_BSE_kernel_diag.in -y d -J EQ_BSE
with the following input
optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. K_Threads=0 # [OPENMP/BSK] Number of threads for response functions BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 2085 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] % BSEQptR 1 | 1 | # [BSK] Transferred momenta range % % BSEBands 3 | 8 | # [BSK] Bands range % % BEnRange 2.00000 | 15.00000 | eV # [BSS] Energy range % % KfnQP_E 5.80000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) % % BDmRange 0.100000 | 0.100000 | eV # [BSS] Damping range % BEnSteps= 200 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field versor % BSEprop= "abs" # [BSS] Can be any among abs/jdos/kerr/asymm/anHAll/magn/dich/photolum/esrt BSEdips= "none" # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane
Where BSEBands was changed to include bands from 3 to 8, which defines the basis of quasiparticle pairs that are used to describe excitons. 2 valence and 4 conduction bands where included. BEnRange was increased to from 0-10 eV to 0-16 eV, and BEnSteps was increased from 100 to 200. The scissors operator KfnQP_E was used to match the positon calculated spectra with experimental values.
To run the file:
$ yambo -F 02_EQ_BSE_kernel_diag.in -J EQ_BSE
Generating non-equilibrium carriers
Energy shift in the band structure
The GW method is the standard approach to compute quasi-particle corrections. However, in presence of non-equilibrium carriers, or even at finite temperature the formulation of the GW self-energy needs to be refined. This is due to its frequency dependence, which results in extra terms when performing the analytic continuation from the Keldish contour (non-equilibrium case) or from the Matsubara axis (finite temperature case) to the real time/frequency axis. See for example this reference [2] for the finite temperature case. On the other hand the COHSEX self-energy, being static, avoids this complication. This is why we will compute changes in the QP corrections within the COHSEX approximation.
COHSEX corrections at equilibrium
Screening in presence of non-equilibrium carriers
COHSEX corrections in presence of non-equilibrium carriers
Renormalization of the exciton binding energy
We finally perform a BSE calculation loading both the nonequilibrium carriers and the quasi-particle energy shifts.