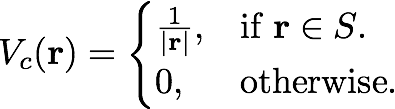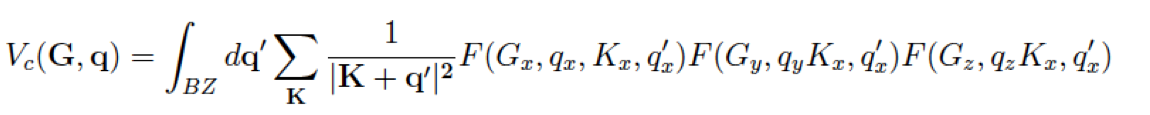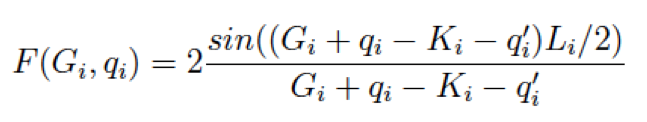How to treat low dimensional systems

In this tutorial you will learn (for a 2D material) how to:

• generate a coulomb potential with a box-like cutoff in the non-periodic direction
• visualize this coulomb potential
• use this cutoff in the HF, GW and BSE calculation
• analyze the difference with similar calculations without cutoff

Prerequisites

• Complete the Generating the Yambo databases tutorial
• SAVE folder for 2D hBN.
• yambo executable
• ypp executable
• Run Initialization

Generate the cutoff database (yambo -r)

To simulate a real isolated 2D-material a convergence with vacuum size is in principle required. but the use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images. (see ref. Varsano)

The cutoff

For a 2D system a box-like cutoff in the direction perperdicular to the sheet (in this case z) is applied. The used box size L_z = a_z (cell size in bohr) - 1 bohr = 32 bohr

Create the input file:

$ yambo -F 01_cut2D.in  -r

Open the input file 01_cut2D.in

Change the variables inside as:

RandQpts= 1000000          # [RIM] Number of random q-points in the BZ
RandGvec= 100        RL    # [RIM] Coulomb interaction RS components

CUTGeo= "box z"            # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY..
% CUTBox
 0.00     | 0.00     | 32.0    |        # [CUT] [au] Box sides

Close the input file and run yambo

$ yambo -F 01_cut2D.in  -J 2D