Yambopy tutorial: band structures: Difference between revisions
| Line 79: | Line 79: | ||
xml.plot_eigen(path_kpoints) | xml.plot_eigen(path_kpoints) | ||
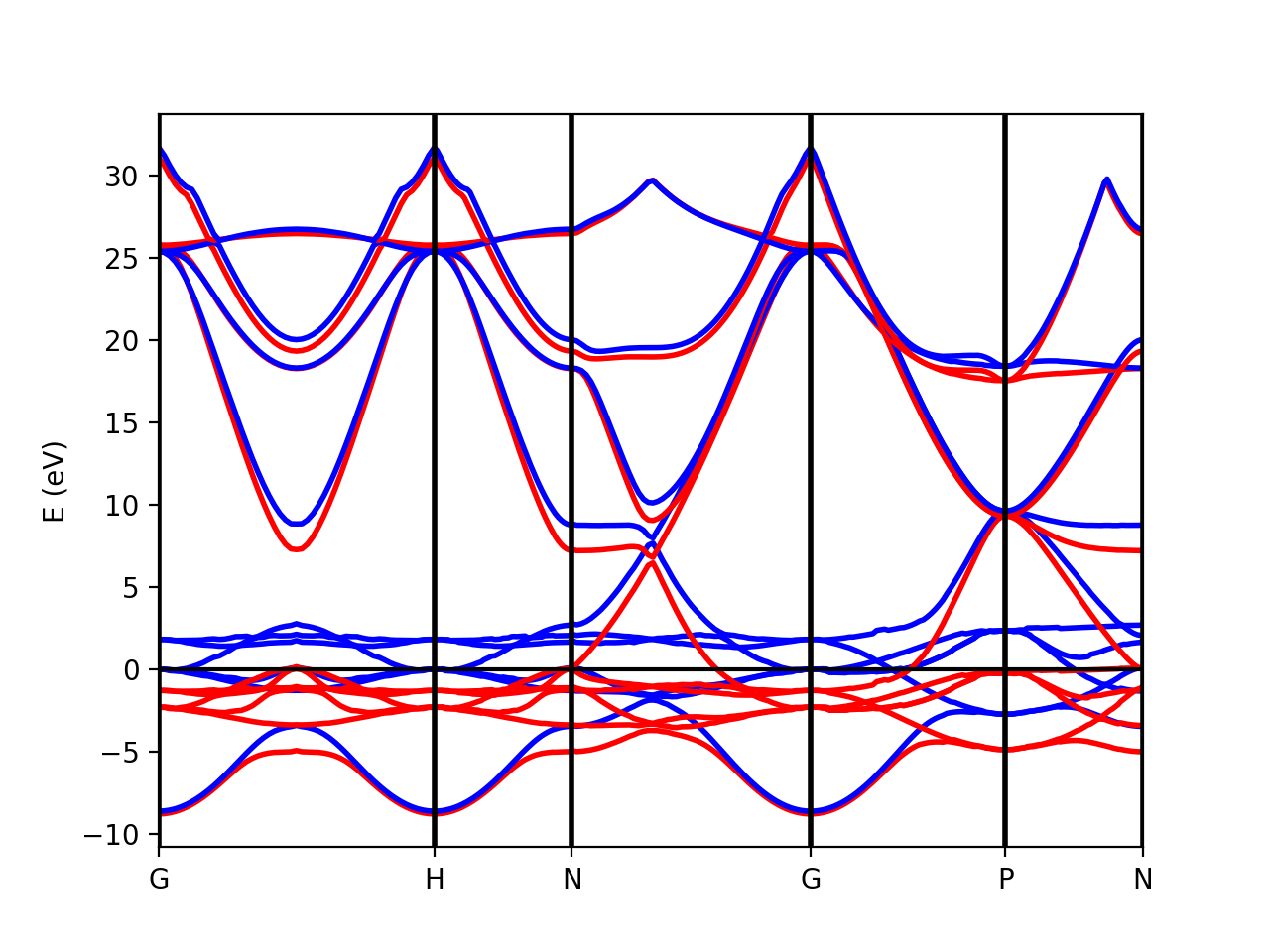
[[File:Figure 3-iron-bands.png| | [[File:Figure 3-iron-bands.png| 600 px | center |Spin polarized band structure of iron calculated by DFT]] | ||
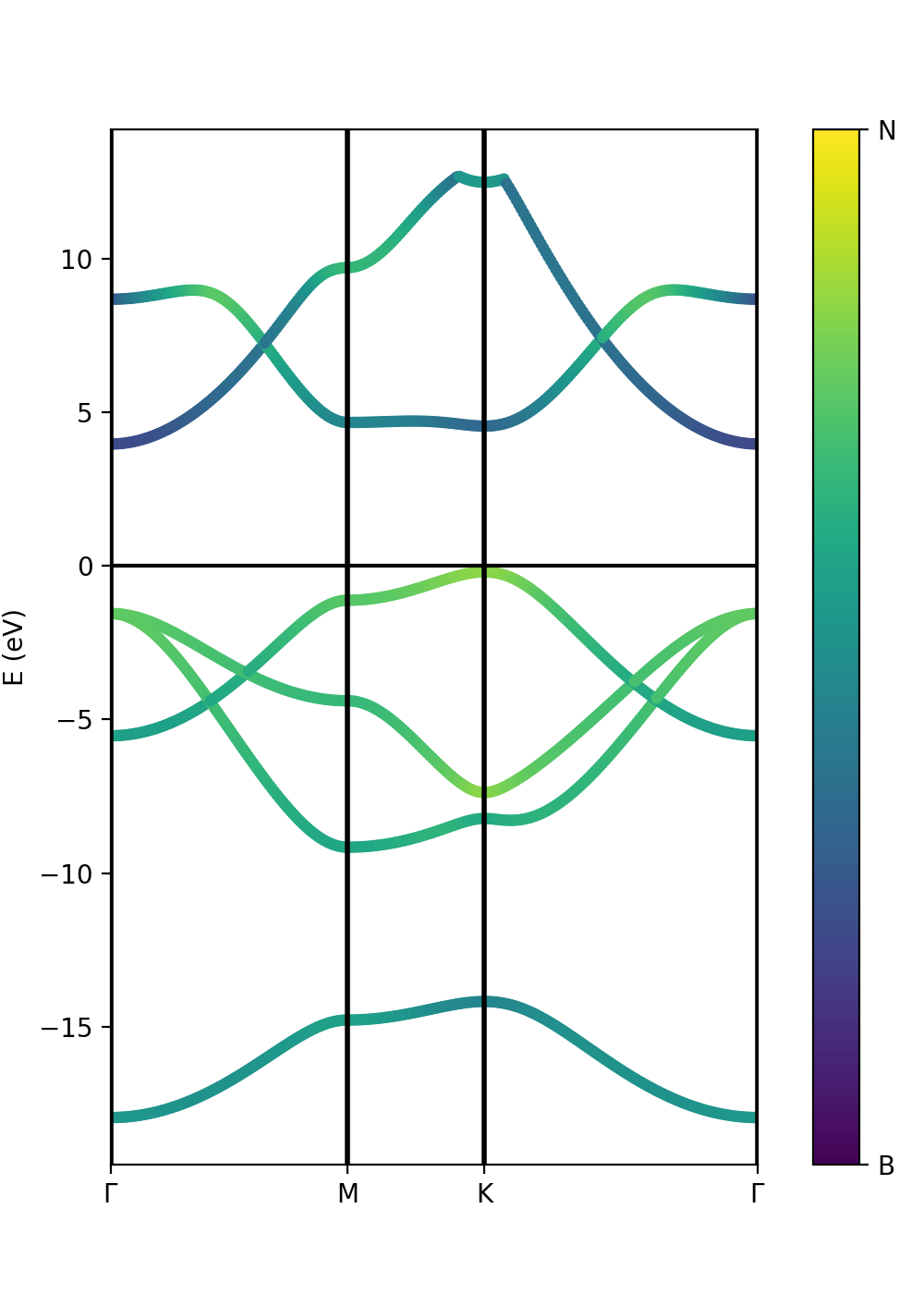
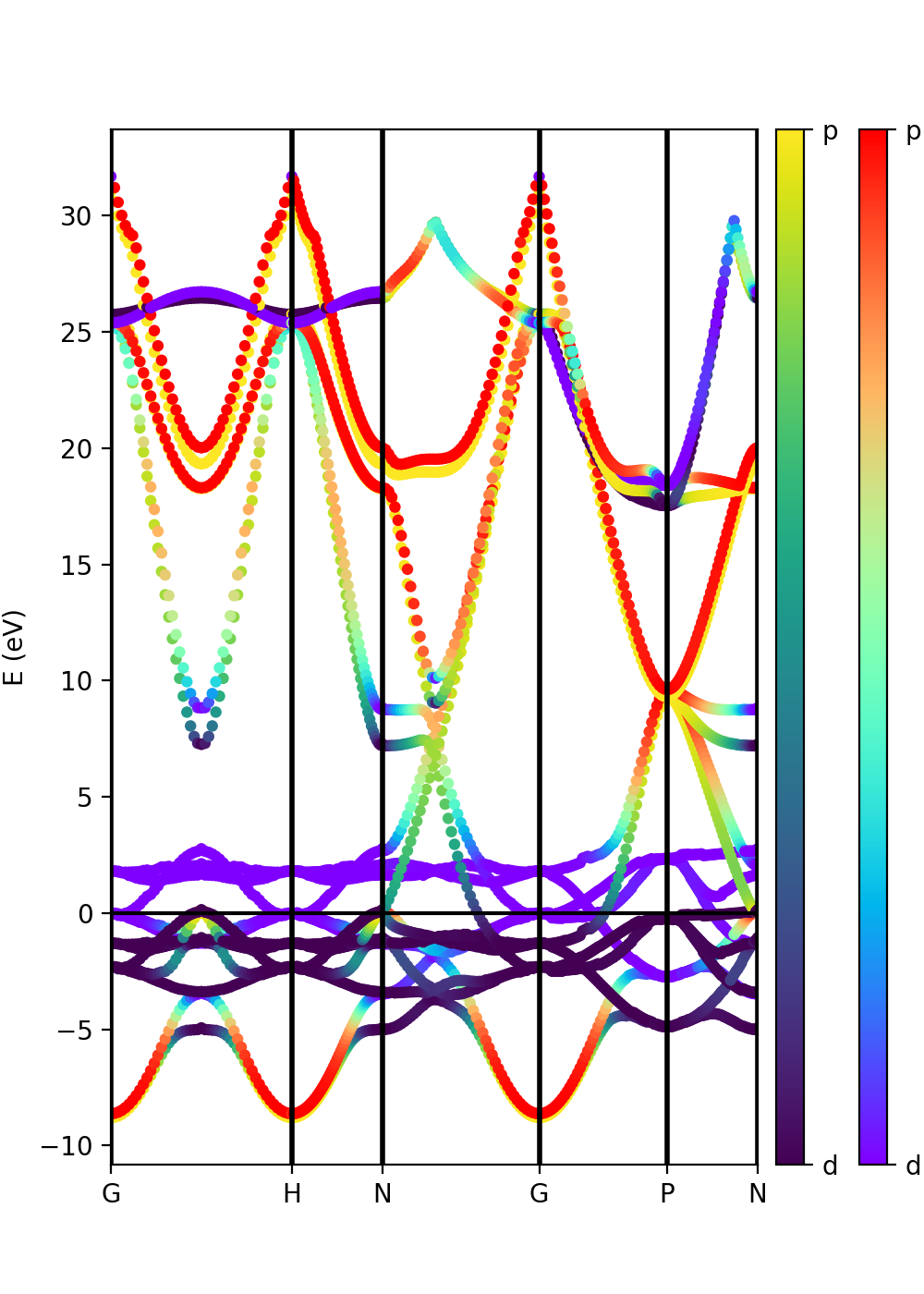
[[File:Figure 4-iron-bands-size-d-orbitals.png|400px|center|Iron band structure. Size is proportional to the weights of the projection on atomic d-orbitals. Red (blue) is up (down) spin polarization.]] | [[File:Figure 4-iron-bands-size-d-orbitals.png|400px|center|Iron band structure. Size is proportional to the weights of the projection on atomic d-orbitals. Red (blue) is up (down) spin polarization.]] | ||
Revision as of 15:25, 4 April 2022
The full tutorial, including the Quantum espresso and Yambo databases that we will read, can be downloaded and extracted from the yambo website:
$wget www.yambo-code.org/educational/tutorials/files/databases_qepy.tar $tar -xvf databases_qepy.tar $cd databases_qepy
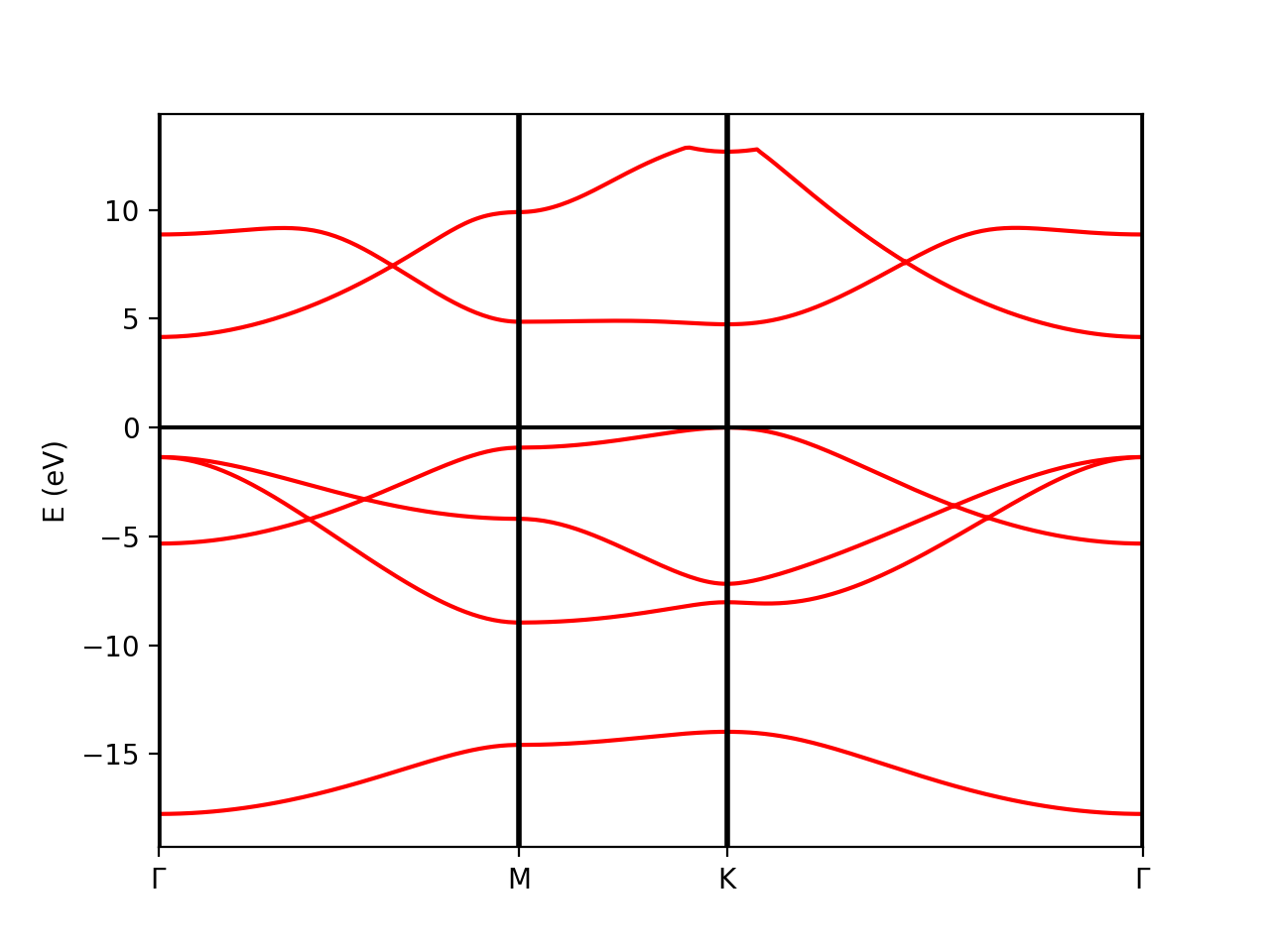
Tutorial 1. BN (semiconductor). Band structure
The qepy classes are useful not only to execute Quantum Espresso but also to analyze the results. The full qepy library is imported by simply doing:
from qepy import *
Plot Band structure
The class PwXML reads the data file generated by Quantum Espresso and post-process the data. The class is initiated doing:
xml = PwXML(prefix='bn', path='bands')
The variable prefix corresponds to the same variable of the QE input. The folder location is indicated by variable path. Previously to plot the bands, we define the k-points path using the function Path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0],'$\Gamma$'],
[[0.5, 0.0, 0.0],'M'],
[[1./3,1./3,0.0],'K'],
[[0.0, 0.0, 0.0],'$\Gamma$']], [int(npoints*2),int(npoints),int(sqrt(5)*npoints)])
It is worth to note that the path should coincide with the selected path for the QE calculations.
In order to plot we do:
xml.plot_eigen(path_kpoints)
This function will automaticall plot the bands as shown below.
Alternatively we can use the function plot_eigen_ax. This functions requires as input the figure object and with given axes, as in the next example.
Plot atomic orbital projected Band structure
In addition to the band structure, useful information regarding the atomic orbital nature of the electronic bands can be displayed using the class ProjwfcXML. Before we need to use the QE function projwfc.x to create the file atomic_proj.xml. The function projects wavefunctions onto orthogonalized atomic wavefunctions, among others functionalities. The orbital order is explained in the input documentation of the projwfc.x function (https://www.quantum-espresso.org/Doc/INPUT_PROJWFC.html#idm94). To run projwf.x we can use the class ProjwfcIn:
proj = ProjwfcIn(prefix='bn') proj.run(folder='bands')
Be aware that this can take a while in a large system with many k-points. As in the class PwXML, we define the path_kpoints and also the selected atomic orbitals to project our bands. We have chosen to represent the projection weight onto the boron and nitrogen orbitals
atom_1 = list(range(16)) atom_2 = list(range(16,32))
The full list of orbitals is written in the file bands/prowfc.log. We have also defined the figure box
import matplotlib.pyplot as plt fig = plt.figure(figsize=(5,7)) ax = fig.add_axes( [ 0.12, 0.10, 0.70, 0.80 ])
The class ProjwfcXML runs with this example:
band = ProjwfcXML(prefix='bn',path='bands',qe_version='7.0') band.plot_eigen(ax,path_kpoints=path_kpoints,cmap='viridis',selected_orbitals=atom_1,selected_orbitals_2=atom_2)
We have chosen the colormap 'viridis' (variable cmap). We can also plot the bands varying the size. In this case we pass only the variable selected_orbitals (see next tutorial).
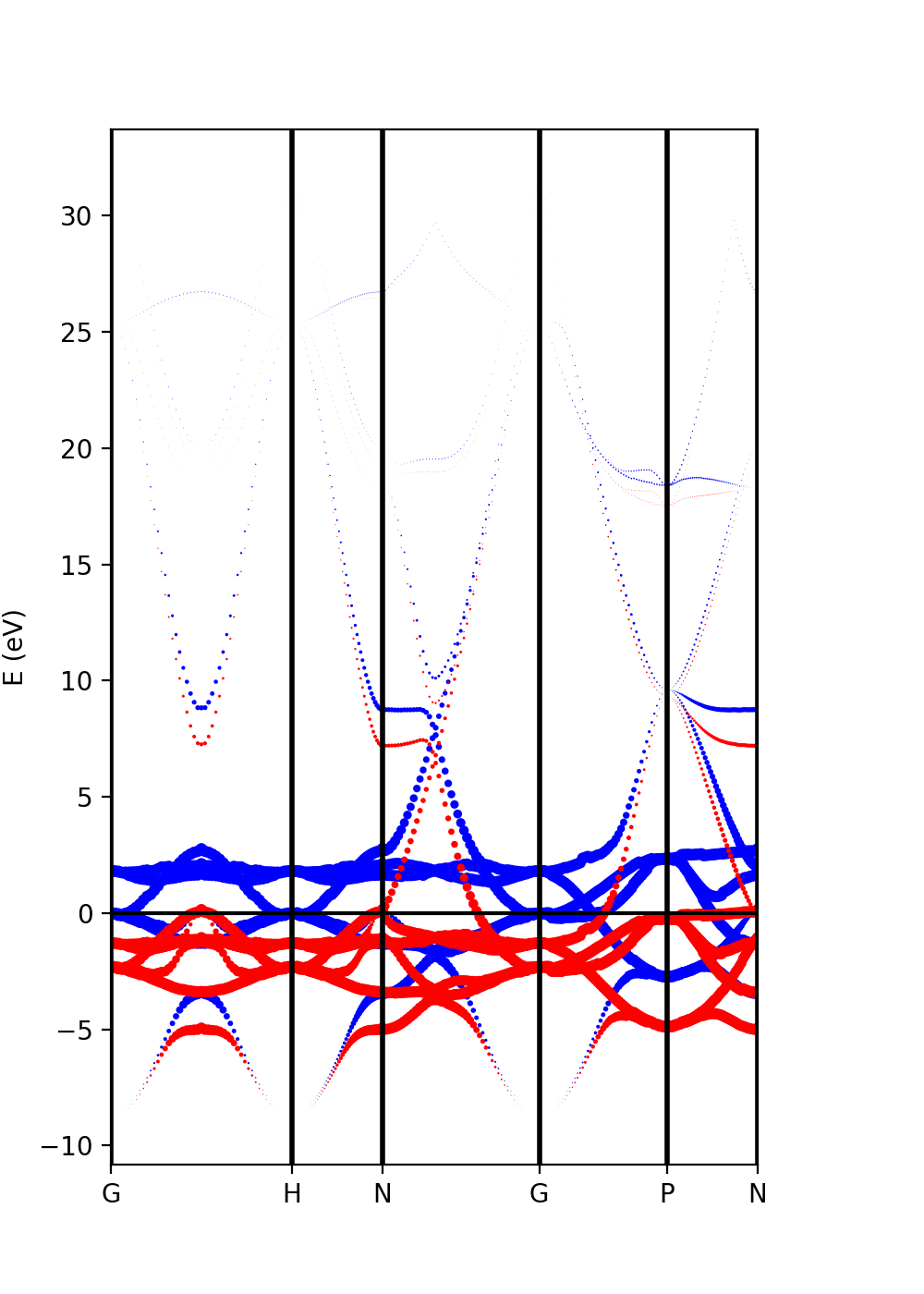
Tutorial 2. Iron. Ferromagnetic metalic material
In the case of spin-polarized calculations we can plot the spin up and down band structures. The class PwXML automatically detects the spin polarized case (nspin=2 in QE input file). The spin up channel is displayed with red and the spin down channel with blue. In the case of iron we have selected this path:
npoints = 50
path_kpoints = Path([ [[0.0, 0.0, 0.0 ],'G'],
[[0.0, 0.0, 1.0 ],'H'],
[[1./2,0.0,1./2.],'N'],
[[0.0, 0.0, 0.0 ],'G'],
[[1./2, 1./2, 1./2 ],'P'],
[[1./2,0.0,1./2. ],'N']], [npoints,npoints,npoints,npoints,npoints])
xml = PwXML(prefix='pw',path='bands/t0') xml.plot_eigen(path_kpoints)
Tutorial 3
Links
- Back to ICTP 2022#Tutorials