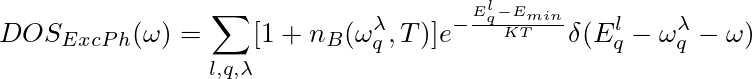Optical properties at finite temperature: Difference between revisions
No edit summary |
|||
| Line 45: | Line 45: | ||
The temperature effect is clearly visible in the figure. | The temperature effect is clearly visible in the figure. | ||
== Bethe-Salpeter at finite temperature == | == Bethe-Salpeter at finite temperature (digonalization solver) == | ||
In this section we will calculate the Bethe-Salpeter at finite temperature. You can generate the input using the command <code>yambo_ph -X s -o b -k sex -y d -V qp</code> | In this section we will calculate the Bethe-Salpeter at finite temperature. You can generate the input using the command <code>yambo_ph -X s -o b -k sex -y d -V qp</code> | ||
| Line 135: | Line 135: | ||
Notice that in the files you will find many exciton with negative energy due the full-BSE nature, finally consider line-width numbers with care due to the approximation described above. | Notice that in the files you will find many exciton with negative energy due the full-BSE nature, finally consider line-width numbers with care due to the approximation described above. | ||
== Bethe-Salpeter at finite temperature (inversion solver) == | |||
== Excitonic Eliashberg Functions == | == Excitonic Eliashberg Functions == | ||
Revision as of 12:06, 18 March 2021
In this tutorial we will show you how to calculate optical properties including thermal effects due to the electron-phonon coupling.
This tutorial assumes that you have completed all the steps from the previous tutorial on Electron Phonon Coupling.
The tutorial is dived in different steps first we will calculate absorption at independent particle approximation,
then we will include excitonic effects,
and finally we will show how to analyze the data.
Absorption at finite temperature
Now you repeat the previous calculation but including all k-points, the last 3 valence and the first 3 conduction bands:
..... %QPkrange # [GW] QP generalized Kpoint/Band indices 1|8|2|7| % ....
and save the results of the 0K and 300K temperature in two separate folder with the -J option. Now you can use the correction to the energy levels and the induced width to calculate the optical absorption at finite temperature. Generate the input with the command yambo_ph -o c -V qp
optics # [R] Linear Response optical properties
chi # [R][CHI] Dyson equation for Chi.
dipoles # [R] Oscillator strenghts (or dipoles)
Chimod= "IP" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% QpntsRXd
1 | 1 | # [Xd] Transferred momenta
%
% BndsRnXd
2 | 7 | # [Xd] Polarization function bands
%
% EnRngeXd
0.000000 | 5.000000 | eV # [Xd] Energy range
%
% DmRngeXd
0.0100000 | 0.0100000 | eV # [Xd] Damping range
%
ETStpsXd= 500 # [Xd] Total Energy steps
% LongDrXd
1.000000 | 0.000000 | 0.000000 | # [Xd] [cc] Electric Field
%
XfnQPdb= "E W < T300/ndb.QP" # [EXTQP Xd] Database action
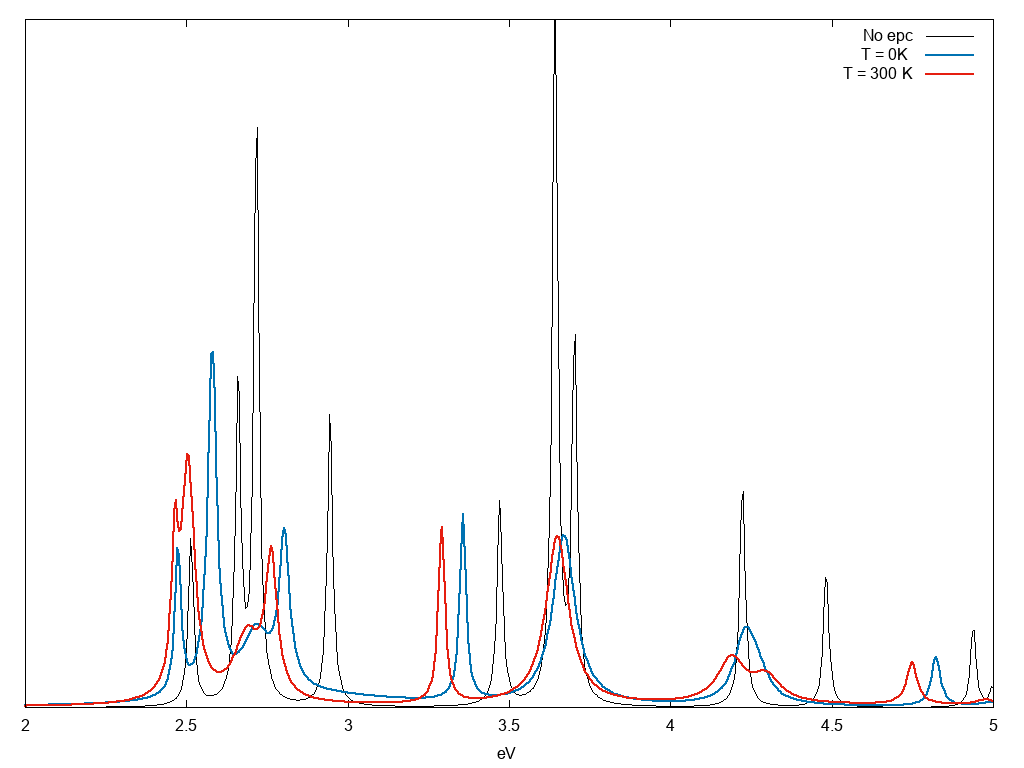
set the path of the ndb.QP you want to read and perform the calculations. Notice that from the QP database we read two quantities the correction to the energy levels E and the width W. In this calculation we also included a small smearing 0.01eV to mimic the electronic smearing. Hereafter the result without and with electron-phonon coupling at two different temperatures:
The temperature effect is clearly visible in the figure.
Bethe-Salpeter at finite temperature (digonalization solver)
In this section we will calculate the Bethe-Salpeter at finite temperature. You can generate the input using the command yambo_ph -X s -o b -k sex -y d -V qp
em1s # [R][Xs] Statically Screened Interaction optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. dipoles # [R] Oscillator strenghts (or dipoles) DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions Chimod= "HARTREE" # [X] IP/Hartree/ALDA/LRC/PF/BSfxc BSEmod= "coupling" # [BSE] resonant/retarded/coupling BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 9257 RL # [BSK] Exchange components BSENGBlk=-1 RL # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] #WehCpl # [BSK] eh interaction included also in coupling KfnQPdb= "E W < T0/ndb.QP" # [EXTQP BSK BSS] Database action KfnQP_INTERP_NN= 1 # [EXTQP BSK BSS] Interpolation neighbours (NN mode) KfnQP_INTERP_shells= 20.00000 # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode) KfnQP_DbGd_INTERP_mode= "NN" # [EXTQP BSK BSS] Interpolation DbGd mode % KfnQP_E 0.500000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % BSEprop= "abs" # [BSS] abs/kerr/magn/dichr trace % BSEQptR 1 | 1 | # [BSK] Transferred momenta range % % BSEBands 2 | 7 | # [BSK] Bands range % % BEnRange 0.00000 | 5.00000 | eV # [BSS] Energy range % % BDmRange 0.010000 | 0.010000 | eV # [BSS] Damping range % BEnSteps= 500 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field % #WRbsWF # [BSS] Write to disk excitonic the WFs XfnQPdb= "none" # [EXTQP Xd] Database action % BndsRnXs 1 | 12 | # [Xs] Polarization function bands % NGsBlkXs= 113 RL # [Xs] Response block size % LongDrXs 1.000000 | 0.000000 | 0.000000 | # [Xs] [cc] Electric Field % XTermKind= "none" # [X] X terminator ("none","BG" Bruneval-Gonze)
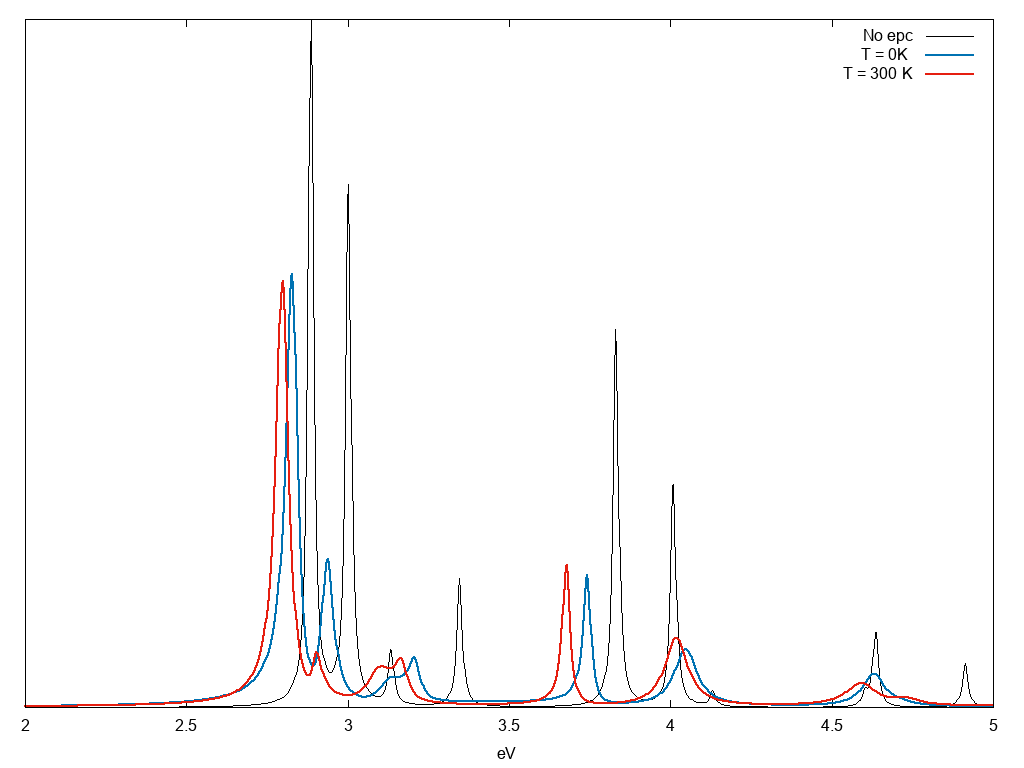
In this input file we asked Yambo to include finite temperature quasi-particle in the BSE with the line KfnQPdb= "E W < T0/ndb.QP" , notice that we also introduce an additional rigid shift of 0.8 eV to mimic the GW correction with the line 0.500000 | 1.000000 | 1.000000 | \# [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim. In principle you can calculate the GW correction following the this tutorial and then merge the corresponding ndb.QP database with the one of the electron-phonon coupling using the command ypp -qpdb m.
Notice that we changed the BSE type to "coupling" because you need the full Bethe-Salpeter to deal with complex quasi-particles.
Approximations:
In this calculation we have made different approximations:
1) we did not include the renormalization of excitons due to the change of the screening potential W with temperature. Including electron-phonon coupling
in the dielectric constant by changing the line XfnQPdb= "none" is unfortunately not enough, for a discussion see ref. [1]
2) The electron-phonon coupling should enter in the BSE through the exciton-phonon matrix elements and not from the single-particle self-energy, as we have done in this tutorial. The approximation used in this tutorial is valid for not too strong bound excitons, and in general it generated a finite life-time also for the lowest exciton in direct materials that is not correct. For a discussion see refs. [2][3] and [4].
3) we did not include scattering between exciton and phonons, therefore our results do not contain phonon-assisted absorption peaks, you can include these terms by finite difference displacements see refs. [3].
Result analysis
Results of BSE at finite temperature can be analized in the same way of standard BSE. You can plot exciton binging energy as a function of the temperature, exciton wave-function and so, see Exciton Plot tutorial.
For example if you sort exciton with the command ypp_ph -e s for the case T=0K, in addition to the exciton energy now you will find its line-width in the files .
o.exc_qpt1_E_sorted and o.exc_qpt1_I_sorted.
# # Maximum Residual Value = .72765E+05 # # E [ev] Strength Index W [meV] # ............... 3.13603616 0.894595146 274.000000 38.3100700 3.13607597 0.458951890 276.000000 38.3091507 3.13608289 0.936879739E-1 278.000000 38.3060684 3.13852167 0.135797265E-3 279.000000 36.6859016 3.13854289 0.166505214E-2 277.000000 36.6878891 3.13856506 0.185914442E-2 275.000000 36.6866493 3.18071890 0.344193308E-3 328.000000 35.5702744 3.18077826 0.227900382E-4 329.000000 35.5690689 3.19683385 0.355413969E-3 327.000000 34.4151421 3.23861122 0.210206732 330.000000 42.7790527 3.23862171 0.387398720 332.000000 42.7778893 3.23863339 0.522650003 331.000000 42.7766075
Notice that in the files you will find many exciton with negative energy due the full-BSE nature, finally consider line-width numbers with care due to the approximation described above.
Bethe-Salpeter at finite temperature (inversion solver)
Excitonic Eliashberg Functions
If you run the BSE and save the excitonic wave-functions (uncomment the flag WRbsWF in the BSE input file), tt is possible to plot the excitonic Eliashberg Functions with the command ypp_ph -e e.
For an interpretation of these functions see the discussion in reference [5]
Phonon-assisted density of states
Even if exciton-phonon scattering is not included in the BSE at finite temperature, it is possible to plot the phonon-assisted density of states (DOS) for light emission, defined as:
where Eql is the energy of the l-exciton at q-momentum, ωqλ is the phonon energy, nB is the Bose function, exciton are weighted with a Boltzamn factor and Emin is the lowest exciton energy in the all BZ.
In order to calculate these DOS you need to solve BSE for all the q-points for the lowest excitons, you can use SLEPC library to speed up calculations, then you need a converged phonon calculations.
Then you interpolate phonon on a dense phonon grid using matdyn.x utility in QE, and Yambo will interpolate exicton on the same grid.
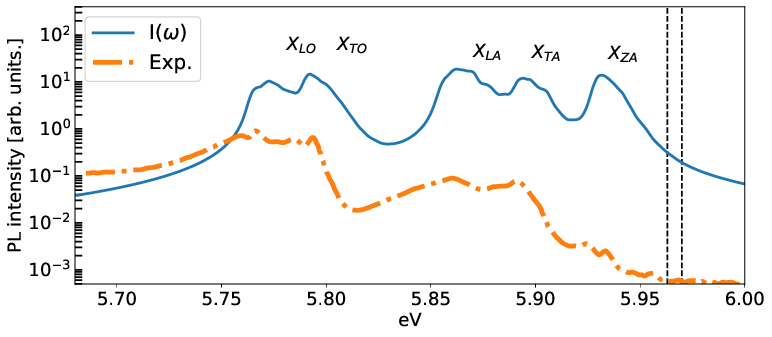
Here we present an example for hBN that is an indirect semiconductor.
Running ypp_ph -e p you will get:
BoseTemp= 50 K # Bosonic Temperature excitons # [R] Excitonic properties ph_ass_dos # [R] Phonon-assisted DOS States= "1 - 4" # Index of the BS state(s) PHfreqF= "./bn.freq_54" # PWscf format file containing the phonon frequencies % DOSERange 5.000000 | 5.500000 | eV # Energy range % DOSESteps= 1000 # Energy steps DOS_broad= 0.004 eV # Broadening of the DOS
where "bn.freq_54" is the file produced by matdyn.x with the input:
&input
asr='simple',
flfrc='bn.fc',
flfrq='bn.freq_54',
dos=.true.,
fldos='bn.dos',
ndos=2
nk1=54, nk2=54, nk3=18
/
and the BSE was calculated on a 18x18x6 grid. The final spectra will be:
where the DOS has been shifted to match the experimental peaks. Notice that the peak intensities are complitely off, because of the lack of the exciton-phonon matrix elements.
References
- ↑ L. Adamska and P. Umari, Phys. Rev. B 103, 075201 (2021)
- ↑ see Supp. Mat. of Phys. Rev. B 99, 081109(R) (2019)
- ↑ 3.0 3.1 F. Paleari, Phd Thesis (2019)
- ↑ H. Chen, D. Sangalli, and M. Bernardi Phys. Rev. Lett. 125, 107401 (2020)
- ↑ Andrea Marini Phys. Rev. Lett. 101, 106405 (2008)