Optical properties at finite temperature

Yambo tutorial image

In this tutorial we will show you how to calculate optical properties including thermal effects due to the electron-phonon coupling.
This tutorial assumes that you have completed all the steps from the previous tutorial on Electron Phonon Coupling.
The tutorial is dived in different steps first we will calculate absorption at independent particle approximation,
then we will include excitonic effects, and finally we will show how to analyze the data.

Absorption at finite temperature

Now you repeat the previous calculation but including all k-points, the last 3 valence and the first 3 conduction bands:

.....
%QPkrange                        # [GW] QP generalized Kpoint/Band indices
1|8|2|7|
%
....

and save the results of the 0K and 300K temperature in two separate folder with the -J option. Now you can use the correction to the energy levels and the induced width to calculate the optical absorption at finite temperature. Generate the input with the command yambo_ph -o c -V qp

optics                           # [R] Linear Response optical properties
chi                              # [R][CHI] Dyson equation for Chi.
dipoles                          # [R] Oscillator strenghts (or dipoles)
Chimod= "IP"                     # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% QpntsRXd
 1 | 1 |                             # [Xd] Transferred momenta
%
% BndsRnXd
  2 |  7 |                           # [Xd] Polarization function bands
%
% EnRngeXd
 0.000000 | 5.000000 |         eV    # [Xd] Energy range
%
% DmRngeXd
 0.0100000 | 0.0100000 |         eV    # [Xd] Damping range
%
ETStpsXd=  500                   # [Xd] Total Energy steps
% LongDrXd
 1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
%
XfnQPdb= "E W < T300/ndb.QP"      # [EXTQP Xd] Database action

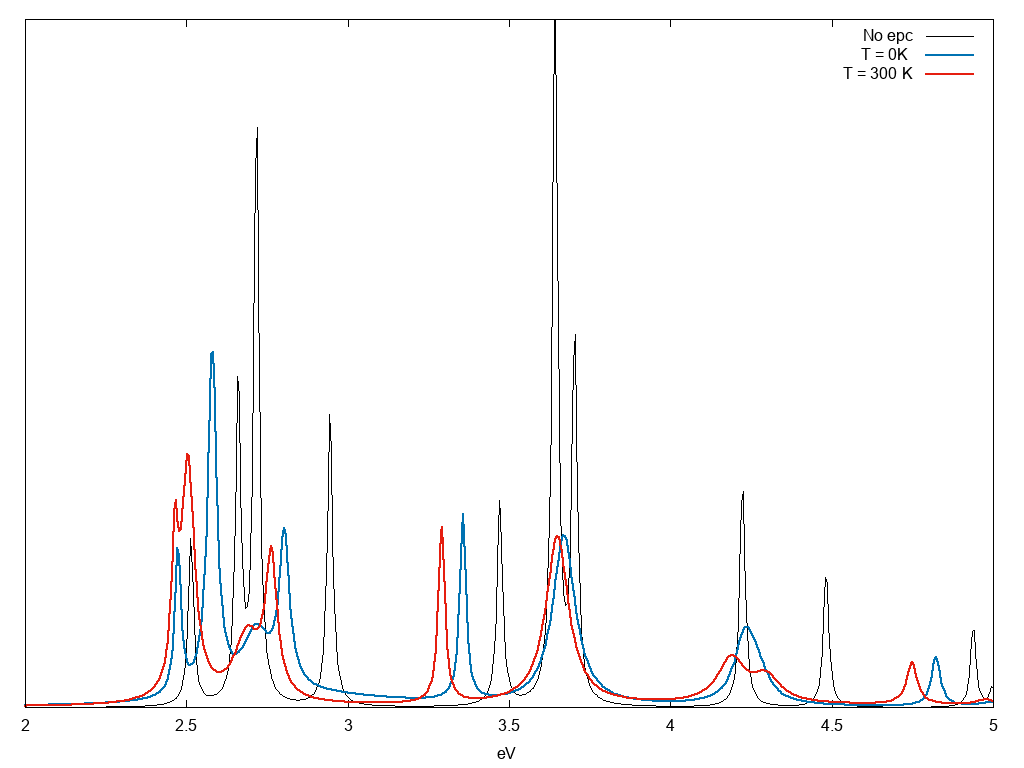
set the path of the ndb.QP you want to read and perform the calculations. Notice that from the QP database we read two quantities the correction to the energy levels E and the width W. In this calculation we also included a small smearing 0.01eV to mimic the electronic smearing. Hereafter the result without and with electron-phonon coupling at two different temperatures:

The temperature effect is clearly visible in the figure.

Bethe-Salpeter at finite temperature

In this section we will calculate the Bethe-Salpeter at finite temperature. You can generate the input using the command yambo_ph -X s -o b -k sex -y d -V qp

em1s                             # [R][Xs] Statically Screened Interaction
optics                           # [R] Linear Response optical properties
bss                              # [R] BSE solver
bse                              # [R][BSE] Bethe Salpeter Equation.
dipoles                          # [R] Oscillator strenghts (or dipoles)
DIP_Threads=0                    # [OPENMP/X] Number of threads for dipoles
X_Threads=0                      # [OPENMP/X] Number of threads for response functions
K_Threads=0                      # [OPENMP/BSK] Number of threads for response functions
Chimod= "HARTREE"                # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
BSEmod= "resonant"               # [BSE] resonant/retarded/coupling
BSKmod= "SEX"                    # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
BSSmod= "d"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
BSENGexx=  9257            RL    # [BSK] Exchange components
BSENGBlk=-1                RL    # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)]
#WehCpl                        # [BSK] eh interaction included also in coupling
KfnQPdb= "E W < T0/ndb.QP"       # [EXTQP BSK BSS] Database action
KfnQP_INTERP_NN= 1               # [EXTQP BSK BSS] Interpolation neighbours (NN mode)
KfnQP_INTERP_shells= 20.00000    # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode)
KfnQP_DbGd_INTERP_mode= "NN"     # [EXTQP BSK BSS] Interpolation DbGd mode
% KfnQP_E
  0.800000 | 1.000000 | 1.000000 |        # [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim
%
BSEprop= "abs"                   # [BSS] abs/kerr/magn/dichr trace
% BSEQptR
 1 | 1 |                             # [BSK] Transferred momenta range
%
% BSEBands
   2 |  7 |                           # [BSK] Bands range
%
% BEnRange
  0.00000 | 5.00000 |         eV    # [BSS] Energy range 
%
% BDmRange
  0.010000 | 0.010000 |         eV    # [BSS] Damping range
%
BEnSteps= 500                    # [BSS] Energy steps
% BLongDir 
 1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
%
#WRbsWF                        # [BSS] Write to disk excitonic the WFs
XfnQPdb= "none"                  # [EXTQP Xd] Database action
% BndsRnXs
  1 | 12 |                           # [Xs] Polarization function bands
%
NGsBlkXs= 113              RL    # [Xs] Response block size
% LongDrXs
 1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
%
XTermKind= "none"                # [X] X terminator ("none","BG" Bruneval-Gonze)

In this input file we asked Yambo to include finite temperature quasi-particle in the BSE with the line KfnQPdb= "E W < T0/ndb.QP" , notice that we also introduce an additional rigid shift of 0.8 eV to mimic the GW correction with the line 0.800000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim. In principle you can calculate the GW correction following the this tutorial and then merge the corresponding ndb.QP database with the one of the electron-phonon coupling using the command ypp -qpdb m. The same procedure can be applied to the Bethe-Salpeter calculations. However in this case results can be slightly wrong. If fact electron-phonon matrix elements should be rotate in the excitonic space, as it was done in ref. , while at present Yambo calculate the exciton width from the correction to the single particle bands, see ref. . This approximation is correct in case of not-strong bounded excitons, and unfortunately this is not the case.