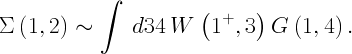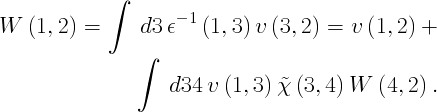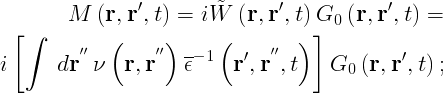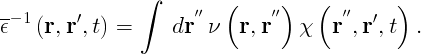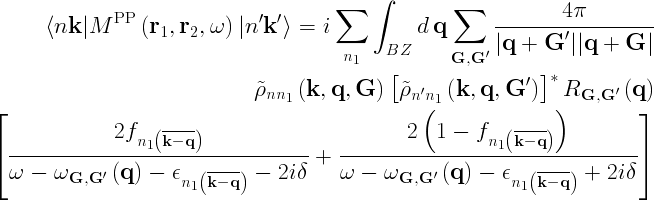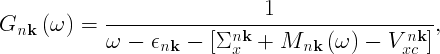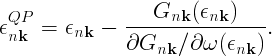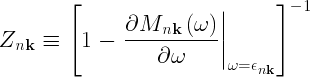The GW approximation

The GW approximation

The gowo runlevel solves the Dyson equation ( G ) using the GW approximation for the self-energy operator. This approximation is currently one of the most successful approximation for self-energy operator and has yielded remarkably accurate band structures for many materials. The GW approximation is obtained as first term in the expansion of Hedin equations in the expansion in the screened interaction W

The screening interaction is defined as

The first term on the r.h.s. gives the exchange self-energy ([[../docs/doc_XX.php|XX]]), while the second term gives the frequency dependent part of the screening interaction. Starting from the non-interacting Green's function described in [[../docs/doc_G.php|G]] a first approximation to the (irreducible) response function is constructed

This is used to construct the screened interaction W, and finally, the self-energy operator. At this point the Dyson equation should be solved self-consistently (to be conserving). As this scheme would be computationally too demanding, practical schemes neglects or approximates the self-consistency. Moreover approximations are introduced to make feasible the calculation of the screened interaction W.

The plasmon-pole approximation

This runlevel calculates only the frequency dependent part of the self-energy operator, the mass operator

with the frequency dependent screening function defined as

Using the plasmon pole approximation for the screening function ([[../docs/doc_Xp.php|Xp]]) it is possible to obtain an analytical expression for the matrix elements of the mass operator:

The maximum vectors in the reciprocal lattice summation is determined by [[../vars/../vars/var_NGsBlk.php|NGsBlk]] , while the range of the bands summation is given by [[../vars/../vars/var_GbndRnge.php|GbndRnge]] . [[../vars/../vars/var_QPkrange.php|QPkrange]] (or alternatively [[../vars/../vars/var_QPerange.php|QPErange]] ) selects the matrix elements to calculate.

Dyson equation: solvers for the QP energies

The Dyson equation

with

can be solved by using either Newton or the secant root-finding algorithm ( [[../vars/../vars/var_DysSolver.php|DysSolver]] set to 'n' or 's'). The Newton method uses the first order of the Taylor series of a function in the vicinity of a root to evaluate the correction to the initial guess:

This leads to

with Z (the renormalization factor) defined

The derivative of the self-energy with respect to the frequency is calculated from finite differences. The flag [[../vars/../vars/var_NewtDchk.php|NewtDchk]] enables the test on the convergence of this quantity. The secant method: nothing yet

References

• F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys. 61, 237-312 (1998)
• G. Baym abd L. P. Kadanoff, Phys. Rev. 124, 287 (1961)
• Arno Schindlmayr, P. Garcia-Gonzalez, and R. W. Godby Phys. Rev. B 64, 235106 (2001)