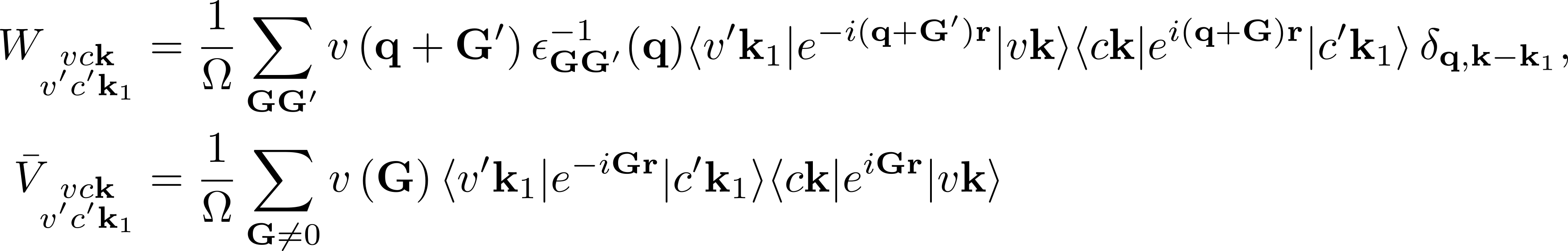Bethe-Salpeter kernel: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
In this module you will learn how to calculate the matrix elements of the Bethe-Salpeter kernels. This is a fundamental step in the calculation of optical spectra within the Bethe-Salpeter equation framework. | |||
==Background== | |||
To solve the Bethe-Salpeter equations the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. The two-particle Hamiltonian matrix elements are given by: | |||
[[File:BSE1-Eq1.png|none|x50px]] | |||
where ''vc'''''k''' indicates the pair of quasiparticle states ''v'''''k''' and ''c'''''k'''. | |||
The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part ''V'' (which stems from the Hartree potential) and the electron-hole attraction part ''W'' (which stems from the screened exchange potential). The kernel both shifts (diagonal contributions) and couples (off-diagonal contributions) the quasiparticle energy differences: | |||
[[File:BSE1_Eq3.png|none|x100px]] | [[File:BSE1_Eq3.png|none|x100px]] | ||
==Prerequisites== | |||
==Choosing input parameters== | |||
Start by generating the input by invoking yambo with the option "-o b -k bse -V qp" from the command line: | Start by generating the input by invoking yambo with the option "-o b -k bse -V qp" from the command line: | ||
| Line 36: | Line 42: | ||
Alternatively we can directly input corrections calculated from a previous GW calculation as we will learn later in this tutorial. | Alternatively we can directly input corrections calculated from a previous GW calculation as we will learn later in this tutorial. | ||
==Bethe-Salpeter kernel runlevel== | |||
Run the calculation by invoking yambo in the command line: | Run the calculation by invoking yambo in the command line: | ||
$ yambo -F 02_3D_BSE_kernel.in -J 3D_BSE | $ yambo -F 02_3D_BSE_kernel.in -J 3D_BSE | ||
| Line 56: | Line 63: | ||
3D_BSE/ndb.BS_Q1 | 3D_BSE/ndb.BS_Q1 | ||
==Summary== | |||
==Links== | |||
<-- | <!--''Prerequisites'' | ||
Run [[Initialization]] | Run [[Initialization]] | ||
Revision as of 18:51, 16 April 2017
In this module you will learn how to calculate the matrix elements of the Bethe-Salpeter kernels. This is a fundamental step in the calculation of optical spectra within the Bethe-Salpeter equation framework.
Background
To solve the Bethe-Salpeter equations the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. The two-particle Hamiltonian matrix elements are given by:
where vck indicates the pair of quasiparticle states vk and ck. The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part V (which stems from the Hartree potential) and the electron-hole attraction part W (which stems from the screened exchange potential). The kernel both shifts (diagonal contributions) and couples (off-diagonal contributions) the quasiparticle energy differences:
Prerequisites
Choosing input parameters
Start by generating the input by invoking yambo with the option "-o b -k bse -V qp" from the command line:
$ yambo -o b -k bse -V qp -F 02_3D_BSE_kernel.in
The input opens in the standard editor. The relevant input parameters to be changed are
BSENGexx = 30 Ry BSENGBlk = 4 Ry % BSEBands 6 | 10 | %
The first two are the cutoff for the summations on the reciprocal lattice vectors which appear in the expressions for V (BSENGexx) and W (BSENGBlk) here above.
The third parameter gives the range of quasiparticle states (their band index) that define the basis of quasiparticle pairs that we need to describe the excitons (in the energy range of interest). For example since we have 8 occupied bands, here we consider the pairs of bands: 6-9, 6-10, 7-9, 7-10, 8-9, 8-10 (those are 6 pairs of bands = 2 valence times 3 conduction bands).
For each of those pairs we then consider all k points in the Brillouin zone available from the DFT calculations. Since we have a 6 x 6 x 2 grid, this amounts to 72 k points in the Brillouin zone.
Then finally we are using a basis of 6 x 72 = 432 vck pairs to represent the excitons of the system.
The values for these 3 parameters are chosen from convergence studies, as discussed in the next tutorial.
Another parameter to modify is
% KfnQP_E 1.440000 | 1.000000 | 1.000000 | %
This gives the quasiparticle corrections to the Kohn-Sham eigenvalues and is deduced either from experiment or previous GW calculations. The corrections consist in a shift (first value) of the conduction bands in eV and renormalization of the conduction and valence bandwidths (second and third value). Alternatively we can directly input corrections calculated from a previous GW calculation as we will learn later in this tutorial.
Bethe-Salpeter kernel runlevel
Run the calculation by invoking yambo in the command line:
$ yambo -F 02_3D_BSE_kernel.in -J 3D_BSE
In the log (either in standard output or in l_optics_bse_bsk), after various setup/loading, the kernel is calculated:
<01s> [05.04.03] Kernel loop <02s> Kernel |########################################| [100%] --(E) --(X)
In the report r_optics_bse_bsk the information relative to this runlevel are reported under the section:
[05] Response Functions in Transition space ===========================================
Take some time to inspect the log and the report. For example try to find where the input parameters are reported, the dimension of the 2-particle hamiltonian and if these match your expectations.
This run does not produce any human readable output. The kernel is stored in a database in the 3D_BSE directory
3D_BSE/ndb.BS_Q1