Exciton-phonon coupling and luminescence: Difference between revisions
| (58 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
In this advanced tutorial, we will calculate exciton-phonon interactions from first principles by interfacing DFPT (for phonon calculations) and BSE (for exciton calculations). | In this advanced tutorial, we will calculate exciton-phonon interactions from first principles by interfacing DFPT (for phonon calculations) and BSE (for exciton calculations). | ||
The DFTP calculations are run with Quantum ESPRESSO, while the many-body GW-BSE calculations are run with Yambo. Finally, the exciton-phonon interaction will be obtained by combining and postprocessing the databases computed in the two previous runs. The great advantage of this workflow is that the calculations can be run in the irreducible Brillouin zones both for the electronic momenta ( | The DFTP calculations are run with Quantum ESPRESSO, while the many-body GW-BSE calculations are run with Yambo. Finally, the exciton-phonon interaction will be obtained by combining and postprocessing the databases computed in the two previous runs. The great advantage of this workflow is that the calculations can be run in the irreducible Brillouin zones both for the electronic momenta ('''k''') and the transfer momenta ('''Q''', '''q''') of excitons and phonons, thus speeding up considerably the jobs while reducing the IO and memory load. | ||
We will first compute the exciton-phonon coupling matrix elements: these are the building blocks needed to construct experimental observables such as phonon-assisted optical spectra (such as luminescence), Raman spectra and exciton lifetimes. We will do this in the case of monolayer | We will first compute the exciton-phonon coupling matrix elements: these are the building blocks needed to construct experimental observables such as phonon-assisted optical spectra (such as luminescence), Raman spectra and exciton lifetimes. We will do this in the case of monolayer MoS<sub>2</sub>, a 2D system with large spin-orbit interaction. | ||
As an example of application, we will consider the case of phonon-assisted luminescence. We will do this in the case of bulk hBN, a layered indirect insulator with strong electron-phonon coupling. | As an example of application, we will consider the case of phonon-assisted luminescence. We will do this in the case of bulk hBN, a layered indirect insulator with strong electron-phonon coupling. | ||
| Line 17: | Line 17: | ||
Also, we assume that you already know how to run both a basic '''Yambo''' GW-BSE calculation and a DFPT phonon calculation with '''Quantum ESPRESSO'''. | Also, we assume that you already know how to run both a basic '''Yambo''' GW-BSE calculation and a DFPT phonon calculation with '''Quantum ESPRESSO'''. | ||
Besides the QE executables <code>pw.x</code> and <code>ph.x</code>, we also use the yambo phonon-specific executable <code>yambo_ph</code> and the python utility '''Yambopy'''. The auxiliary code '''LetzElPhC''' (executable <code>lelphc</code>) will be used to obtain the electron-phonon matrix elements by reading the same electronic wavefunctions used by Yambo (and stored in the <code>SAVE</code> directory), while also making full use of crystal symmetries. [https://gitlab.com/lumen-code/LetzElPhC LetzElPhC] will be run by Yambopy, but it must nonetheless be installed. Finally, the exciton-phonon properties can be computed either using <code>yambo_ph</code> or using Yambopy itself. | Besides the QE executables <code>pw.x</code> and <code>ph.x</code>, we also use the yambo phonon-specific executable <code>yambo_ph</code> and the python utility '''Yambopy'''. The auxiliary code '''LetzElPhC''' (executable <code>lelphc</code>) will be used to obtain the electron-phonon matrix elements by reading the same electronic wavefunctions used by Yambo (and stored in the <code>SAVE</code> directory), while also making full use of crystal symmetries. [https://gitlab.com/lumen-code/LetzElPhC LetzElPhC] will be run by Yambopy, but it must nonetheless be installed. Finally, the exciton-phonon properties can be computed either using <code>yambo_ph</code> or using Yambopy itself. Both cases will be covered in this tutorial. | ||
[[File:Workflow scheme.png|800px|center]] | [[File:Workflow scheme.png|800px|center]] | ||
| Line 196: | Line 196: | ||
X_and_IO_nCPU_LinAlg_INV=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) | X_and_IO_nCPU_LinAlg_INV=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) | ||
Chimod= "hartree" # [X] IP/Hartree/ALDA/LRC/BSfxc | Chimod= "hartree" # [X] IP/Hartree/ALDA/LRC/BSfxc | ||
% BndsRnXs | % BndsRnXs | ||
1 | 200 | # [Xs] Polarization function bands | 1 | 200 | # [Xs] Polarization function bands | ||
| Line 205: | Line 202: | ||
1.000000 | 1.000000 | 1.000000 | # [Xs] [cc] Electric Field | 1.000000 | 1.000000 | 1.000000 | # [Xs] [cc] Electric Field | ||
% | % | ||
NGsBlkXs= | NGsBlkXs= 8000 mRy # [Xs] Response block size | ||
<span style="color:blue"># BSE</span> | <span style="color:blue"># BSE</span> | ||
BS_CPU= "4.1.2" # [PARALLEL] CPUs for each role | BS_CPU= "4.1.2" # [PARALLEL] CPUs for each role | ||
| Line 212: | Line 209: | ||
BSEmod= "causal" # [BSE] resonant/causal/coupling | BSEmod= "causal" # [BSE] resonant/causal/coupling | ||
BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc | BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc | ||
BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(i)nversion/(t)ddft` | BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` | ||
BSENGexx= | BSENGexx= 40000 mRy # [BSK] Exchange components | ||
ALLGexx # [BSS] Force the use use all RL vectors for the exchange part | ALLGexx # [BSS] Force the use use all RL vectors for the exchange part | ||
BSENGBlk= | BSENGBlk= 8000 mRy # [BSK] Screened interaction block size | ||
<span style="color:red">Lkind="full" #[BSE,X] bar(default)/full/tilde</span> | <span style="color:red">Lkind="full" #[BSE,X] bar(default)/full/tilde</span> | ||
% KfnQP_E | % KfnQP_E | ||
| Line 238: | Line 235: | ||
WRbsWF # [BSS] Write to disk excitonic the FWs | WRbsWF # [BSS] Write to disk excitonic the FWs | ||
This file was generated using the command: <code> yambo -X s -o b -k sex -y d -r</code><br> | |||
First of all, we compute the excitons for all the momenta in the irreducible Brillouin zone for our discrete grid via the <code>BSEQptR</code> variable. This will be a '''finite-momentum''' BSE calculation, analogous to the phonon one. | First of all, we compute the excitons for all the momenta in the irreducible Brillouin zone for our discrete grid via the <code>BSEQptR</code> variable. This will be a '''finite-momentum''' BSE calculation, analogous to the phonon one. | ||
| Line 260: | Line 259: | ||
yambopy l2y | yambopy l2y | ||
to see the help for the calculation. For example, if we want to do a serial run of LetzElPhC for bands from <math>n_i</math> to <math>n_f</math>, we should type: | to see the help for the calculation. Have a look at the various flags and their description. | ||
For example, if we want to do a serial run of LetzElPhC for bands from <math>n_i</math> to <math>n_f</math>, we should type: | |||
yambopy l2y -ph path/of/ph_input.in -b n_i n_f | yambopy l2y -ph path/of/ph_input.in -b n_i n_f | ||
Here <math>n_i</math> and <math>n_f</math> are integers representing the initial and final band indices. | Here <math>n_i</math> and <math>n_f</math> are integers representing the initial and final band indices. '''Please note''': in this case, the band index starts from 1 and the the interval of bands read by the code is <math>[n_i,n_f]</math> including the extrema of the interval. | ||
These should coincide with those used for the Bethe-Salpeter kernel, i.e. those specified in the <code>BSEBands</code> variable of the BSE input file (this is not strictly necessary, but certainly efficient since these calculations use a lot of disk space). | These should coincide with those used for the Bethe-Salpeter kernel, i.e. those specified in the <code>BSEBands</code> variable of the BSE input file (this is not strictly necessary, but certainly efficient since these calculations use a lot of disk space). | ||
| Line 270: | Line 270: | ||
For our system, we want to do a parallel calculation with 4 qpools and 2 kpools. In addition, we want to explicitly specify the path of the <code>lelphc</code> executable and avoid automatically deleting the LetzElPhC data. So we type: | For our system, we want to do a parallel calculation with 4 qpools and 2 kpools. In addition, we want to explicitly specify the path of the <code>lelphc</code> executable and avoid automatically deleting the LetzElPhC data. So we type: | ||
yambopy l2y -ph path/of/dvscf/mos2.dvscf -b 25 28 -par 4 2 -lelphc path/to/lelphc_exe | yambopy l2y -ph path/of/dvscf/mos2.dvscf -b 25 28 -par 4 2 -lelphc path/to/lelphc_exe | ||
At the end, check your directory: you should find the <code>lelphc.in</code> input file that was run, let's inspect it: | |||
# LetzElPhC input for yambo generated by yambopy | # LetzElPhC input for yambo generated by yambopy | ||
| Line 290: | Line 284: | ||
convention = yambo | convention = yambo | ||
Notice the variable <code>convention=yambo</code>: what does it mean? At variance with QE and many other codes, Yambo uses the "backward" momentum transfer convention for electronic scatterings. That is, an electronic transition goes from band <math>n</math> and momentum <math>k-q</math> to band <math>m</math> and momentum <math>k</math>. In the "forward" momentum transfer convention (the more standard one), the transitions go from <math>nk</math> to <math>mk+q</math>. Therefore, this variable ensures that the electron-phonon coupling matrix elements are computed as <math>\langle mk|dV|nk-q\rangle</math>. This will have consequences also in the formulation of the ''exciton''-phonon coupling matrix element. | |||
You will also find a <code>ndb.elph</code> database that contains the computed electron-phonon matrix elements, in the output format of <code>LetzElPhC</code>. | |||
In addition, if you check the <code>SAVE</code> folder: | |||
ls SAVE/ndb.elph_gkkp* | |||
you will see that yambopy has created the Yambo-compatible electron-phonon databases. | |||
If you want to run LetzElPhC directly, without using yambopy, you can refer to its [[https://gitlab.com/lumen-code/LetzElPhC/-/blob/main/docs/main.pdf?ref_type=heads|user guide]]. | |||
Keep in mind that in this case, in order to convert the database to the <code>ndb.elph_gkkp*</code> databases of Yambo, you will then need a couple of lines of python using the Yambopy class <code>ConvertElectronPhononDB</code> in <code>yambopy/letzelph_interface/lelph2y.py</code>. | |||
If you don't need the <code>ndb.elph_gkkp*</code> databases -- e.g., because you are doing the exc-ph postprocessing with yambopy -- you can run <code>yambopy l2y ...</code> with the <code>--no_gkkp</code> option. | |||
If you don't need the <code>ndb.elph</code> databases -- e.g., because you are using <code>yambo_ph</code> for the exc-ph part -- you can run <code>yambopy l2y ...</code> with the <code>--no_lelphc_dbs</code> option. | |||
== Step 7: Obtain the exciton-phonon coupling == | == Step 7: Obtain the exciton-phonon coupling == | ||
Now, we can finally access our basic building block for exciton-phonon physics. This could be done entirely in python (using '''Yambopy'''), or by running '''Yambo'''. | Now, we can finally access our basic building block for exciton-phonon physics. This could be done entirely in python (using '''Yambopy'''), or by running '''Yambo'''. | ||
* For the <span style="color:red">'''Yambo postprocessing'''</span> case (running yambo inputs with the <code>yambo_ph</code> executable), <span style="color:red">'''follow the alternative route to Steps 7-8 [[Exciton-phonon coupling and luminescence - Yambo postprocessing|at this link]]'''</span>. | |||
* For the <span style="color:red">'''Yambopy postprocessing'''</span> case (using flexible python scripting), <span style="color:red">'''keep following Steps 7-8 on this page'''</span>. | |||
Our objective is obtaining the following quantity: | Our objective is obtaining the following quantity: | ||
<math>\mathcal{G}^\mu_{\alpha\lambda}(0,q)=\sum_{vv^\prime c k} A^{\alpha, *}_{cv^\prime} (k, q) g_{vv^\prime}^\mu (k,q) A^{\lambda}_{cv}(k, | <math>\mathcal{G}^\mu_{\alpha\lambda}(0,q)=\sum_{vv^\prime c k} A^{\alpha, *}_{cv^\prime} (k, q) g_{vv^\prime}^\mu (k,q) A^{\lambda}_{cv}(k,0) - \sum_{cc^\prime vk} A^{\alpha, *}_{c^\prime v} (k+q, q) g_{c^\prime c}^\mu (k+q,q) A^{\lambda}_{cv}(k, 0)</math> | ||
Here, <math>A^{\ | Here, <math>A^{\alpha}_{cv}(k,q)</math> are the exciton coefficients extracted from the eigenvector of the two-particles Hamiltonian during the BSE calculation in step 5, while <math>g_{nm}^\mu (k,q)</math> are the electron-phonon coupling matrix elements obtained in step 6. As you can see, the exciton <math>\lambda</math> undergoes phonon-mediated scattering to state <math>\alpha</math> via phonon mode <math>\mu</math>. The scattering can happen for the hole (valence, <math>v</math>) or for the electron (conduction, <math>c</math>). | ||
NB: | NB: | ||
| Line 310: | Line 320: | ||
(2) For simplicity, this is written for zero initial exciton momentum. This means that one of the two states involved in the phonon-mediated scattering process will be in the optical limit (and possibly an optically generated exciton), while the other state can have any momentum: this momentum will be the same as the phonon one. This matrix element can be used to describe phonon-assisted absorption and emission spectra. | (2) For simplicity, this is written for zero initial exciton momentum. This means that one of the two states involved in the phonon-mediated scattering process will be in the optical limit (and possibly an optically generated exciton), while the other state can have any momentum: this momentum will be the same as the phonon one. This matrix element can be used to describe phonon-assisted absorption and emission spectra. | ||
In order to calculate this quantity using python, we need the <code>ndb.elph</code> databases natively generated by the <code>LetzElPhC</code> code, as well as the BSE databases <code>ndb.BS_diago_Q*</code> containing the information on exciton wavefunctions and energies. | |||
Next, we write a python user script importing the yambopy exciton-phonon tools. You can find a version of this script in <code>yambopy/tutorials/exciton-phonon/calculate_excph.py</code>. | |||
import numpy as np | |||
from yambopy import YamboLatticeDB,YamboWFDB,LetzElphElectronPhononDB <span style="color:blue">#Specific Yambopy dbs loading classes</span> | |||
from yambopy.exciton_phonon.excph_matrix_elements import exciton_phonon_matelem <span style="color:blue">#Specific exc-ph functions</span> | |||
path = '1L_MoS2' | |||
bands_range=[24,28] <span style="color:blue"># 2 valence bands, 2 conduction bands</span> | |||
nexc = 12 <span style="color:blue"># number of excitonic states</span> | |||
bsepath = f'{path}/bse-allq_full' <span style="color:blue"># Path to BSE calculation (Lin=Lout)</span> | |||
savepath = f'{path}/SAVE' <span style="color:blue"># Yambo SAVE</span> | |||
ndb_elph = f'{path}/ndb.elph' <span style="color:blue"># LetzElPhC electron-phonon database (any convention)</span> | |||
<span style="color:blue"># Read lattice</span> | |||
lattice = YamboLatticeDB.from_db_file(filename=f'{savepath}/ns.db1') | |||
<span style="color:blue"># Read electron-phonon</span> | |||
elph = LetzElphElectronPhononDB(ndb_elph,read_all=False) | |||
<span style="color:blue"># Read wave functions</span> | |||
wfcs = YamboWFDB(filename='ns.wf',save=savepath,latdb=lattice,bands_range=bands_range) | |||
<span style="color:blue"># Calculate exciton-phonon matrix elements</span> | |||
exph = exciton_phonon_matelem(lattice,elph,wfcs,BSE_dir=bsepath,neigs=nexc,dmat_mode='save',exph_file='MoS2_Ex-ph.npy') | |||
In this | In this script, we can select the number exciton states <math>\lambda</math> with <code>nexc</code>, the single-particle bands range with <code>bands_range</code>. '''Please note''': in this case, the band index starts from 0 (python indexing) and the the interval of bands read by the code is <math>[n_i,n_f)</math>, therefore the last value (28 in the example) is excluded. That is, in the example we are selecting the 25th, 26th, 27th and 28th bands. Those bands have to be present in both the electron-phonon and BSE calculations. | ||
Here we calculate the couplings of the first twelve states at each finite-<math>q</math> point including <math>q=0</math>. We also include all the nine phonon modes of monolayer MoS2. We also need access to the Yambo <code>SAVE</code> directory in order to read the electronic wavefunctions: they are used to compute the electronic representation matrices (<code>dmat</code> in the code). The argument <code>dmat_mode</code> can be set to <code>'load'</code> for subsequent calculations. | |||
When we are satisfied with the input, we run the code | When we are satisfied with the input, we run the code: | ||
python calculate_excph.py | |||
If you check the output, you should find the <code> | If you check the output, you should find the <code>MoS2_Ex-ph.npy</code> binary file in the directory where you ran. | ||
=== Analysis of the couplings === | === Analysis of the couplings === | ||
| Line 348: | Line 363: | ||
It is also not easy to meaningfully plot this quantity. We have to make sure that we are not breaking degenerate states, otherwise the plots will not be invariant. | It is also not easy to meaningfully plot this quantity. We have to make sure that we are not breaking degenerate states, otherwise the plots will not be invariant. | ||
First of all, we have to know our system: in monolayer | First of all, we have to know our system: in monolayer MoS<sub>2</sub>, the first four excitons are all doubly degenerate. The first exciton responsible for a bright peak in the absorption spectrum (the '''A''' peak), is the second state, corresponding to state indices <code>(3,4)</code> in fortran indexing or <code>(2,3)</code> in python indexing. | ||
All these information can be obtained by analyzing the BSE results (this stuff is explained in the BSE tutorials) and by knowledge of the system or class of systems from the literature. | All these information can be obtained by analyzing the BSE results (this stuff is explained in the BSE tutorials) and by knowledge of the system or class of systems from the literature. | ||
| Line 356: | Line 371: | ||
<math>F_A(q)= \sqrt{ \sum_{\alpha \in A,\lambda,\mu} |\mathcal{G}_{\alpha\lambda}^\mu (0,q)|^2 }</math> | <math>F_A(q)= \sqrt{ \sum_{\alpha \in A,\lambda,\mu} |\mathcal{G}_{\alpha\lambda}^\mu (0,q)|^2 }</math> | ||
In order to do this, we create a python script <code>analyse_excph.py</code> in which we first load the excph dabatases | In order to do this, we create a python script <code>analyse_excph.py</code> in which we first load the excph dabatases. | ||
You can find this script in the yambopy directory, in <code>tutorials/exciton-phonon</code>. | You can find a version of this script in the yambopy directory, in <code>tutorials/exciton-phonon</code>. | ||
First, we select the exciton and phonon states to be included in <code>F_A</code>, together with the path of databases and plot details: | First, we select the exciton and phonon states to be included in <code>F_A</code>, together with the path of databases and plot details: | ||
# Exciton in states | <span style="color:blue"># Exciton "in" states</span> | ||
exc_in = [2,3] | exc_in = [2,3] <span style="color:blue"># First bright peak (A: 2,3 -- B: 6,7)</span> | ||
exc_out = [0,1,2,3] # first 4 states (dispersion of triplet state and A) | exc_out = [0,1,2,3] <span style="color:blue"># first 4 states (dispersion of dark triplet state and A)</span> | ||
ph_in = 'all' | ph_in = 'all' | ||
<span style="color:blue"># Paths of databases</span> | |||
ns_db1 =f'{path}/SAVE/ns.db1' | ns_db1 =f'{path}/SAVE/ns.db1' | ||
ns_ypy = 'MoS2_Ex-ph.npy' | |||
... | ... | ||
| Line 373: | Line 387: | ||
Then, we load the data: | Then, we load the data: | ||
# Read lattice and k-space info | <span style="color:blue"># Read lattice and k-space info</span> | ||
ylat = YamboLatticeDB.from_db_file(filename=ns_db1 | ylat = YamboLatticeDB.from_db_file(filename=ns_db1) | ||
print(ylat) | print(ylat) | ||
# | <span style="color:blue"># Load exc-ph database</span> | ||
X_py = np.load(ns_ypy) | |||
G_squared = np.abs(X_py)**2. | |||
The quantity <math>F_A(q)</math> is | The quantity <math>F_A(q)</math> is obtained from a dedicated function as: | ||
if exc_in == 'all': exc_in = range(G_squared.shape[2]) | if exc_in == 'all': exc_in = range(G_squared.shape[2]) | ||
| Line 394: | Line 405: | ||
G_squared = G_squared[:, exc_out].sum(axis=(1)) | G_squared = G_squared[:, exc_out].sum(axis=(1)) | ||
F_q = np.sqrt( G_squared )*ha2ev # Switch from Ha to eV | F_q = np.sqrt( G_squared )*ha2ev <span style="color:blue"># Switch from Ha to eV</span> | ||
And finally, we have to make a plotting function. For this tutorial we will use the | And finally, we have to make a plotting function. For this tutorial we will use a custom scatterplot employing some of the plotting tools provided by yambopy (but you can do whatever you want). | ||
plot_2D_excph(qgrid,G2_to_plot,rlat=ylat.rlat,plt_cbar=True,\ | |||
marker='H',s=700,cmap='magma') | |||
... | ... | ||
You can get more experience on using Yambopy for these kinds of visualization by following the [https://wiki.yambo-code.eu/wiki/index.php?title=First_steps_in_Yambopy Yambopy tutorials]. In fact, remember that | You can get more experience on using Yambopy for these kinds of visualization by following the [https://wiki.yambo-code.eu/wiki/index.php?title=First_steps_in_Yambopy Yambopy tutorials]. In fact, remember that these scripts and all the other Yambopy tutorial scripts are just suggestions, not source code written in stone: if you know <code>numpy</code> and <code>matplotlib</code> you can do your own analysis and your own plots, you just need to import the required Yambopy modules to load the data. | ||
In our case, the resulting plot is the following. | In our case, the resulting plot is the following. | ||
[[File:1L MoS2 | [[File:1L MoS2 MoS2 Ex-ph.png|500px|center]] | ||
This can be checked against Fig. 2(d) of reference <ref name="chan2023" />, although you have to keep in mind that our results are badly undersampled in terms of the reciprocal-space grid, as can be easily seen, and the quantity plotted is not exactly the same. However, the main features are already there since they are dictated mostly by crystal symmetries. | This can be checked against Fig. 2(d) of reference <ref name="chan2023" />, although you have to keep in mind that our results are badly undersampled in terms of the reciprocal-space grid, as can be easily seen, and the quantity plotted is not exactly the same. However, the main features are already there since they are dictated mostly by crystal symmetries. | ||
| Line 419: | Line 431: | ||
The signal from the phonon replicas can be modeled as a second-order scattering process involving one phonon and one photon: | The signal from the phonon replicas can be modeled as a second-order scattering process involving one phonon and one photon: | ||
<math>I^{ | <math>I^{Sat}(\omega)=\frac{1}{ N_q} \frac{1}{3} \sum_{\epsilon s\beta \mu q} \frac{1}{E_{\beta q}-s\Omega_{\mu q}}\left|\sum_\alpha\frac{ D^{\epsilon}_\alpha \mathcal{G}_{\beta \alpha}^{\mu,*}(q)}{E_\alpha -E_{\beta q} +s\Omega_{\mu q}+\mathrm{i}\eta}\right|^2 \frac{N^{exc}_{\beta q}(T_{exc})[\frac{1+s}{2}+n_{\mu q}(T)]}{\omega -[E_{\beta q}-s\Omega_{\mu q}]+\mathrm{i}\eta}</math> | ||
In this equation, the oscillator strength of the peak is given by the exciton-phonon coupling matrix elements <math>\mathcal{G}</math> multiplied by the exciton dipoles <math>D</math> (they are called "residuals" in Yambo). Here <math>E_\lambda</math> and <math>E_{\alpha q}</math> are the energies of the optical and finite-momentum excitons, respectively, while <math>\Omega_{\mu q}</math> are the phonon energies. | In this equation, the oscillator strength of the peak is given by the exciton-phonon coupling matrix elements <math>\mathcal{G}</math> multiplied by the exciton dipoles <math>D</math> (they are called "residuals" in Yambo). Here <math>E_\lambda</math> and <math>E_{\alpha q}</math> are the energies of the optical and finite-momentum excitons, respectively, while <math>\Omega_{\mu q}</math> are the phonon energies. | ||
Here, <math>n_{\mu q}(T)</math> is the temperature-dependent phonon Bose-Einstein occupation function. As it can be seen, <math>s=1</math> corresponds to processes of phonon ''emission'' (<math>\propto n(T)+1</math>), while <math>s=-1</math> corresponds to processes of phonon ''absorption'' (<math>\propto n(T)</math>). Therefore, <math>I^{Sat}_{PL}(\omega;T)</math> describes ''light'' emission by recombining excitons mediated by either ''phonon'' absorption or emission. | |||
The quantity <math> N_{\alpha q}(T_{exc})</math> is the exciton occupation function. Luminescence is technically an out-of-equilibrium process, but we can assume that for very low density of excitations and in steady-state conditions, the exciton population can be approximately described by an equilibrium distribution evaluated at an effective temperature. Here, we use the Boltzmann distribution. Experimentally, <math>T_{exc}</math> tends to coincide with the lattice temperature <math>T</math> more or less above 100 K, while at very low temperature (< 10 K), <math>T_{exc}</math> may vary between 10-50 K. It goes without saying that this needs to carefully be checked in your realistic calculations. | The quantity <math> N_{\alpha q}(T_{exc})</math> is the exciton occupation function. Luminescence is technically an out-of-equilibrium process, but we can assume that for very low density of excitations and in steady-state conditions, the exciton population can be approximately described by an equilibrium distribution evaluated at an effective temperature. Here, we use the Boltzmann distribution. Experimentally, <math>T_{exc}</math> tends to coincide with the lattice temperature <math>T</math> more or less above 100 K, while at very low temperature (< 10 K), <math>T_{exc}</math> may vary between 10-50 K. It goes without saying that this needs to carefully be checked in your realistic calculations. | ||
Finally, the spectrum is averaged over the polarization directions of the emitted photons (<math>\epsilon=x,y,z</math> representing the respective dipole components). | |||
=== Running the jobs === | === Running the jobs === | ||
| Line 575: | Line 589: | ||
DipApproach= "G-space v" # [DIP] [G-space v/R-space x/Covariant/Shifted grids] | DipApproach= "G-space v" # [DIP] [G-space v/R-space x/Covariant/Shifted grids] | ||
DipComputed= "R V P" # [DIP] [default R P V; extra P2 Spin Orb] | DipComputed= "R V P" # [DIP] [default R P V; extra P2 Spin Orb] | ||
BSENGexx= | BSENGexx= 30000 Ry # [BSK] Exchange components | ||
#ALLGexx # [BSS] Force the use use all RL vectors for the exchange part | #ALLGexx # [BSS] Force the use use all RL vectors for the exchange part | ||
BSENGBlk= | BSENGBlk= 9000 Ry # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] | ||
% KfnQP_E | % KfnQP_E | ||
1.25997 | 1.08816 | 1.12683 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim | 1.25997 | 1.08816 | 1.12683 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim | ||
| Line 612: | Line 626: | ||
mpirun -np 8 yambo -F bse_Lbar.in -J bse_Lbar,bse_Lfull -C bse_Lbar | mpirun -np 8 yambo -F bse_Lbar.in -J bse_Lbar,bse_Lfull -C bse_Lbar | ||
5. Now we run <code>lelphc</code> with yambopy to get the el-ph matrix elements: | 5. Now we run <code>lelphc</code> (with or without yambopy: in the latter case remember the option <code>-D</code>) to get the el-ph matrix elements, particularly the <code>ndb.elph</code> databases: | ||
yambopy l2y -ph path/of/dvscf/hbn.dvscf -b 7 10 -par 4 2 -D | |||
=== Luminescence calculation === | |||
6. And finally we calculate exciton-phonon matrix elements and the luminescence spectrum in one go using a python script importing the Yambopy exciton-phonon tools: in order to do this, we need to take a look at all the necessary input variables for the formula written above. | |||
We can start from the script <code>luminescence.py</code> available in <code>tutorials/exciton-phonon</code>. | |||
import numpy as np | |||
import matplotlib.pyplot as plt | |||
from yambopy.exciton_phonon.excph_luminescence import exc_ph_luminescence | |||
from yambopy.exciton_phonon.excph_input_data import exc_ph_get_inputs | |||
We import the necessary tools... | |||
path = '3D_hBN' | |||
<span style="color:blue"># Path to BSE calculation (Lout--> response is Lfull)</span> | |||
bsepath = f'{path}/bse_Lfull' <span style="color:blue"># ndb.BS_diago_Q* databases are needed</span> | |||
<span style="color:blue"># Path to BSE calculation for optically active exciton (Lin --> response is Lbar)</span> | |||
bseBARpath = f'{path}/bse_Lbar' <span style="color:blue"># ndb.BS_diago_Q1 database is needed</span> | |||
<span style="color:blue"># Path to electron-phonon calculation</span> | |||
elphpath = path <span style="color:blue"># ndb.elph is needed</span> | |||
<span style="color:blue"># Path to unprojected dipoles matrix elements (optional)</span> | |||
dipolespath = bsepath <span style="color:blue"># ndb.dipoles is needed (optional)</span> | |||
<span style="color:blue"># Path to lattice and k-space info</span> | |||
savepath = f'{path}/SAVE' <span style="color:blue"># ns.db1 database is needed</span> | |||
... and we specify the paths to the necessary databases. Note that, if we want to perform polarization averaging, we have to recompute the excitonic dipoles in python as seen here. | |||
What about <code>bseBARpath</code>? This variable points to the directory where the databases for the optical (zero-momentum) excitons <math>\alpha</math> (which may be computed with <code>Lkind='Lbar'</code>) is located, which can be different from the directory with the full indirect exciton dispersion <math>\beta</math> (usually computed with <code>Lkind='Lfull'</code>, however <code>Lkind='Ltilde'</code> can also be used if one is interested in "irreducible" excitons). This makes it possible to compute the coupling between different exciton kinds. | |||
bands_range=[6,10] <span style="color:blue"># 2 valence, 2 conduction bands</span> | |||
phonons_range=[0,12] <span style="color:blue"># All phonons</span> | |||
nexc_out = 12 <span style="color:blue"># 12 excitonic states at each momentum (Lout)</span> | |||
nexc_in = 12 <span style="color:blue"># 12 excitonic states at Q=0 (Lin)</span> | |||
T_ph = 10 <span style="color:blue"># Lattice temperature</span> | |||
T_exc = 10 <span style="color:blue"># Effective excitonic temperature</span> | |||
emin=4.4 <span style="color:blue"># Energy range and plot details (in eV)</span> | |||
emax=4.7 | |||
estep=0.0002 | |||
broad = 0.005 <span style="color:blue"># Broadening parameter for peak width (in eV)</span> | |||
Next, we specify the parameters for the calculation. We include valence bands from 7 to 10 (6 to 9 in python index) and the contribution of all 12 phonon modes. We consider 12 excitonic states for the coupling matrix elements. | |||
Here <code>T_ph</code> and <code>T_exc</code> are the lattice and excitonic temperatures, respectively. | |||
<span style="color:blue"># We calculate and load all the inputs:</span> | |||
<span style="color:blue"># * Exciton-phonon matrix elements</span> | |||
<span style="color: | <span style="color:blue"># * Excitonic dipole matrix elements</span> | ||
<span style="color: | <span style="color:blue"># * Exciton energies</span> | ||
<span style="color: | <span style="color:blue"># * Phonon energies</span> | ||
<span style="color:blue"># * We specify bse_path2=bseBARpath meaning we use Lbar calculation for Q=0 excitons</span> | |||
input_data = exc_ph_get_inputs(savepath,elphpath,bsepath,\ | |||
bse_path2=bseBARpath,dipoles_path=dipolespath,\ | |||
nexc_in=12,nexc_out=12,\ | |||
bands_range=[6,10],phonons_range=[0,12]) | |||
<span style="color:blue"># | |||
ph_energies, exc_energies, exc_energies_in, G, exc_dipoles = input_data | |||
The function <code>exc_ph_get_inputs</code> gives us all the input data for luminescence in the correct format: phonon energies, exciton energies, optical exciton energies (if needed), exciton-phonon matrix elements (calculated on the fly and printed to file), unprojected exciton dipoles (optional, calculated on the fly and printed to file). | |||
The exc-ph matrix element calculation is just a wrapper of the same tools that we have tested in the above section on MoS2. | |||
Finally, there is the calculation of the luminescence spectrum via the function <code>exc_ph_luminescence</code>: | |||
<span style="color:blue"># We calculate the luminescence spectrum including the input data from before</span> | |||
w,PL = exc_ph_luminescence(T_ph,ph_energies,exc_energies,exc_dipoles,G,\ | |||
exc_energies_in=exc_energies_in,exc_temp=T_exc,\ | |||
nexc_out=nexc_out,nexc_in=nexc_in,emin=emin,emax=emax,\ | |||
estep=estep,broad=broad) | |||
If you want to print the luminescence data for later plotting, you can also add the following line to the script: | |||
<span style="color:blue"># Save to file</span> | |||
data = np.column_stack((w, PL)) | |||
np.savetxt("hBN_luminescence_12x12x1.dat", data, fmt="%.8f") | |||
It is now time to run the whole script: | |||
python luminescence.py | |||
NB: By using Yambopy for Step 6, we have limited the use of the Yambo code to just step 4 in the entire workflow. This option is more flexible, as it allows for a greater degree of control by the user. On the other hand the Yambo postprocessing route features a Yambo-style input that doesn't require python knowledge and the calculation is currently faster in fortran. However, the luminescence expression computed in Yambo is a slightly different than this one: it is more approximated in the description of the satellite oscillator strengths, but it explicitly includes the renormalization of the direct exciton peak. You can check the differences [[Exciton-phonon coupling and luminescence - Yambo postprocessing|here]]. | |||
=== Results === | |||
We can plot the results of the step 6 calculation. If we do it in the same script we can add something like this: | |||
fig = plt.figure() | |||
ax = fig.add_subplot(1,1,1) | |||
ax.set_xlim(emin,emax) | |||
ax.set_ylim(0,np.max(PL)*1.1) | |||
ax.get_yaxis().set_visible(False) | |||
ax.plot(w, PL, '-',c='red', label="AA' hBN luminescence") | |||
plt.legend() | |||
plt.savefig('hBN_luminescence.png') | |||
plt.show() | |||
[[File: | [[File:HBN luminescence satellites.png|500px|center]] | ||
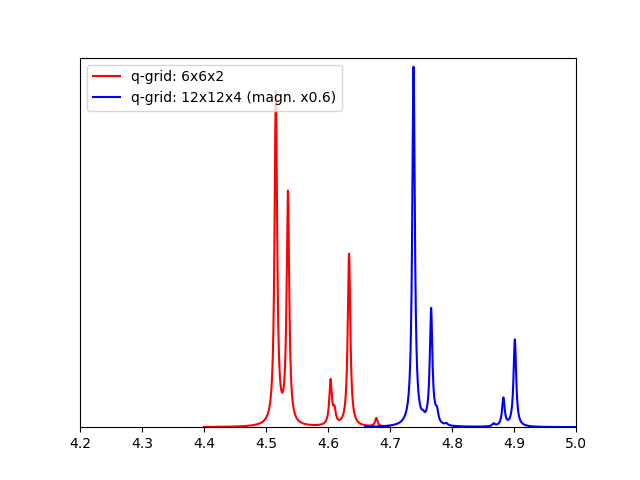
Here, the signal corresponds to a finite-momentum exciton that recombines with the help of several different phonon modes, both optical and acoustic. Each phonon mode whose coupling with the exciton is allowed can generate a peak, and the energy shifts of these peaks with respect to the initial exciton energy correspond to the phonon energies. This result is underconverged, but the main features are all there. In the plot, we show a more converged example using a 12x12x4 grid (all the other parameters being equal). These plots can be compared with Fig. 4(a) of reference <ref name="zanfrognini2023" />. | Here, the signal corresponds to a finite-momentum exciton that recombines with the help of several different phonon modes, both optical and acoustic. Each phonon mode whose coupling with the exciton is allowed can generate a peak, and the energy shifts of these peaks with respect to the initial exciton energy correspond to the phonon energies. This result is underconverged, but the main features are all there. In the plot, we show a more converged example using a 12x12x4 grid (all the other parameters being equal). These plots can be compared with Fig. 4(a) of reference <ref name="zanfrognini2023" />. | ||
| Line 670: | Line 731: | ||
<references> | <references> | ||
<ref name="toyozawa2003" >[https://m.booksee.org/book/1121964?force_lang= | <ref name="toyozawa2003" >Toyozawa, Yutaka, and Chris Oxlade, ''Optical processes in solids'', [https://m.booksee.org/book/1121964?force_lang=en Cambridge University Press, (2003)]. </ref> | ||
<ref name='lechifflart2023'>P. Lechifflart, F. Paleari, D. Sangalli, C. Attaccalite, ''First-principles study of luminescence in hexagonal boron nitride single layer: Exciton-phonon coupling and the role of substrate'', | <ref name='lechifflart2023'>P. Lechifflart, F. Paleari, D. Sangalli, C. Attaccalite, ''First-principles study of luminescence in hexagonal boron nitride single layer: Exciton-phonon coupling and the role of substrate'', | ||
[https://doi.org/10.1103/PhysRevMaterials.7.024006 Phys. Rev. M, '''7''' (2), 024006 (2023)]; [https://arxiv.org/abs/2212.10407 arXiv2212.1047]</ref> | [https://doi.org/10.1103/PhysRevMaterials.7.024006 Phys. Rev. M, '''7''' (2), 024006 (2023)]; [https://arxiv.org/abs/2212.10407 arXiv2212.1047]</ref> | ||
| Line 677: | Line 738: | ||
<ref name='chen2020'>''Exciton-Phonon Interaction and Relaxation Times from First Principles'', | <ref name='chen2020'>''Exciton-Phonon Interaction and Relaxation Times from First Principles'', | ||
Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, [https://doi.org/10.1103/PhysRevLett.125.107401 Phys. Rev. Lett. '''125''', 107401 (2020)]; [https://arxiv.org/abs/2002.08913 arXiv 2002.08913 (2020)]</ref> | Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, [https://doi.org/10.1103/PhysRevLett.125.107401 Phys. Rev. Lett. '''125''', 107401 (2020)]; [https://arxiv.org/abs/2002.08913 arXiv 2002.08913 (2020)]</ref> | ||
<ref name="lechifflart2023_PhD">[https://www.yambo-code.eu/wiki/images/5/54/These_final.pdf | <ref name="lechifflart2023_PhD">P. Lechifflart, ''Exciton-phonon coupling and phonon-assisted luminescence in hexagonal Boron Nitride nanostructures'', [https://hal.science/tel-04266805v1 PhD Thesis, University of Marseille (2023)]; [https://www.yambo-code.eu/wiki/images/5/54/These_final.pdf From the yambo website]</ref> | ||
<ref name='paleari2019_PhD'>F. Paleari, ''First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride'', [https://wwwen.uni.lu/research/fstm/dphyms/people/fulvio_paleari PhD thesis, University of Luxembourg (2019)]</ref> | <ref name='paleari2019_PhD'>F. Paleari, ''First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride'', [https://wwwen.uni.lu/research/fstm/dphyms/people/fulvio_paleari PhD thesis, University of Luxembourg (2019)]</ref> | ||
<ref name='zanfrognini2023'> | <ref name='zanfrognini2023'>M. Zanfrognini et al., ''Distinguishing different stackings in layered materials via luminescence spectroscopy'', [https://doi.org/10.1103/PhysRevLett.131.206902 Phys. Rev. Lett. '''131''', 206902 (2023)]; [https://arxiv.org/abs/2305.17554 arXiv 2305.17554] </ref> | ||
<ref name='marini2024'>G. Marini, M. Calandra, P. Cudazzo, ''Optical absorption and photoluminescence of single layer boron nitride from a first principles cumulant approach'', [https://doi.org/10.1021/acs.nanolett.4c00669 Nano Lett., '''24''', 20, 6017 (2024)]; [https://arxiv.org/abs/2402.03826 arXiv 2402.03826 (2024)]</ref> | <ref name='marini2024'>G. Marini, M. Calandra, P. Cudazzo, ''Optical absorption and photoluminescence of single layer boron nitride from a first principles cumulant approach'', [https://doi.org/10.1021/acs.nanolett.4c00669 Nano Lett., '''24''', 20, 6017 (2024)]; [https://arxiv.org/abs/2402.03826 arXiv 2402.03826 (2024)]</ref> | ||
<ref name='antonius2017'>G. Antonius, S. G. Louie, ''Theory of exciton-phonon coupling'', [https://doi.org/10.1103/PhysRevB.105.085111 Phys. Rev. B, '''105''', 085111 (2022)]; [https://arxiv.org/abs/1705.04245 arXiv1705.04245 (2017)]</ref> | <ref name='antonius2017'>G. Antonius, S. G. Louie, ''Theory of exciton-phonon coupling'', [https://doi.org/10.1103/PhysRevB.105.085111 Phys. Rev. B, '''105''', 085111 (2022)]; [https://arxiv.org/abs/1705.04245 arXiv1705.04245 (2017)]</ref> | ||
<ref name='paleari2022'> | <ref name='paleari2022'> F. Paleari, and A. Marini, ''Exciton-phonon interaction calls for a revision of the “exciton” concept'', [https://doi.org/10.1103/PhysRevB.106.125403 Phys. Rev. B, '''106''', 125403 (2022)]; [https://arxiv.org/abs/2205.02783 arXiv 2205.02783]</ref> | ||
<ref name='cudazzo2020'> P. Cudazzo, ''First-principles description of the exciton-phonon interaction: A cumulant approach'', [https://doi.org/10.1103/PhysRevB.102.045136 Phys. Rev. B, '''102''', 045136 (2020)]; [https://orbilu.uni.lu/bitstream/10993/44769/1/main.pdf Open access pdf from Luxembourg University]</ref> | <ref name='cudazzo2020'> P. Cudazzo, ''First-principles description of the exciton-phonon interaction: A cumulant approach'', [https://doi.org/10.1103/PhysRevB.102.045136 Phys. Rev. B, '''102''', 045136 (2020)]; [https://orbilu.uni.lu/bitstream/10993/44769/1/main.pdf Open access pdf from Luxembourg University]</ref> | ||
<ref name='chan2023'>Y-h Chan, J. B. Haber, M. H. Naik, J. B. Neaton, D. Y. Qiu, F. H. da Jornada, S. G. Louie, ''Exciton Lifetime and Optical Line Width Profile via Exciton–Phonon Interactions: Theory and First-Principles Calculations for Monolayer MoS2'', [https://doi.org/10.1021/acs.nanolett.3c00732 Nano Lett., '''23''', 9 (2023)]; [https://arxiv.org/abs/2212.08451 arXiv 2212.08451 (2023)]</ref> | <ref name='chan2023'>Y-h Chan, J. B. Haber, M. H. Naik, J. B. Neaton, D. Y. Qiu, F. H. da Jornada, S. G. Louie, ''Exciton Lifetime and Optical Line Width Profile via Exciton–Phonon Interactions: Theory and First-Principles Calculations for Monolayer MoS2'', [https://doi.org/10.1021/acs.nanolett.3c00732 Nano Lett., '''23''', 9 (2023)]; [https://arxiv.org/abs/2212.08451 arXiv 2212.08451 (2023)]</ref> | ||
<ref name='murali2025'>M. Nalabothula, S. Reichardt, L. Wirtz, ''Origin of Interlayer Exciton–Phonon Coupling in 2D Heterostructures'', [https://doi.org/10.1021/acs.nanolett.5c00355 Nano Lett., '''25''', 15 (2025)], [https://arxiv.org/abs/2407.16111 arXiv 2407.16111 (2025)]</ref> | <ref name='murali2025'>M. Nalabothula, S. Reichardt, L. Wirtz, ''Origin of Interlayer Exciton–Phonon Coupling in 2D Heterostructures'', [https://doi.org/10.1021/acs.nanolett.5c00355 Nano Lett., '''25''', 15 (2025)], [https://arxiv.org/abs/2407.16111 arXiv 2407.16111 (2025)]</ref> | ||
</references> | </references> | ||
Latest revision as of 10:54, 20 November 2025
In this advanced tutorial, we will calculate exciton-phonon interactions from first principles by interfacing DFPT (for phonon calculations) and BSE (for exciton calculations).
The DFTP calculations are run with Quantum ESPRESSO, while the many-body GW-BSE calculations are run with Yambo. Finally, the exciton-phonon interaction will be obtained by combining and postprocessing the databases computed in the two previous runs. The great advantage of this workflow is that the calculations can be run in the irreducible Brillouin zones both for the electronic momenta (k) and the transfer momenta (Q, q) of excitons and phonons, thus speeding up considerably the jobs while reducing the IO and memory load.
We will first compute the exciton-phonon coupling matrix elements: these are the building blocks needed to construct experimental observables such as phonon-assisted optical spectra (such as luminescence), Raman spectra and exciton lifetimes. We will do this in the case of monolayer MoS2, a 2D system with large spin-orbit interaction.
As an example of application, we will consider the case of phonon-assisted luminescence. We will do this in the case of bulk hBN, a layered indirect insulator with strong electron-phonon coupling.
Note: this tutorial will be updated when new exc-ph tools become available in Yambopy (including full-python postprocessing, Raman spectra, interpolated lifetimes, etc).
Requirements
This is an advanced topic: we assume that you already know something about the theory[1][2][3][4][5][6] and applications[7][8][9][10][11][12][13][14] of exciton-phonon physics.
Also, we assume that you already know how to run both a basic Yambo GW-BSE calculation and a DFPT phonon calculation with Quantum ESPRESSO.
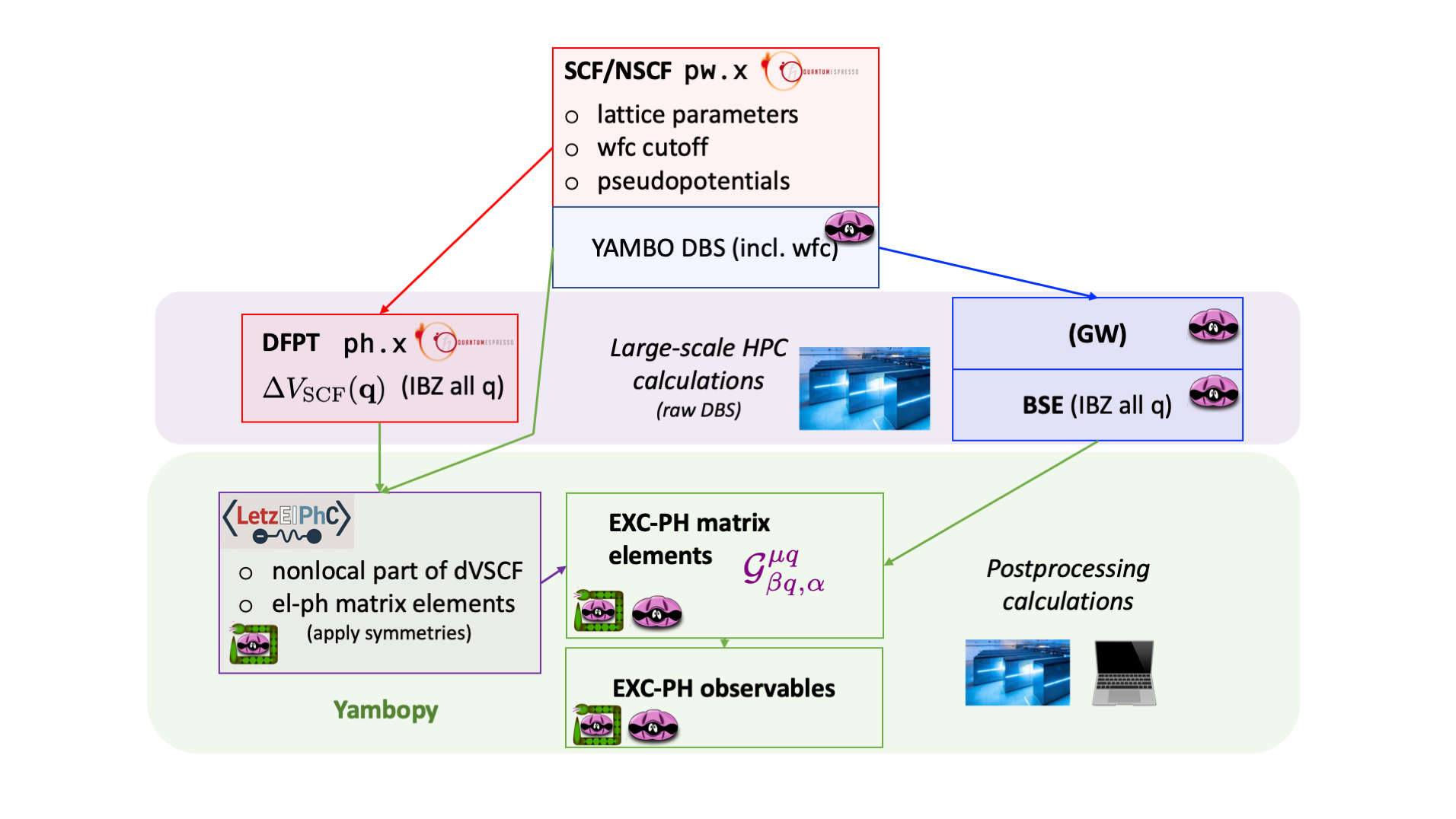
Besides the QE executables pw.x and ph.x, we also use the yambo phonon-specific executable yambo_ph and the python utility Yambopy. The auxiliary code LetzElPhC (executable lelphc) will be used to obtain the electron-phonon matrix elements by reading the same electronic wavefunctions used by Yambo (and stored in the SAVE directory), while also making full use of crystal symmetries. LetzElPhC will be run by Yambopy, but it must nonetheless be installed. Finally, the exciton-phonon properties can be computed either using yambo_ph or using Yambopy itself. Both cases will be covered in this tutorial.
Step 0: Pseudopotentials, equilibrium structure and convergence
In a real calculation, it is important to ensure that both the pseudopotential and the lattice parameters that we are using are compatible and perform well for the electronic excited states and for the lattice vibrations simultaneously. Furthermore, you have to make sure that the wave function cutoff ecutwfc is converged with respect to the DFPT step and not just to the DFT one. This is in addition to the other customary convergence tests for DFT, DFPT, GW and BSE calculations.
This is often the most time-demanding step when starting on a new system.
For the sake of this tutorial, we assume that we have already done all these tests and we are starting the final workflow to get the exciton-phonon properties.
Step 1: scf calculation
First of all, we run a standard scf calculation with pw.x for Yambo. We stick with non-symmorphic symmetries. At the end, we will have the QE save directory.
This is the input mos2.scf:
&control
wf_collect = .true.,
calculation = "scf",
verbosity = 'high',
pseudo_dir = '$PSEUDO_DIR',
prefix = "mos2",
outdir = '.',
/&end
&system
ecutwfc = 100.0,
occupations = 'fixed',
ibrav = 4,
celldm(1) = 5.9000811881,
celldm(3) = 6.7795677253,
nat = 3,
ntyp = 2,
lspinorb = .true.
noncolin = .true.
assume_isolated = '2D'
force_symmorphic = .true.
/&end
&electrons
electron_maxstep = 200,
mixing_beta = 0.7,
conv_thr = 1.d-08,
/&end
ATOMIC_SPECIES
Mo 95.940 Mo_ONCV_PBE_FR-1.0.upf
S 32.065 S_ONCV_PBE_FR-1.1.upf
ATOMIC_POSITIONS { crystal }
Mo 0.333333333 0.666666667 0.000000000
S 0.666666667 0.333333333 0.073413577
S 0.666666667 0.333333333 -0.073413577
K_POINTS { automatic }
6 6 1 0 0 0
Here we are using full relativistic pseudopotentials from the SG-15 database.
We can run it on our machine (for example using 4 MPI tasks) as:
mpirun -np 4 pw.x -inp mos2.scf > scf.out
Step 2: nscf calculation for Yambo
Copy the QE save directory from the scf calculation and run the nscf calculation for any number of empty states, with the correct k-grid we want to use in Yambo. Here we are using a badly underconverged grid of 6x6x1.
This reciprocal-space grid will also match the momentum transfer q grid on which excitons and phonons will be defined!
The electronic wavefunctions computed at this step and stored in the new nscf save directory will be used both by Yambo and by the electron-phonon code: this is important because using different sets of wavefunctions would lead to a phase mismatch issue in the exciton-phonon matrix elements.
The nscf input mos2.nscf is
&control
wf_collect = .true.,
calculation = "nscf",
verbosity = 'high',
pseudo_dir = '$PSEUDO_DIR',
prefix = "mos2",
outdir = '.',
/&end
&system
ecutwfc = 100.0,
occupations = 'fixed',
ibrav = 4,
celldm(1) = 5.9000811881,
celldm(3) = 6.7795677253,
nat = 3,
ntyp = 2,
lspinorb = .true.
noncolin = .true.
nbnd = 250
assume_isolated = '2D'
force_symmorphic = .true.
/&end
&electrons
electron_maxstep = 200,
mixing_beta = 0.7,
conv_thr = 1.d-08,
/&end
ATOMIC_SPECIES
Mo 95.940 Mo_ONCV_PBE_FR-1.0.upf
S 32.065 S_ONCV_PBE_FR-1.1.upf
ATOMIC_POSITIONS { crystal }
Mo 0.333333333 0.666666667 0.000000000
S 0.666666667 0.333333333 0.073413577
S 0.666666667 0.333333333 -0.073413577
K_POINTS { automatic }
6 6 1 0 0 0
Again, we run the calculation
mpirun -np 4 pw.x -inp mos2.nscf > nscf.out
Step 3: dvscf phonon calculation
Now we run the phonon calculation.
Copy the save directory from the scf calculation and run ph.x for a dvscf calculation with a standard q-grid matching the k-grid we wanna use in Yambo.
At the end, we will have the _ph0 directory containing the variation of the self-consistent potential, [math]\displaystyle{ \Delta V_{SCF}(q) }[/math], and the *.dyn files with the phonon energies and eigenvectors.
NB: one could further refine the phonon energies by enforcing the acoustic sum rule, including non-analytic long-range contributions, interpolating to finer grids... all of this can be done within Quantum ESPRESSO and will not be covered in this version of the tutorial.
The input is mos2.dvscf:
mos2_dvscf &inputph tr2_ph=1.0d-12, verbosity='high' prefix='mos2', fildvscf = 'mos2-dvscf', electron_phonon = 'dvscf', fildyn='mos2.dyn', epsil=.false., ldisp=.true., recover=.true., nq1=6, nq2=6, nq3=1 /
And now we run as
nohup mpirun -np 8 ph.x -inp mos2.dvscf > dvscf.out &
This time we use nohup and more processes because this calculation may take some time. It is a good idea to set recover=.true. as in a real calculation you will easily breach walltime, and in this way you can safely restart.
Step 4: create Yambo SAVE directory
This is just the standard Yambo initialization: run
p2y
and then
yambo
in the nscf save folder and then move the newly generated SAVE directory to a convenient place.
Step 5: run a BSE calculation
Now we switch from QE to Yambo. Here, we forgo the GW step for simplicity (we can use a scissor operator to open the band gap).
This calculation has a couple of differences with respect to a standard BSE calculation for optical absorption. We can look at the input file bse.in:
# Runlevels optics # [R OPT] Optics rim_cut # [R RIM CUT] Coulomb potential bss # [R BSS] Bethe Salpeter Equation solver em1s # [R Xs] Static Inverse Dielectric Matrix bse # [R BSE] Bethe Salpeter Equation. bsk # [R BSK] Bethe Salpeter Equation kernel # RIM and cutoff settings RandQpts=1000000 # [RIM] Number of random q-points in the BZ RandGvec= 100 RL # [RIM] Coulomb interaction RS components CUTGeo= "slab z" # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY.. # Static screening X_and_IO_CPU= "1 1 4 2 1" # [PARALLEL] CPUs for each role X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v) X_and_IO_nCPU_LinAlg_INV=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) Chimod= "hartree" # [X] IP/Hartree/ALDA/LRC/BSfxc % BndsRnXs 1 | 200 | # [Xs] Polarization function bands % % LongDrXs 1.000000 | 1.000000 | 1.000000 | # [Xs] [cc] Electric Field % NGsBlkXs= 8000 mRy # [Xs] Response block size # BSE BS_CPU= "4.1.2" # [PARALLEL] CPUs for each role BS_ROLEs= "k.eh.t" # [PARALLEL] CPUs roles (k,eh,t) BS_nCPU_diago=4 # [PARALLEL] CPUs for matrix diagonalization BSEmod= "causal" # [BSE] resonant/causal/coupling BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` BSENGexx= 40000 mRy # [BSK] Exchange components ALLGexx # [BSS] Force the use use all RL vectors for the exchange part BSENGBlk= 8000 mRy # [BSK] Screened interaction block size Lkind="full" #[BSE,X] bar(default)/full/tilde % KfnQP_E 1.000000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % % BEnRange 0.00000 | 4.00000 | eV # [BSS] Energy range % % BDmRange 0.05000 | 0.05000 | eV # [BSS] Damping range % BEnSteps= 2000 # [BSS] Energy steps % BLongDir 1.000000 | 0.000000 | 0.000000 | # [BSS] [cc] Electric Field % % BSEQptR 1 | 7 | # [BSK] Transferred momenta range % % BSEBands 25 | 28 | # [BSK] Bands range % WRbsWF # [BSS] Write to disk excitonic the FWs
This file was generated using the command: yambo -X s -o b -k sex -y d -r
First of all, we compute the excitons for all the momenta in the irreducible Brillouin zone for our discrete grid via the BSEQptR variable. This will be a finite-momentum BSE calculation, analogous to the phonon one.
Second, we change the variable Lkind from bar to full. In Yambo, Lkind="bar", which is the default for optical absorption, means that we are computing the excitonic response function without the long-range component of the exchange interaction. This cannot be used when computing the exciton momentum dependence, where the long-range exchange interaction can play a role, therefore we have to include it with Lkind="full". This allows for the calculation of the excitonic longitudinal-transverse splitting (in 3D systems) as well.
We can now run the code:
nohup mpirun -np 8 yambo -F bse.in -J bse_Lfull -C bse_Lfull &
At the end of the calculation, we have obtained the ndb.BS_diago_Q* databases inside the directory bse_Lfull. They contain information on the exciton energies and wavefunctions at each momentum. Do not forget to check the report and logs of your calculation in the same directory to make sure that the code is doing what you want.
Step 6: obtain the electron-phonon matrix elements
We have finished the heavy simulations. Now it's time for the postprocessing. The first order of business is the reconstruction of the electron-phonon coupling matrix elements from the dvscf results and the electronic wavefunctions.
In order to do this, we will run the lelphc executable of the LetzElPhC code. We will run via command line using yambopy, although it will be instructive to have look at the lelphc input files later.
We run in the same directory where the Yambo SAVE is (remember than you can also virtually move it with a symbolic link).
Type:
yambopy l2y
to see the help for the calculation. Have a look at the various flags and their description. For example, if we want to do a serial run of LetzElPhC for bands from [math]\displaystyle{ n_i }[/math] to [math]\displaystyle{ n_f }[/math], we should type:
yambopy l2y -ph path/of/ph_input.in -b n_i n_f
Here [math]\displaystyle{ n_i }[/math] and [math]\displaystyle{ n_f }[/math] are integers representing the initial and final band indices. Please note: in this case, the band index starts from 1 and the the interval of bands read by the code is [math]\displaystyle{ [n_i,n_f] }[/math] including the extrema of the interval.
These should coincide with those used for the Bethe-Salpeter kernel, i.e. those specified in the BSEBands variable of the BSE input file (this is not strictly necessary, but certainly efficient since these calculations use a lot of disk space).
For our system, we want to do a parallel calculation with 4 qpools and 2 kpools. In addition, we want to explicitly specify the path of the lelphc executable and avoid automatically deleting the LetzElPhC data. So we type:
yambopy l2y -ph path/of/dvscf/mos2.dvscf -b 25 28 -par 4 2 -lelphc path/to/lelphc_exe
At the end, check your directory: you should find the lelphc.in input file that was run, let's inspect it:
# LetzElPhC input for yambo generated by yambopy nqpool = 2 nkpool = 4 start_bnd = 25 end_bnd = 28 save_dir = ./SAVE kernel = dfpt ph_save_dir = dvscf/ph_save convention = yambo
Notice the variable convention=yambo: what does it mean? At variance with QE and many other codes, Yambo uses the "backward" momentum transfer convention for electronic scatterings. That is, an electronic transition goes from band [math]\displaystyle{ n }[/math] and momentum [math]\displaystyle{ k-q }[/math] to band [math]\displaystyle{ m }[/math] and momentum [math]\displaystyle{ k }[/math]. In the "forward" momentum transfer convention (the more standard one), the transitions go from [math]\displaystyle{ nk }[/math] to [math]\displaystyle{ mk+q }[/math]. Therefore, this variable ensures that the electron-phonon coupling matrix elements are computed as [math]\displaystyle{ \langle mk|dV|nk-q\rangle }[/math]. This will have consequences also in the formulation of the exciton-phonon coupling matrix element.
You will also find a ndb.elph database that contains the computed electron-phonon matrix elements, in the output format of LetzElPhC.
In addition, if you check the SAVE folder:
ls SAVE/ndb.elph_gkkp*
you will see that yambopy has created the Yambo-compatible electron-phonon databases.
If you want to run LetzElPhC directly, without using yambopy, you can refer to its [guide].
Keep in mind that in this case, in order to convert the database to the ndb.elph_gkkp* databases of Yambo, you will then need a couple of lines of python using the Yambopy class ConvertElectronPhononDB in yambopy/letzelph_interface/lelph2y.py.
If you don't need the ndb.elph_gkkp* databases -- e.g., because you are doing the exc-ph postprocessing with yambopy -- you can run yambopy l2y ... with the --no_gkkp option.
If you don't need the ndb.elph databases -- e.g., because you are using yambo_ph for the exc-ph part -- you can run yambopy l2y ... with the --no_lelphc_dbs option.
Step 7: Obtain the exciton-phonon coupling
Now, we can finally access our basic building block for exciton-phonon physics. This could be done entirely in python (using Yambopy), or by running Yambo.
- For the Yambo postprocessing case (running yambo inputs with the
yambo_phexecutable), follow the alternative route to Steps 7-8 at this link. - For the Yambopy postprocessing case (using flexible python scripting), keep following Steps 7-8 on this page.
Our objective is obtaining the following quantity:
[math]\displaystyle{ \mathcal{G}^\mu_{\alpha\lambda}(0,q)=\sum_{vv^\prime c k} A^{\alpha, *}_{cv^\prime} (k, q) g_{vv^\prime}^\mu (k,q) A^{\lambda}_{cv}(k,0) - \sum_{cc^\prime vk} A^{\alpha, *}_{c^\prime v} (k+q, q) g_{c^\prime c}^\mu (k+q,q) A^{\lambda}_{cv}(k, 0) }[/math]
Here, [math]\displaystyle{ A^{\alpha}_{cv}(k,q) }[/math] are the exciton coefficients extracted from the eigenvector of the two-particles Hamiltonian during the BSE calculation in step 5, while [math]\displaystyle{ g_{nm}^\mu (k,q) }[/math] are the electron-phonon coupling matrix elements obtained in step 6. As you can see, the exciton [math]\displaystyle{ \lambda }[/math] undergoes phonon-mediated scattering to state [math]\displaystyle{ \alpha }[/math] via phonon mode [math]\displaystyle{ \mu }[/math]. The scattering can happen for the hole (valence, [math]\displaystyle{ v }[/math]) or for the electron (conduction, [math]\displaystyle{ c }[/math]).
NB:
(1) This is written in the "backward" momentum transfer convention used by Yambo. The momentum dependence is different in the "forward" transfer convention.
(2) For simplicity, this is written for zero initial exciton momentum. This means that one of the two states involved in the phonon-mediated scattering process will be in the optical limit (and possibly an optically generated exciton), while the other state can have any momentum: this momentum will be the same as the phonon one. This matrix element can be used to describe phonon-assisted absorption and emission spectra.
In order to calculate this quantity using python, we need the ndb.elph databases natively generated by the LetzElPhC code, as well as the BSE databases ndb.BS_diago_Q* containing the information on exciton wavefunctions and energies.
Next, we write a python user script importing the yambopy exciton-phonon tools. You can find a version of this script in yambopy/tutorials/exciton-phonon/calculate_excph.py.
import numpy as np from yambopy import YamboLatticeDB,YamboWFDB,LetzElphElectronPhononDB #Specific Yambopy dbs loading classes from yambopy.exciton_phonon.excph_matrix_elements import exciton_phonon_matelem #Specific exc-ph functions
path = '1L_MoS2' bands_range=[24,28] # 2 valence bands, 2 conduction bands nexc = 12 # number of excitonic states bsepath = f'{path}/bse-allq_full' # Path to BSE calculation (Lin=Lout) savepath = f'{path}/SAVE' # Yambo SAVE ndb_elph = f'{path}/ndb.elph' # LetzElPhC electron-phonon database (any convention)
# Read lattice lattice = YamboLatticeDB.from_db_file(filename=f'{savepath}/ns.db1') # Read electron-phonon elph = LetzElphElectronPhononDB(ndb_elph,read_all=False) # Read wave functions wfcs = YamboWFDB(filename='ns.wf',save=savepath,latdb=lattice,bands_range=bands_range) # Calculate exciton-phonon matrix elements exph = exciton_phonon_matelem(lattice,elph,wfcs,BSE_dir=bsepath,neigs=nexc,dmat_mode='save',exph_file='MoS2_Ex-ph.npy')
In this script, we can select the number exciton states [math]\displaystyle{ \lambda }[/math] with nexc, the single-particle bands range with bands_range. Please note: in this case, the band index starts from 0 (python indexing) and the the interval of bands read by the code is [math]\displaystyle{ [n_i,n_f) }[/math], therefore the last value (28 in the example) is excluded. That is, in the example we are selecting the 25th, 26th, 27th and 28th bands. Those bands have to be present in both the electron-phonon and BSE calculations.
Here we calculate the couplings of the first twelve states at each finite-[math]\displaystyle{ q }[/math] point including [math]\displaystyle{ q=0 }[/math]. We also include all the nine phonon modes of monolayer MoS2. We also need access to the Yambo SAVE directory in order to read the electronic wavefunctions: they are used to compute the electronic representation matrices (dmat in the code). The argument dmat_mode can be set to 'load' for subsequent calculations.
When we are satisfied with the input, we run the code:
python calculate_excph.py
If you check the output, you should find the MoS2_Ex-ph.npy binary file in the directory where you ran.
Analysis of the couplings
It is a good idea to have a look at what we computed up to now in order to make sure nothing has gone wrong.
It is not easy to know what to expect (apart from symmetry and gauge compliance of the matrix elements), but one can work out the exciton-phonon selection rules in advance, check that the magnitude is reasonable, etc.
It is also not easy to meaningfully plot this quantity. We have to make sure that we are not breaking degenerate states, otherwise the plots will not be invariant.
First of all, we have to know our system: in monolayer MoS2, the first four excitons are all doubly degenerate. The first exciton responsible for a bright peak in the absorption spectrum (the A peak), is the second state, corresponding to state indices (3,4) in fortran indexing or (2,3) in python indexing.
All these information can be obtained by analyzing the BSE results (this stuff is explained in the BSE tutorials) and by knowledge of the system or class of systems from the literature.
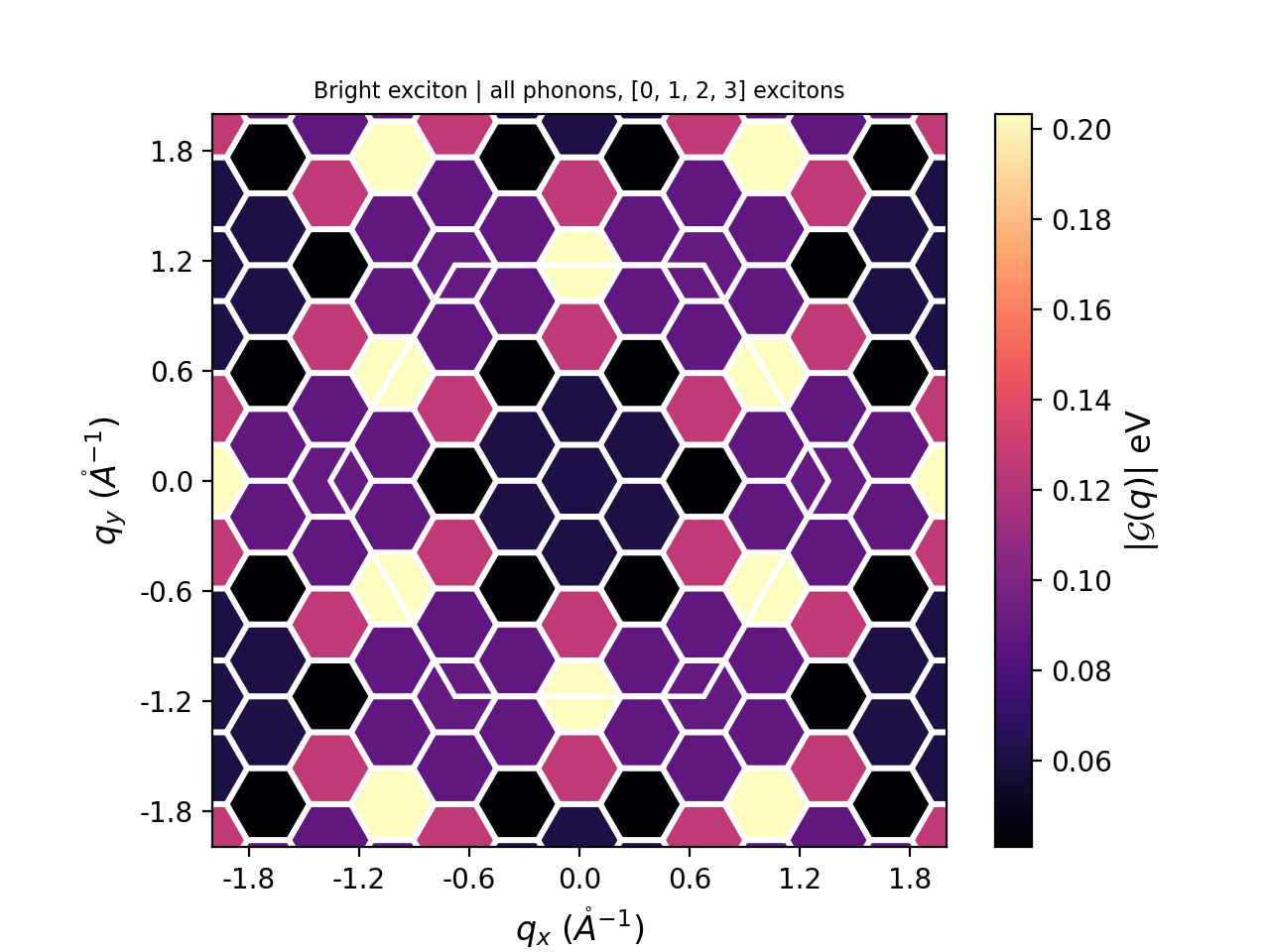
Thus, a good quantity to plot may be the norm of the matrix elements, summed over the degenerate subspace of exciton A, for a certain number of scattered final states mediated by certain phonon modes:
[math]\displaystyle{ F_A(q)= \sqrt{ \sum_{\alpha \in A,\lambda,\mu} |\mathcal{G}_{\alpha\lambda}^\mu (0,q)|^2 } }[/math]
In order to do this, we create a python script analyse_excph.py in which we first load the excph dabatases.
You can find a version of this script in the yambopy directory, in tutorials/exciton-phonon.
First, we select the exciton and phonon states to be included in F_A, together with the path of databases and plot details:
# Exciton "in" states exc_in = [2,3] # First bright peak (A: 2,3 -- B: 6,7) exc_out = [0,1,2,3] # first 4 states (dispersion of dark triplet state and A) ph_in = 'all' # Paths of databases ns_db1 =f'{path}/SAVE/ns.db1' ns_ypy = 'MoS2_Ex-ph.npy' ...
Then, we load the data:
# Read lattice and k-space info ylat = YamboLatticeDB.from_db_file(filename=ns_db1) print(ylat) # Load exc-ph database X_py = np.load(ns_ypy) G_squared = np.abs(X_py)**2.
The quantity [math]\displaystyle{ F_A(q) }[/math] is obtained from a dedicated function as:
if exc_in == 'all': exc_in = range(G_squared.shape[2])
if exc_out == 'all': exc_out = range(G_squared.shape[3])
if ph_in == 'all': ph_in = range(G_squared.shape[1])
G_squared = G_squared[:, ph_in, :, :].sum(axis=(1))
G_squared = G_squared[:, exc_in, :].sum(axis=(1))
G_squared = G_squared[:, exc_out].sum(axis=(1))
F_q = np.sqrt( G_squared )*ha2ev # Switch from Ha to eV
And finally, we have to make a plotting function. For this tutorial we will use a custom scatterplot employing some of the plotting tools provided by yambopy (but you can do whatever you want).
plot_2D_excph(qgrid,G2_to_plot,rlat=ylat.rlat,plt_cbar=True,\
marker='H',s=700,cmap='magma')
...
You can get more experience on using Yambopy for these kinds of visualization by following the Yambopy tutorials. In fact, remember that these scripts and all the other Yambopy tutorial scripts are just suggestions, not source code written in stone: if you know numpy and matplotlib you can do your own analysis and your own plots, you just need to import the required Yambopy modules to load the data.
In our case, the resulting plot is the following.
This can be checked against Fig. 2(d) of reference [12], although you have to keep in mind that our results are badly undersampled in terms of the reciprocal-space grid, as can be easily seen, and the quantity plotted is not exactly the same. However, the main features are already there since they are dictated mostly by crystal symmetries.
Now that we have the exciton-phonon matrix elements, we can use them to build several kinds of observables. Below, we give an example related to phonon-assisted luminescence, but we may update this tutorial in the future to include more cases.
Step 8: Compute phonon-assisted luminescence
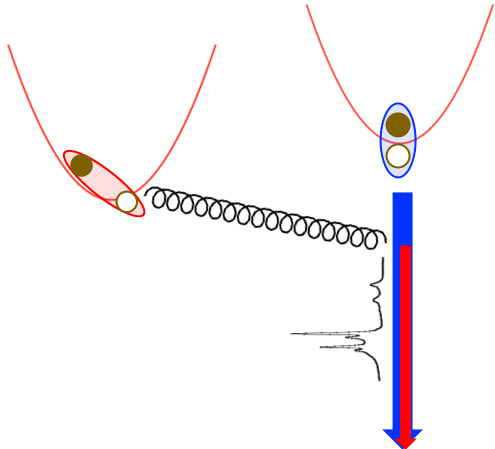
We want to compute the experimental optical signature due to the phonon-assisted recombination of an exciton (as sketched in the figure).
The signal from the phonon replicas can be modeled as a second-order scattering process involving one phonon and one photon:
[math]\displaystyle{ I^{Sat}(\omega)=\frac{1}{ N_q} \frac{1}{3} \sum_{\epsilon s\beta \mu q} \frac{1}{E_{\beta q}-s\Omega_{\mu q}}\left|\sum_\alpha\frac{ D^{\epsilon}_\alpha \mathcal{G}_{\beta \alpha}^{\mu,*}(q)}{E_\alpha -E_{\beta q} +s\Omega_{\mu q}+\mathrm{i}\eta}\right|^2 \frac{N^{exc}_{\beta q}(T_{exc})[\frac{1+s}{2}+n_{\mu q}(T)]}{\omega -[E_{\beta q}-s\Omega_{\mu q}]+\mathrm{i}\eta} }[/math]
In this equation, the oscillator strength of the peak is given by the exciton-phonon coupling matrix elements [math]\displaystyle{ \mathcal{G} }[/math] multiplied by the exciton dipoles [math]\displaystyle{ D }[/math] (they are called "residuals" in Yambo). Here [math]\displaystyle{ E_\lambda }[/math] and [math]\displaystyle{ E_{\alpha q} }[/math] are the energies of the optical and finite-momentum excitons, respectively, while [math]\displaystyle{ \Omega_{\mu q} }[/math] are the phonon energies.
Here, [math]\displaystyle{ n_{\mu q}(T) }[/math] is the temperature-dependent phonon Bose-Einstein occupation function. As it can be seen, [math]\displaystyle{ s=1 }[/math] corresponds to processes of phonon emission ([math]\displaystyle{ \propto n(T)+1 }[/math]), while [math]\displaystyle{ s=-1 }[/math] corresponds to processes of phonon absorption ([math]\displaystyle{ \propto n(T) }[/math]). Therefore, [math]\displaystyle{ I^{Sat}_{PL}(\omega;T) }[/math] describes light emission by recombining excitons mediated by either phonon absorption or emission.
The quantity [math]\displaystyle{ N_{\alpha q}(T_{exc}) }[/math] is the exciton occupation function. Luminescence is technically an out-of-equilibrium process, but we can assume that for very low density of excitations and in steady-state conditions, the exciton population can be approximately described by an equilibrium distribution evaluated at an effective temperature. Here, we use the Boltzmann distribution. Experimentally, [math]\displaystyle{ T_{exc} }[/math] tends to coincide with the lattice temperature [math]\displaystyle{ T }[/math] more or less above 100 K, while at very low temperature (< 10 K), [math]\displaystyle{ T_{exc} }[/math] may vary between 10-50 K. It goes without saying that this needs to carefully be checked in your realistic calculations.
Finally, the spectrum is averaged over the polarization directions of the emitted photons ([math]\displaystyle{ \epsilon=x,y,z }[/math] representing the respective dipole components).
Running the jobs
In order to study luminescence in a paradigmatic system, we switch to bulk hexagonal boron nitride and we repeat the workflow. As you can easily see, one can think about automatizing the execution of all these calculations via scripting or more advanced tools. However, in the case of very large simulations (memory-limited or disk-space limited) or for systems whose electronic and lattice properties are fragile with respect to tiny calculation details, one must be very careful and run many basic tests.
Fortunately, we are running a fast underconverged example. We use LDA pseudopotentials from the pseudo-dojo library and the following are the calculations steps.
1. Input hbn.scf:
&control
calculation='scf',
prefix='hBN',
restart_mode='from_scratch'
pseudo_dir = '$PSEUDO_DIR',
outdir = './tmp'
verbosity = 'high'
wf_collect=.true.
/
&system
ibrav = 4,
celldm(1) = 4.703675849
celldm(3) = 2.603711434
nat= 4,
ntyp= 2,
force_symmorphic=.true.
ecutwfc = 100,
/
&electrons
diago_david_ndim = 2
diago_full_acc=.true.
diago_thr_init=5.0e-6
mixing_mode = 'plain'
mixing_beta = 0.7
conv_thr = 1.0d-16
/
ATOMIC_SPECIES
B 10.81100 B_LDA_dojo.UPF
N 14.00674 N_LDA_dojo.UPF
ATOMIC_POSITIONS {crystal}
N 0.6666666670 0.3333333330 -0.250000000000
B 0.3333333330 0.6666666670 -0.250000000000
B 0.6666666670 0.3333333330 0.25000000000
N 0.3333333330 0.6666666670 0.25000000000
K_POINTS {automatic}
6 6 2 0 0 0
mpirun -np 4 pw.x -inp hbn.scf > scf.out
2. Input hbn.nscf:
&control
calculation='nscf',
prefix='hBN',
restart_mode='from_scratch'
pseudo_dir = '$PSEUDO_DIR'
outdir = './'
verbosity = 'high'
wf_collect=.true.
/
&system
ibrav = 4,
celldm(1) = 4.703675849
celldm(3) = 2.603711434
nat= 4,
ntyp= 2,
force_symmorphic=.true.
ecutwfc = 100,
nbnd = 120
/
&electrons
diago_david_ndim = 2
diago_full_acc=.true.
diago_thr_init=5.0e-6
mixing_mode = 'plain'
mixing_beta = 0.7
conv_thr = 1.0d-16
/
ATOMIC_SPECIES
B 10.81100 B_LDA_dojo.UPF
N 14.00674 N_LDA_dojo.UPF
ATOMIC_POSITIONS {crystal}
N 0.6666666670 0.3333333330 -0.250000000000
B 0.3333333330 0.6666666670 -0.250000000000
B 0.6666666670 0.3333333330 0.25000000000
N 0.3333333330 0.6666666670 0.25000000000
K_POINTS {automatic}
6 6 2 0 0 0
mpirun -np 4 pw.x -inp hbn.nscf > nscf.out
3. Input hbn.dvscf:
hbn_dvscf &inputph tr2_ph=1.0d-12, verbosity='high' prefix='hBN', fildvscf = 'hBN-dvscf', electron_phonon = 'dvscf', fildyn='hBN.dyn', epsil=.false., ldisp=.true., recover=.true., nq1=6, nq2=6, nq3=2 /
nohup mpirun -np 8 pw.x -inp hbn.dvscf > dvscf.out &
4. Input bse.in (we include 2 valence and 2 conduction bands):
optics # [R] Linear Response optical properties bss # [R] BSE solver bse # [R][BSE] Bethe Salpeter Equation. dipoles # [R] Oscillator strenghts (or dipoles) em1s DIP_CPU= "1 8 1" # [PARALLEL] CPUs for each role DIP_ROLEs= "k c v" # [PARALLEL] CPUs roles (k,c,v) DIP_Threads=0 # [OPENMP/X] Number of threads for dipoles X_and_IO_CPU= "1 1 1 8 1" # [PARALLEL] CPUs for each role X_and_IO_ROLEs= "q g k c v" # [PARALLEL] CPUs roles (q,g,k,c,v) X_and_IO_nCPU_LinAlg_INV=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) X_Threads=0 # [OPENMP/X] Number of threads for response functions BS_CPU= "8 1 1" # [PARALLEL] CPUs for each role BS_ROLEs= "k eh t" # [PARALLEL] CPUs roles (k,eh,t) BS_nCPU_LinAlg_INV=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) BS_nCPU_LinAlg_DIAGO=-1 # [PARALLEL] CPUs for Linear Algebra (if -1 it is automatically set) X_Threads=0 # [OPENMP/X] Number of threads for response functions K_Threads=0 # [OPENMP/BSK] Number of threads for response functions % QpntsRXs 1 | 14 | # [Xs] Transferred momenta % % BndsRnXs 1 | 120 | # [Xs] Polarization function bands % NGsBlkXs= 10 Ry # [Xs] Response block size % LongDrXs 1.000000 | 1.000000 | 1.000000 | # [Xs] [cc] Electric Field % BSEmod= "resonant" # [BSE] resonant/retarded/coupling BSKmod= "SEX" # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc Lkind= "Lfull" # [BSE] Lbar (default) / full BSSmod= "d" # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft` % DipBands 1 | 120 | # [DIP] Bands range for dipoles % DipApproach= "G-space v" # [DIP] [G-space v/R-space x/Covariant/Shifted grids] DipComputed= "R V P" # [DIP] [default R P V; extra P2 Spin Orb] BSENGexx= 30000 Ry # [BSK] Exchange components #ALLGexx # [BSS] Force the use use all RL vectors for the exchange part BSENGBlk= 9000 Ry # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)] % KfnQP_E 1.25997 | 1.08816 | 1.12683 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim % % BSEQptR 1 | 14 | # [BSK] Transferred momenta range % % BSEBands 7 | 10 | # [BSK] Bands range % % BEnRange 0.50000 | 8.00000 | eV # [BSS] Energy range % % BDmRange 0.050000 | 0.050000 | eV # [BSS] Damping range % BEnSteps= 1000 # [BSS] Energy steps % BLongDir 1.000000 | 1.000000 | 0.000000 | # [BSS] [cc] Electric Field % WRbsWF # [BSS] Write to disk excitonic the WFs
nohup mpirun -np 8 yambo -F bse.in -J bse_Lfull -C bse_Lfull &
Importantly, since we want to describe the phonon-assisted recombination process of an *optical* exciton (i.e., emitting a transverse photon), this time we also run an additional calculation at `Q=0` omitting the nonanalytic long-range Coulomb exchange. Make a second input bse_Lbar.in with the following changes:
Lkind= "Lbar" # [BSE] Lbar (default) / full % BSEQptR 1 | 1 | # [BSK] Transferred momenta range %
4b. So now we make a second BSE run in a different directory specified by -J. Here, we also pass to yambo the directory of the previous run as it includes the important screening databases ndb.em1s* that we do not want to recompute from scratch.
mpirun -np 8 yambo -F bse_Lbar.in -J bse_Lbar,bse_Lfull -C bse_Lbar
5. Now we run lelphc (with or without yambopy: in the latter case remember the option -D) to get the el-ph matrix elements, particularly the ndb.elph databases:
yambopy l2y -ph path/of/dvscf/hbn.dvscf -b 7 10 -par 4 2 -D
Luminescence calculation
6. And finally we calculate exciton-phonon matrix elements and the luminescence spectrum in one go using a python script importing the Yambopy exciton-phonon tools: in order to do this, we need to take a look at all the necessary input variables for the formula written above.
We can start from the script luminescence.py available in tutorials/exciton-phonon.
import numpy as np import matplotlib.pyplot as plt from yambopy.exciton_phonon.excph_luminescence import exc_ph_luminescence from yambopy.exciton_phonon.excph_input_data import exc_ph_get_inputs
We import the necessary tools...
path = '3D_hBN' # Path to BSE calculation (Lout--> response is Lfull) bsepath = f'{path}/bse_Lfull' # ndb.BS_diago_Q* databases are needed # Path to BSE calculation for optically active exciton (Lin --> response is Lbar) bseBARpath = f'{path}/bse_Lbar' # ndb.BS_diago_Q1 database is needed # Path to electron-phonon calculation elphpath = path # ndb.elph is needed # Path to unprojected dipoles matrix elements (optional) dipolespath = bsepath # ndb.dipoles is needed (optional) # Path to lattice and k-space info savepath = f'{path}/SAVE' # ns.db1 database is needed
... and we specify the paths to the necessary databases. Note that, if we want to perform polarization averaging, we have to recompute the excitonic dipoles in python as seen here.
What about bseBARpath? This variable points to the directory where the databases for the optical (zero-momentum) excitons [math]\displaystyle{ \alpha }[/math] (which may be computed with Lkind='Lbar') is located, which can be different from the directory with the full indirect exciton dispersion [math]\displaystyle{ \beta }[/math] (usually computed with Lkind='Lfull', however Lkind='Ltilde' can also be used if one is interested in "irreducible" excitons). This makes it possible to compute the coupling between different exciton kinds.
bands_range=[6,10] # 2 valence, 2 conduction bands phonons_range=[0,12] # All phonons nexc_out = 12 # 12 excitonic states at each momentum (Lout) nexc_in = 12 # 12 excitonic states at Q=0 (Lin) T_ph = 10 # Lattice temperature T_exc = 10 # Effective excitonic temperature
emin=4.4 # Energy range and plot details (in eV) emax=4.7 estep=0.0002 broad = 0.005 # Broadening parameter for peak width (in eV)
Next, we specify the parameters for the calculation. We include valence bands from 7 to 10 (6 to 9 in python index) and the contribution of all 12 phonon modes. We consider 12 excitonic states for the coupling matrix elements.
Here T_ph and T_exc are the lattice and excitonic temperatures, respectively.
# We calculate and load all the inputs: # * Exciton-phonon matrix elements # * Excitonic dipole matrix elements # * Exciton energies # * Phonon energies # * We specify bse_path2=bseBARpath meaning we use Lbar calculation for Q=0 excitons input_data = exc_ph_get_inputs(savepath,elphpath,bsepath,\ bse_path2=bseBARpath,dipoles_path=dipolespath,\ nexc_in=12,nexc_out=12,\ bands_range=[6,10],phonons_range=[0,12])
ph_energies, exc_energies, exc_energies_in, G, exc_dipoles = input_data
The function exc_ph_get_inputs gives us all the input data for luminescence in the correct format: phonon energies, exciton energies, optical exciton energies (if needed), exciton-phonon matrix elements (calculated on the fly and printed to file), unprojected exciton dipoles (optional, calculated on the fly and printed to file).
The exc-ph matrix element calculation is just a wrapper of the same tools that we have tested in the above section on MoS2.
Finally, there is the calculation of the luminescence spectrum via the function exc_ph_luminescence:
# We calculate the luminescence spectrum including the input data from before
w,PL = exc_ph_luminescence(T_ph,ph_energies,exc_energies,exc_dipoles,G,\
exc_energies_in=exc_energies_in,exc_temp=T_exc,\
nexc_out=nexc_out,nexc_in=nexc_in,emin=emin,emax=emax,\
estep=estep,broad=broad)
If you want to print the luminescence data for later plotting, you can also add the following line to the script:
# Save to file
data = np.column_stack((w, PL))
np.savetxt("hBN_luminescence_12x12x1.dat", data, fmt="%.8f")
It is now time to run the whole script:
python luminescence.py
NB: By using Yambopy for Step 6, we have limited the use of the Yambo code to just step 4 in the entire workflow. This option is more flexible, as it allows for a greater degree of control by the user. On the other hand the Yambo postprocessing route features a Yambo-style input that doesn't require python knowledge and the calculation is currently faster in fortran. However, the luminescence expression computed in Yambo is a slightly different than this one: it is more approximated in the description of the satellite oscillator strengths, but it explicitly includes the renormalization of the direct exciton peak. You can check the differences here.
Results
We can plot the results of the step 6 calculation. If we do it in the same script we can add something like this:
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlim(emin,emax)
ax.set_ylim(0,np.max(PL)*1.1)
ax.get_yaxis().set_visible(False)
ax.plot(w, PL, '-',c='red', label="AA' hBN luminescence")
plt.legend()
plt.savefig('hBN_luminescence.png')
plt.show()
Here, the signal corresponds to a finite-momentum exciton that recombines with the help of several different phonon modes, both optical and acoustic. Each phonon mode whose coupling with the exciton is allowed can generate a peak, and the energy shifts of these peaks with respect to the initial exciton energy correspond to the phonon energies. This result is underconverged, but the main features are all there. In the plot, we show a more converged example using a 12x12x4 grid (all the other parameters being equal). These plots can be compared with Fig. 4(a) of reference [10].
References
- ↑ Toyozawa, Yutaka, and Chris Oxlade, Optical processes in solids, Cambridge University Press, (2003).
- ↑ G. Antonius, S. G. Louie, Theory of exciton-phonon coupling, Phys. Rev. B, 105, 085111 (2022); arXiv1705.04245 (2017)
- ↑ P. Cudazzo, First-principles description of the exciton-phonon interaction: A cumulant approach, Phys. Rev. B, 102, 045136 (2020); Open access pdf from Luxembourg University
- ↑ F. Paleari, First-principles approaches to the description of indirect absorption and luminescence spectroscopy: exciton-phonon coupling in hexagonal boron nitride, PhD thesis, University of Luxembourg (2019)
- ↑ F. Paleari, and A. Marini, Exciton-phonon interaction calls for a revision of the “exciton” concept, Phys. Rev. B, 106, 125403 (2022); arXiv 2205.02783
- ↑ P. Lechifflart, Exciton-phonon coupling and phonon-assisted luminescence in hexagonal Boron Nitride nanostructures, PhD Thesis, University of Marseille (2023); From the yambo website
- ↑ F. Paleari et al., Exciton-Phonon Coupling in the Ultraviolet Absorption and Emission Spectra of Bulk Hexagonal Boron Nitride, Phys. Rev. Lett. 122, 187401 (2019); arXiv1810.089776
- ↑ E. Cannuccia, B. Monserrat and C. Attaccalite, Theory of phonon-assisted luminescence in solids: Application to hexagonal boron nitride, Phys. Rev. B 99, 081109(R) (2019); arXiv1807.11797
- ↑ Exciton-Phonon Interaction and Relaxation Times from First Principles, Hsiao-Yi Chen, Davide Sangalli, and Marco Bernardi, Phys. Rev. Lett. 125, 107401 (2020); arXiv 2002.08913 (2020)
- ↑ 10.0 10.1 M. Zanfrognini et al., Distinguishing different stackings in layered materials via luminescence spectroscopy, Phys. Rev. Lett. 131, 206902 (2023); arXiv 2305.17554
- ↑ P. Lechifflart, F. Paleari, D. Sangalli, C. Attaccalite, First-principles study of luminescence in hexagonal boron nitride single layer: Exciton-phonon coupling and the role of substrate, Phys. Rev. M, 7 (2), 024006 (2023); arXiv2212.1047
- ↑ 12.0 12.1 Y-h Chan, J. B. Haber, M. H. Naik, J. B. Neaton, D. Y. Qiu, F. H. da Jornada, S. G. Louie, Exciton Lifetime and Optical Line Width Profile via Exciton–Phonon Interactions: Theory and First-Principles Calculations for Monolayer MoS2, Nano Lett., 23, 9 (2023); arXiv 2212.08451 (2023)
- ↑ G. Marini, M. Calandra, P. Cudazzo, Optical absorption and photoluminescence of single layer boron nitride from a first principles cumulant approach, Nano Lett., 24, 20, 6017 (2024); arXiv 2402.03826 (2024)
- ↑ M. Nalabothula, S. Reichardt, L. Wirtz, Origin of Interlayer Exciton–Phonon Coupling in 2D Heterostructures, Nano Lett., 25, 15 (2025), arXiv 2407.16111 (2025)