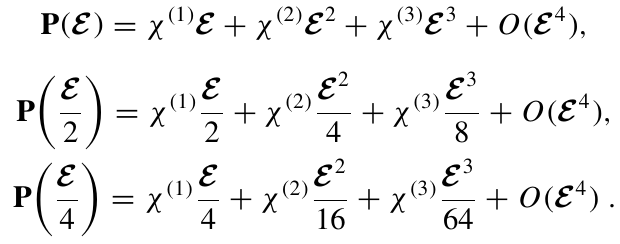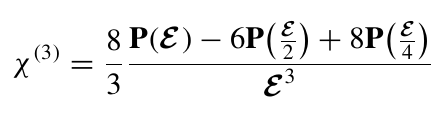Two-photon absorption: Difference between revisions
| (45 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Tpa skeme.png|right|200px | tpa skeme]] | |||
In this tutorial we will show how to calculate two-photon absorption(TPA) in bulk silicon, following the approach descried in Ref. <ref name="tpa">[https://amu.hal.science/hal-01755879/document Two-photon absorption in two-dimensional materials: The case of hexagonal boron nitride] Claudio Attaccalite, Myrta Grüning, Hakim Amara, Sylvain Latil, and François Ducastelle Phys. Rev. B '''98''', 165126 (2018) </ref>. <br>In this tutorial we suppose you are already familiar with the non-linear response using the Yambo code. <br> If it is not the case please study the previous tutorials: [[Linear response using Dynamical Berry Phase]] and [[Real time approach to non-linear response (SHG)]].<br> | In this tutorial we will show how to calculate two-photon absorption(TPA) in bulk silicon, following the approach descried in Ref. <ref name="tpa">[https://amu.hal.science/hal-01755879/document Two-photon absorption in two-dimensional materials: The case of hexagonal boron nitride] Claudio Attaccalite, Myrta Grüning, Hakim Amara, Sylvain Latil, and François Ducastelle Phys. Rev. B '''98''', 165126 (2018) </ref>. <br>In this tutorial we suppose you are already familiar with the non-linear response using the Yambo code. <br> If it is not the case please study the previous tutorials: [[Linear response using Dynamical Berry Phase]] and [[Real time approach to non-linear response (SHG)]].<br> | ||
The tutorial is divided in different steps from the DFT calculation to the final TPA spectrum. For the calculation of the TPA we will use the real-time approach proposed in Ref. <ref name=nl>[https://arxiv.org/abs/1309.4012 Nonlinear optics from an ab initio approach by means of the dynamical Berry phase: Application to second- and third-harmonic generation in semiconductors], C. Attaccalite and M. Grüning, Phys. Rev. B 88, 235113(2013)</ref> | The tutorial is divided in different steps from the DFT calculation to the final TPA spectrum. For the calculation of the TPA we will use the real-time approach proposed in Ref. <ref name=nl>[https://arxiv.org/abs/1309.4012 Nonlinear optics from an ab initio approach by means of the dynamical Berry phase: Application to second- and third-harmonic generation in semiconductors], C. Attaccalite and M. Grüning, Phys. Rev. B '''88''', 235113(2013)</ref><br> | ||
We thank [https://github.com/aim137 Ignacio Martin Alliati] for providing the example and scripts for this tutorial.<br> | |||
== DFT calculations == | == DFT calculations == | ||
| Line 42: | Line 43: | ||
[[File:Extrapolation.png|center|350px| extrapolation]] | [[File:Extrapolation.png|center|350px| extrapolation]] | ||
for more detail see Ref.<ref name=tpa></ref>. Hereafter the three input | for more detail see Ref.<ref name=tpa></ref>. Hereafter the inputs for the real-time simulation. These inputs can be generated using the command <code>yambo_nl -u n -V qp</code>. The first input that we will call<code>input1.in</code> reads: | ||
nloptics # [R] Non-linear spectroscopy | |||
% NLBands | |||
<span style="color:red"> 1 | 7 | </span> # [NL] Bands range | |||
% | |||
NLverbosity= "low" # [NL] Verbosity level (low | high) | |||
NLtime=74.000000 fs # [NL] Simulation Time | |||
NLstep= 0.002500 fs # [NL] Time step length | |||
NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") | |||
NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX") | |||
NLLrcAlpha= 0.000000 # [NL] Long Range Correction | |||
% NLEnRange | |||
<span style="color:red"> 0.200000 | 5.000000 | </span> eV # [NL] Energy range | |||
% | |||
<span style="color:red">NLEnSteps= 24 </span> # [NL] Energy steps | |||
<span style="color:red">NLDamping= 0.100000 </span> eV # [NL] Damping (or dephasing) | |||
#EvalCurrent # [NL] Evaluate the current | |||
% Field1_Dir | |||
<span style="color:red"> 1.000000 | 0.000000 | 0.000000 | </span> # [NL Field1] Field Versor | |||
% | |||
Field1_kind= "SIN" # [NL Field1] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) | |||
% GfnQP_E | |||
<span style="color:red"> 0.600000 | 1.000000 | 1.000000 | </span> # [EXTQP G] E parameters (c/v) eV|adim|adim | |||
% | |||
<span style="color:red">Field1_Int=4.0000E+4 </span> kWLm2 # [NL Field1] Intensity | |||
Field1_Tstart= 0.000000 fs # [NL Field1] Initial Time | |||
the second and third input files (<code>input2.in</code> and <code>input3.in</code>) are equivalent to the first one but with different field intensities: <code>Field1_Int=1.0000E+4</code> and <code>Field1_Int=0.2500E+4</code><br> Notice that the field intensity provided in the input goes as <math>I \propto E^2</math> | |||
Then you can run the three simulations with the command: | |||
yambo_nl -J input1.in -J RUN1 | |||
yambo_nl -J input2.in -J RUN2 | |||
yambo_nl -J input3.in -J RUN3 | |||
Nota bene: these runs are long, they will take approximativelly 3 hours on a serial machine. In order to speed up them you can decrease <code>NLEnSteps=12</code> <br> | |||
or you can run in parallel and add two lines at the beginning of the input: | |||
NL_CPU= "12 1" # [PARALLEL] CPUs for each role | |||
NL_ROLEs= "w k" # [PARALLEL] CPUs roles (w,k) | |||
where 12 is the number of core you want to use. The best is to use a divisor of 24 (number of energy steps). | |||
== Perform Fourier analysis of the polarization == | |||
When real-time simulation are terminated, we can use <code>ypp_nl</code> to analyze the real-time polarization in a way similar to the tutorial on second harmonic generation ([[Real time approach to non-linear response (SHG)]]).<br> | |||
The <code>ypp_fourier.in</code> input, generated with the commanda <code>ypp_nl -u</code>, reads: | |||
nonlinear # [R] Non-linear response analysis | |||
<span style="color:red">Xorder= 5 </span> # Max order of the response/exc functions | |||
% TimeRange | |||
-1.000000 |-1.000000 | fs # Time-window where processing is done | |||
# From here onwards, it is ignored in SHG | |||
% | |||
ETStpsRt= 200 # Total Energy steps | |||
% EnRngeRt | |||
0.00000 | 10.00000 | eV # Energy range | |||
% | |||
DampMode= "NONE" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) | |||
DampFactor= 0.000000 eV # Damping parameter | |||
you can do: | |||
ypp_nl -F ypp_fourier.in -J RUN1 | |||
ypp_nl -F ypp_fourier.in -J RUN2 | |||
ypp_nl -F ypp_fourier.in -J RUN3 | |||
this will produce the corresponding coefficients χ<sup>1</sup>(ω)=P(ω)/E(ω), χ<sup>2</sup>(2ω)=P(2ω)/E<sup>2</sup>(ω), χ<sup>3</sup>, etc.. in the file <code>o-RUN1.YPP-order </code>... | |||
== Use Richardson extrapolation to extract the TPA == | == Use Richardson extrapolation to extract the TPA == | ||
Finally we will use the formula: | |||
[[File:Extrapolation.png|center|350px| extrapolation]] | |||
to combine the different polarization and extract the TPA coefficient. This can be done using the following script: | |||
[https://www.attaccalite.com/tutorials_yambo/NLAbsorption_PP.py NLAbsorption_PP.py] <br> | |||
Do not forget to set the correct file name and path in the the python script, then you can execute it with the command: | |||
python3 NLAbsorption_PP.py -nr 3 | |||
The result can be plotted using gnuplot with the script: [https://www.attaccalite.com/tutorials_yambo/plot-ip-tpa.gpi plot-ip-tpa.gpi] | |||
[[File:Fig-TPA-IPA-Si 24.png|center|600px|TPA_silicon_24]] | |||
This result was calculated with few energy steps (NLEnSteps= 24) but if you increase this number you can get a smoother result, but this will require more computational time. | |||
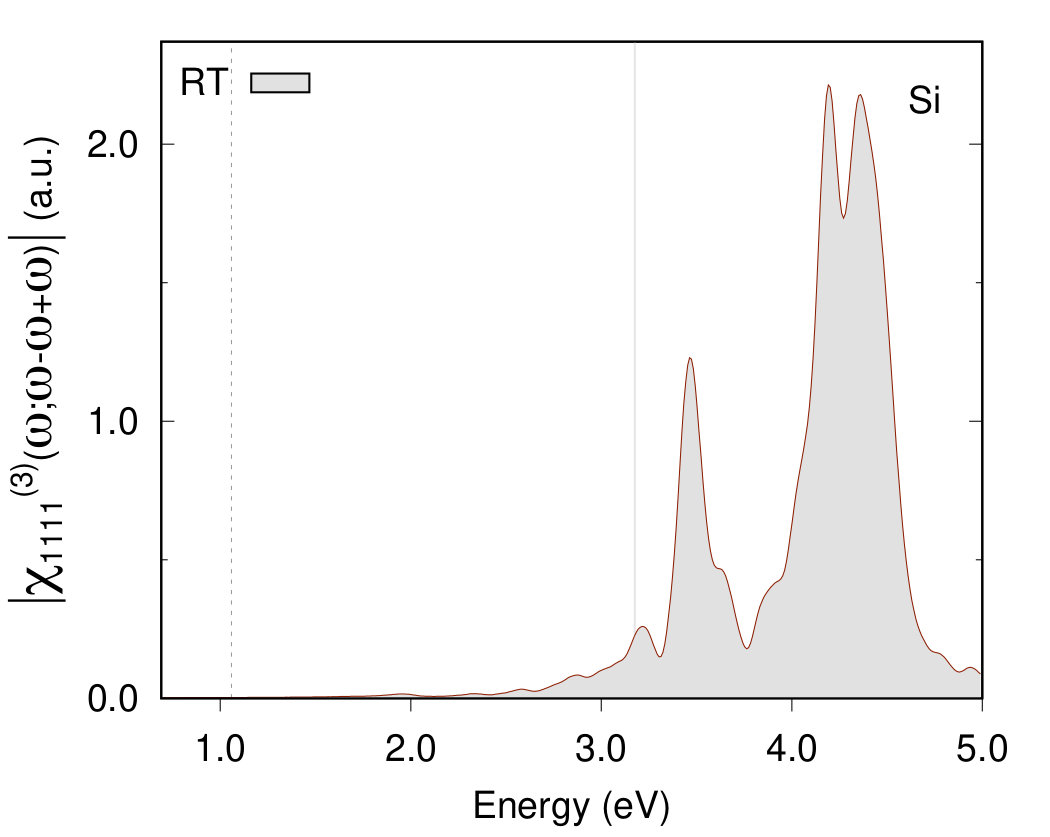
For example in the figure below we used 481 energy steps. | |||
[[File:Fig-TPA-IPA-Si.png|center| 600px | tpa converged]] | |||
== References == | == References == | ||
Latest revision as of 09:33, 11 December 2024
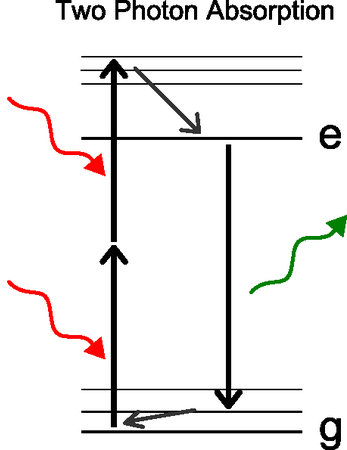
In this tutorial we will show how to calculate two-photon absorption(TPA) in bulk silicon, following the approach descried in Ref. [1].
In this tutorial we suppose you are already familiar with the non-linear response using the Yambo code.
If it is not the case please study the previous tutorials: Linear response using Dynamical Berry Phase and Real time approach to non-linear response (SHG).
The tutorial is divided in different steps from the DFT calculation to the final TPA spectrum. For the calculation of the TPA we will use the real-time approach proposed in Ref. [2]
We thank Ignacio Martin Alliati for providing the example and scripts for this tutorial.
DFT calculations
Here we provide input files for QuantumEspresso both the self-consistent calculation and the non-self-consistent: QE_silicon.tgz
Run them, import the wave-function in Yambo and run the setup. (see previous tutorials).
Removing symmetries
In this tutorial we will calculate the TPA along the 'x' direction therefore we remove symmetries not compatible with an external field along this direction, with the command ypp_nl -y:
fixsyms # [R] Remove symmetries not consistent with an external perturbation % Efield1 1.000000 | 0.000000 | 0.000000 | # First external Electric Field % % Efield2 0.000000 | 0.000000 | 0.000000 | # Additional external Electric Field % BField= 0.000000 T # [MAG] Magnetic field modulus Bpsi= 0.000000 deg # [MAG] Magnetic field psi angle [degree] Btheta= 0.000000 deg # [MAG] Magnetic field theta angle [degree] #RmAllSymm # Remove all symmetries RmTimeRev # Remove Time Reversal #RmSpaceInv # Remove Spatial Inversion
the you can go in the FixSymm folder and run the setup again.
Calculations at different field intensities
In order to extract the TPA coefficient we will run a series of simulation at different intensities of the external field: Ε, Ε/2, Ε/4. The polarization obtained from these simulation can be expanded in the field as:
then we will combine them to obtain the TPA coefficient as:
for more detail see Ref.[1]. Hereafter the inputs for the real-time simulation. These inputs can be generated using the command yambo_nl -u n -V qp. The first input that we will callinput1.in reads:
nloptics # [R] Non-linear spectroscopy % NLBands 1 | 7 | # [NL] Bands range % NLverbosity= "low" # [NL] Verbosity level (low | high) NLtime=74.000000 fs # [NL] Simulation Time NLstep= 0.002500 fs # [NL] Time step length NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.200000 | 5.000000 | eV # [NL] Energy range % NLEnSteps= 24 # [NL] Energy steps NLDamping= 0.100000 eV # [NL] Damping (or dephasing) #EvalCurrent # [NL] Evaluate the current % Field1_Dir 1.000000 | 0.000000 | 0.000000 | # [NL Field1] Field Versor % Field1_kind= "SIN" # [NL Field1] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN) % GfnQP_E 0.600000 | 1.000000 | 1.000000 | # [EXTQP G] E parameters (c/v) eV|adim|adim % Field1_Int=4.0000E+4 kWLm2 # [NL Field1] Intensity Field1_Tstart= 0.000000 fs # [NL Field1] Initial Time
the second and third input files (input2.in and input3.in) are equivalent to the first one but with different field intensities: Field1_Int=1.0000E+4 and Field1_Int=0.2500E+4
Notice that the field intensity provided in the input goes as [math]\displaystyle{ I \propto E^2 }[/math]
Then you can run the three simulations with the command:
yambo_nl -J input1.in -J RUN1 yambo_nl -J input2.in -J RUN2 yambo_nl -J input3.in -J RUN3
Nota bene: these runs are long, they will take approximativelly 3 hours on a serial machine. In order to speed up them you can decrease NLEnSteps=12
or you can run in parallel and add two lines at the beginning of the input:
NL_CPU= "12 1" # [PARALLEL] CPUs for each role NL_ROLEs= "w k" # [PARALLEL] CPUs roles (w,k)
where 12 is the number of core you want to use. The best is to use a divisor of 24 (number of energy steps).
Perform Fourier analysis of the polarization
When real-time simulation are terminated, we can use ypp_nl to analyze the real-time polarization in a way similar to the tutorial on second harmonic generation (Real time approach to non-linear response (SHG)).
The ypp_fourier.in input, generated with the commanda ypp_nl -u, reads:
nonlinear # [R] Non-linear response analysis
Xorder= 5 # Max order of the response/exc functions
% TimeRange
-1.000000 |-1.000000 | fs # Time-window where processing is done
# From here onwards, it is ignored in SHG
%
ETStpsRt= 200 # Total Energy steps
% EnRngeRt
0.00000 | 10.00000 | eV # Energy range
%
DampMode= "NONE" # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor= 0.000000 eV # Damping parameter
you can do:
ypp_nl -F ypp_fourier.in -J RUN1 ypp_nl -F ypp_fourier.in -J RUN2 ypp_nl -F ypp_fourier.in -J RUN3
this will produce the corresponding coefficients χ1(ω)=P(ω)/E(ω), χ2(2ω)=P(2ω)/E2(ω), χ3, etc.. in the file o-RUN1.YPP-order ...
Use Richardson extrapolation to extract the TPA
Finally we will use the formula:
to combine the different polarization and extract the TPA coefficient. This can be done using the following script:
NLAbsorption_PP.py
Do not forget to set the correct file name and path in the the python script, then you can execute it with the command:
python3 NLAbsorption_PP.py -nr 3
The result can be plotted using gnuplot with the script: plot-ip-tpa.gpi
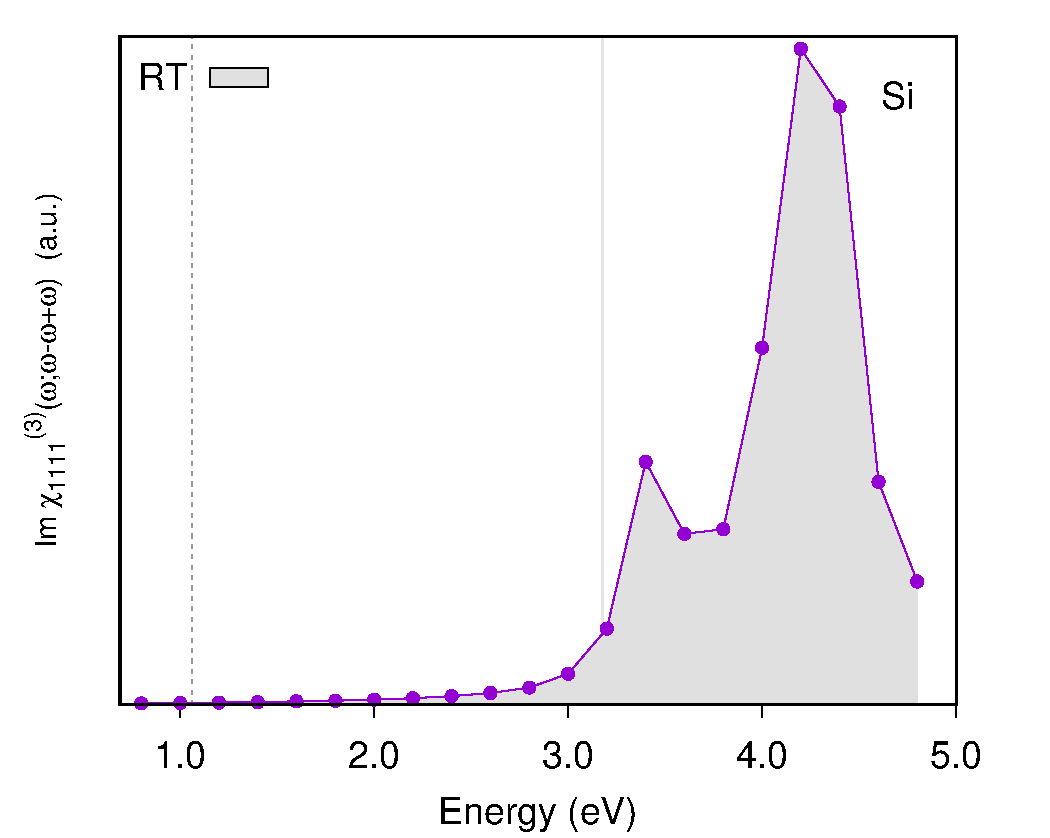
This result was calculated with few energy steps (NLEnSteps= 24) but if you increase this number you can get a smoother result, but this will require more computational time. For example in the figure below we used 481 energy steps.
References
- ↑ 1.0 1.1 Two-photon absorption in two-dimensional materials: The case of hexagonal boron nitride Claudio Attaccalite, Myrta Grüning, Hakim Amara, Sylvain Latil, and François Ducastelle Phys. Rev. B 98, 165126 (2018)
- ↑ Nonlinear optics from an ab initio approach by means of the dynamical Berry phase: Application to second- and third-harmonic generation in semiconductors, C. Attaccalite and M. Grüning, Phys. Rev. B 88, 235113(2013)