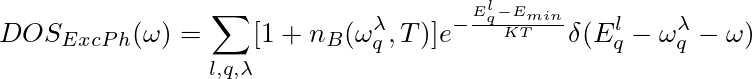Optical properties at finite temperature: Difference between revisions

From The Yambo Project
Jump to navigation Jump to search
No edit summary
 
(27 intermediate revisions by 4 users not shown)
Line 5: Line 5:
The tutorial is dived into different steps first we will calculate absorption at independent particle approximation, <br>then we will include excitonic effects,
The tutorial is dived into different steps first we will calculate absorption at independent particle approximation, <br>then we will include excitonic effects,
and finally, we will show how to analyze the data.<br>
and finally, we will show how to analyze the data.<br>
''' <span style="color:red">WARNING</span>''': Calculations in this tutorial are performed without double-grid, please check if the file <code>SAVE/ndb.PH_DoubleGrid</code>  is present in your calculations, then remove it and rerun electron-phonon coupling before proceed with optics.


'''Notice that there are two ways to include finite temperature effects in the BSE''':
'''Notice that there are two ways to include finite temperature effects in the BSE''':
* The first is to use a full Bethe-Salpeter equation with all the coupling terms in such a way to treat complex quasi-particles that cannot be handled in standard (Hermitian) BSE, this is explained in section [[https://www.yambo-code.org/wiki/index.php?title=Optical_properties_at_finite_temperature#Bethe-Salpeter_at_finite_temperature_.28diagonalization_solver.29 Bethe-Salpeter at finite temperature (diagonalization solver)]]. This approach has the advantage that one can obtain excitonic eigenvalues and eigenfunctions at finite temperature and not only the optical spectrum.
* The first is to use a full Bethe-Salpeter equation with all the coupling terms in such a way to treat complex quasi-particles that cannot be handled in standard (Hermitian) BSE, this is explained in section [[https://www.yambo-code.org/wiki/index.php?title=Optical_properties_at_finite_temperature#Bethe-Salpeter_at_finite_temperature_.28diagonalization_solver.29 Bethe-Salpeter at finite temperature (diagonalization solver)]]. This approach has the advantage that one can obtain excitonic eigenvalues and eigenfunctions at finite temperature and not only the optical spectrum.
   
   
* The second method is use of a standard Hermitina (resonant) BSE plus the inversion solver <ref name='dbgrid'>D. Kammerlander et al. [Phys. Rev. B 86, 125203, https://arxiv.org/abs/1209.1509] </ref>. In this case, a Lo two-particle Green's function that contains the complex quasi-particles is used in the solver to get a finite temperature spectrum. This approach has the advantage that can be used with the double-grid but it does not give access to eigenvalues and eigenfunctions of the BSE. This approach is described in the section: [[https://www.yambo-code.org/wiki/index.php?title=Optical_properties_at_finite_temperature#Bethe-Salpeter_at_finite_temperature_.28inversion_solver.29 Bethe-Salpeter at finite temperature (inversion solver)]]
* The second method is use of a standard Hermitinan (resonant) BSE plus the inversion solver <ref name='dbgrid'>D. Kammerlander et al. [https://arxiv.org/abs/1209.1509 Phys. Rev. B '''86''', 125203] </ref>. In this case, a Lo two-particle Green's function that contains the complex quasi-particles is used in the solver to get a finite temperature spectrum. This approach has the advantage that can be used with the double-grid but it does not give access to eigenvalues and eigenfunctions of the BSE. This approach is described in the section: [[https://www.yambo-code.org/wiki/index.php?title=Optical_properties_at_finite_temperature#Bethe-Salpeter_at_finite_temperature_.28inversion_solver.29 Bethe-Salpeter at finite temperature (inversion solver)]]




Line 22: Line 24:
  ....
  ....
and save the results of the 0K and 300K temperature in two separate folder with the -J option.  
and save the results of the 0K and 300K temperature in two separate folder with the -J option.  
Now you can use the correction to the energy levels and the induced width to calculate the optical absorption at finite temperature. Generate the input with the command  ''yambo_ph -o c -V qp''
Now you can use the correction to the energy levels and the induced width to calculate the optical absorption at finite temperature. Generate the input with the command  <code>yambo_ph -o c -V qp -F yambo.in_300K</code>:


  optics                          # [R] Linear Response optical properties
  optics                          # [R] Linear Response optical properties
Line 29: Line 31:
  Chimod= "IP"                    # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  Chimod= "IP"                    # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  % QpntsRXd
  % QpntsRXd
  1 | 1 |                             # [Xd] Transferred momenta
<span style="color:red"> 1 | 1 |   </span>                          # [Xd] Transferred momenta
  %
  %
  % BndsRnXd
  % BndsRnXd
  2 |  7 |                           # [Xd] Polarization function bands
  <span style="color:red"> 2 |  7 | </span>                        # [Xd] Polarization function bands
  %
  %
  % EnRngeXd
  % EnRngeXd
  0.000000 | 5.000000 |         eV    # [Xd] Energy range
<span style="color:red"> 0.000000 | 5.000000 | </span>        eV    # [Xd] Energy range
  %
  %
  % DmRngeXd
  % DmRngeXd
   0.0100000 | 0.0100000 |         eV    # [Xd] Damping range
   <span style="color:red">0.0100000 | 0.0100000 | </span>        eV    # [Xd] Damping range
  %
  %
  ETStpsXd=  1500                   # [Xd] Total Energy steps
  <span style="color:red">ETStpsXd=  1500 </span>                  # [Xd] Total Energy steps
  % LongDrXd
  % LongDrXd
   1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
   1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
Line 46: Line 48:
  <span style="color:red">XfnQPdb= "E W < T300/ndb.QP" </span>    # [EXTQP Xd] Database action
  <span style="color:red">XfnQPdb= "E W < T300/ndb.QP" </span>    # [EXTQP Xd] Database action


set the path of the ''ndb.QP'' you want to read and perform the calculations. Notice that from the QP database we read two quantities the correction to the energy levels  <span style="color:blue">E</span> and the width  <span style="color:blue">W</span>. In this calculation we also included a small smearing 0.01eV to mimic the electronic smearing. Hereafter the result without and with electron-phonon coupling at two different temperatures:
set the path of the ''ndb.QP'' you want to read and perform the calculations. Notice that from the QP database we read two quantities the correction to the energy levels  <span style="color:blue">E</span> and the width  <span style="color:blue">W</span>. In this calculation we also included a small smearing 0.01eV to mimic the electronic smearing. Run your calculations with the command: <code>yambo_ph -F yambo.in_300K -J T300</code> and do the same for the 0K case.<br>
<br>You can plot the results with gnuplot using the command: <code> plot 'o-T300.eps_q1_ip' w l t '300 K', 'o-T0.eps_q1_ip' w l t '0 K'</code>.<br> Hereafter the result without and with electron-phonon coupling at two different temperatures:
[[File:Si absorption finite t.png|800px|center |Absorption of bulk silicon at finite temperature]]
[[File:Si absorption finite t.png|800px|center |Absorption of bulk silicon at finite temperature]]


Line 55: Line 58:
In this section we will calculate the Bethe-Salpeter at finite temperature using the full-BSE.
In this section we will calculate the Bethe-Salpeter at finite temperature using the full-BSE.


You can generate the input using the command <code>yambo_ph -X s -o b -k sex -y d -V qp</code>
You can generate the input using the command <code>yambo_ph -X s -o b -k sex -y d -V qp -F yambo.in_BSE</code>


  em1s                            # [R][Xs] Statically Screened Interaction
  em1s                            # [R][Xs] Statically Screened Interaction
Line 66: Line 69:
  K_Threads=0                      # [OPENMP/BSK] Number of threads for response functions
  K_Threads=0                      # [OPENMP/BSK] Number of threads for response functions
  Chimod= "HARTREE"                # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  Chimod= "HARTREE"                # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  BSEmod= "coupling"               # [BSE] resonant/retarded/coupling
  <span style="color:red">BSEmod= "coupling"     </span>        # [BSE] resonant/retarded/coupling
  BSKmod= "SEX"                    # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
  BSKmod= "SEX"                    # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
  BSSmod= "d"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
  BSSmod= "d"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
Line 82: Line 85:
  %
  %
  % BSEBands
  % BSEBands
  2 |  7 |                          # [BSK] Bands range
  <span style="color:red"> 2 |  7 |</span>                           # [BSK] Bands range
  %
  %
  % BEnRange
  % BEnRange
   0.000000 | 5.000000 |        eV    # [BSS] Energy range
   <span style="color:red">0.000000 | 5.000000 |</span>         eV    # [BSS] Energy range
  %
  %
  % BDmRange
  % BDmRange
  0.010000 | 0.010000 |         eV    # [BSS] Damping range
  <span style="color:red">0.010000 | 0.010000 | </span>        eV    # [BSS] Damping range
  %
  %
  <span style="color:red">BEnSteps= 1500    </span>              # [BSS] Energy steps
  <span style="color:red">BEnSteps= 1500    </span>              # [BSS] Energy steps
Line 95: Line 98:
  %
  %
  #WRbsWF                        # [BSS] Write to disk excitonic the WFs
  #WRbsWF                        # [BSS] Write to disk excitonic the WFs
XfnQPdb= "none"                  # [EXTQP Xd] Database action
XfnQP_INTERP_NN= 1              # [EXTQP Xd] Interpolation neighbours (NN mode)
XfnQP_INTERP_shells= 20.00000    # [EXTQP Xd] Interpolation shells (BOLTZ mode)
XfnQP_DbGd_INTERP_mode= "NN"    # [EXTQP Xd] Interpolation DbGd mode
% XfnQP_E
  0.000000 | 1.000000 | 1.000000 |        # [EXTQP Xd] E parameters  (c/v) eV|adim|adim
%
XfnQP_Z= ( 1.000000 , 0.000000 )        # [EXTQP Xd] Z factor  (c/v)
XfnQP_Wv_E= 0.000000      eV    # [EXTQP Xd] W Energy reference  (valence)
% XfnQP_Wv
  0.000000 | 0.000000 | 0.000000 |        # [EXTQP Xd] W parameters  (valence) eV| 1|eV^-1
%
XfnQP_Wv_dos= 0.000000    eV    # [EXTQP Xd] W dos pre-factor  (valence)
XfnQP_Wc_E= 0.000000      eV    # [EXTQP Xd] W Energy reference  (conduction)
% XfnQP_Wc
  0.000000 | 0.000000 | 0.000000 |        # [EXTQP Xd] W parameters  (conduction) eV| 1 |eV^-1
%
XfnQP_Wc_dos= 0.000000    eV    # [EXTQP Xd] W dos pre-factor  (conduction)
  % BndsRnXs
  % BndsRnXs
   1 | 12 |                          # [Xs] Polarization function bands
   1 | 12 |                          # [Xs] Polarization function bands
  %
  %
  NGsBlkXs= 113                RL   # [Xs] Response block size
  <span style="color:red">NGsBlkXs= 113                RL </span>  # [Xs] Response block size
  % LongDrXs
  % LongDrXs
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
Line 123: Line 108:




In this input file we asked Yambo to include finite temperature quasi-particle in the BSE with the line <code>KfnQPdb= "E W < T0/ndb.QP" </code>, notice that we also introduce an additional rigid shift of 0.5 eV to mimic the GW correction with the line <code> 0.500000 | 1.000000 | 1.000000 |  \# [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim</code>. In principle you can calculate the GW correction following the [https://www.yambo-code.org/wiki/index.php?title=How_to_obtain_the_quasi-particle_band_structure_of_a_bulk_material:_h-BN this tutorial] and then merge the corresponding ndb.QP database with the one of the electron-phonon coupling using the command <code> ypp -qpdb m</code>.
In this input file we asked Yambo to include finite temperature quasi-particle in the BSE with the line <code>KfnQPdb= "E W < T0/ndb.QP" </code>, notice that we also introduce an additional rigid shift of 0.5 eV to mimic the GW correction with the line <code> 0.500000 | 1.000000 | 1.000000 |  \# [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim</code>. You can now run the calculation with the command <code> yambo_ph -F yambo.in_BSE -J T0_BSE</code><br>
In principle you can calculate the GW correction following the [https://www.yambo-code.org/wiki/index.php?title=How_to_obtain_the_quasi-particle_band_structure_of_a_bulk_material:_h-BN this tutorial] and then merge the corresponding ndb.QP database with the one of the electron-phonon coupling using the command <code> ypp -qpdb m</code>.
Notice that we changed the BSE type to "coupling" because you need the full Bethe-Salpeter to deal with complex quasi-particles.<br>
Notice that we changed the BSE type to "coupling" because you need the full Bethe-Salpeter to deal with complex quasi-particles.<br>
 
Now we do the same calculation at T = 300 K. Copy the previous input file <code> cp yambo.in_BSE yambo.in_BSE_300</code>. Then modify where the code reads the QP database :
<span style="color:red">KfnQPdb= "E W < T300/ndb.QP"  </span>    # [EXTQP BSK BSS] Database action
Run the command with <code>yambo_ph -F yambo.in_BSE_300 -J T300_BSE</code><br>
Finally, you should be able to plot the absorption spectra from the outputs in gnuplot :
<code> plot 'o-T0_BSE.eps_q1_diago_bse' w l t '0 K', 'o-T300_BSE.eps_q1_diago_bse' w l t '300 K'</code>
[[File:Si bse optics.png|800px|center |Bethe-Salpeter at finite temperature for bulk silicom]]
[[File:Si bse optics.png|800px|center |Bethe-Salpeter at finite temperature for bulk silicom]]


Line 131: Line 121:
In this calculation we have made different approximations:<br>
In this calculation we have made different approximations:<br>
1) we did not include the renormalization of excitons due to the change of the screening potential W with temperature. Including electron-phonon coupling
1) we did not include the renormalization of excitons due to the change of the screening potential W with temperature. Including electron-phonon coupling
in the dielectric constant by changing the line <code> XfnQPdb= "none" </code> is unfortunately not enough, for a discussion see ref. <ref>L. Adamska and P. Umari, [https://journals.aps.org/prb/abstract/10.1103/PhysRevB.103.075201 Phys. Rev. B 103, 075201 (2021)] </ref><br>
in the dielectric constant by changing the line <code> XfnQPdb= "none" </code> is unfortunately not enough, for a discussion see ref. <ref>L. Adamska and P. Umari, [https://journals.aps.org/prb/abstract/10.1103/PhysRevB.103.075201 Phys. Rev. B '''103''', 075201 (2021)] </ref><br>
2) The electron-phonon coupling should enter in the BSE through the exciton-phonon matrix elements and not from the single-particle self-energy, as we have done in this tutorial. The approximation used in this tutorial is valid for not too strong bound excitons, and in general it generated a finite life-time also for the lowest exciton in direct materials that is not correct. For a discussion see refs. <ref name='claudio'> see Supp. Mat. of [https://journals.aps.org/prb/abstract/10.1103/PhysRevB.99.081109 Phys. Rev. B '''99''', 081109(R) (2019)]</ref><ref name='fulvio'>F. Paleari, [https://orbilu.uni.lu/handle/10993/41058 Phd Thesis (2019)]</ref> and <ref>H. Chen, D. Sangalli, and M. Bernardi [https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.107401 Phys. Rev. Lett. 125, 107401 (2020)]</ref>.<br>
2) The electron-phonon coupling should enter in the BSE through the exciton-phonon matrix elements and not from the single-particle self-energy, as we have done in this tutorial. The approximation used in this tutorial is valid for not too strong bound excitons, and in general it generated a finite life-time also for the lowest exciton in direct materials that is not correct. For a discussion see refs.<ref>G. Antonius, S. G. Louie [https://arxiv.org/abs/1705.04245 Phys. Rev. B '''105''', 085111 (2022)]</ref><ref name='claudio'> see Supp. Mat. of [https://journals.aps.org/prb/abstract/10.1103/PhysRevB.99.081109 Phys. Rev. B '''99''', 081109(R) (2019)]</ref><ref name='fulvio'>F. Paleari, [https://orbilu.uni.lu/handle/10993/41058 Phd Thesis (2019)]</ref> and <ref>H. Chen, D. Sangalli, and M. Bernardi [https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.107401 Phys. Rev. Lett. '''125''', 107401 (2020)]</ref>.<br>
3) we did not include scattering between exciton and phonons, therefore our results do not contain phonon-assisted absorption peaks, you can include these terms by finite difference displacements see refs. <ref name='fulvio'></ref>.
3) we did not include scattering between exciton and phonons, therefore our results do not contain phonon-assisted absorption peaks, you can include these terms by finite difference displacements see refs. <ref name='fulvio'></ref>.


== Result analysis ==
== Result analysis ==
Results of BSE at finite temperature can be analized in the same way of standard BSE. You can plot exciton binging energy as a function of the temperature, exciton wave-function and so, see [https://www.yambo-code.org/wiki/index.php?title=How_to_analyse_excitons Exciton Plot tutorial].
Results of BSE at finite temperature can be analized in the same way of standard BSE. You can plot exciton binging energy as a function of the temperature, exciton wave-function and so, see [https://www.yambo-code.org/wiki/index.php?title=How_to_analyse_excitons Exciton Plot tutorial].
For example if you sort exciton with the command <code> ypp_ph -e s</code> for the case T=0K, in addition to the exciton energy now you will find its line-width in the files .
For example if you sort exciton with the command <code> ypp_ph -e s -J T0_BSE</code> for the case T=0K, in addition to the exciton energy now you will find its line-width in the files .
<code>o.exc_qpt1_E_sorted</code> and <code>o.exc_qpt1_I_sorted</code>.
<code>o-T0_BSE.exc_qpt1_E_sorted</code> and <code>o-T0_BSE.exc_qpt1_I_sorted</code>.
  #
  #
  #    Maximum Residual Value = .72765E+05
  #    Maximum Residual Value = .77136E+05
  #   
  #   
  #    E [ev]            Strength          Index              W [meV]
  #    E [ev]            Strength          Index              W [meV]
  #
  #
  ...............
  ...............
3.13603616       0.894595146        274.000000        38.3100700
    2.82974172       0.388171151E-1      335.000000        11.9707289
3.13607597       0.458951890         276.000000        38.3091507
    2.82976580       0.110338017         334.000000        11.9676380
3.13608289       0.936879739E-1      278.000000        38.3060684
    2.82979798       0.992550552        333.000000        11.9646358
3.13852167       0.135797265E-3     279.000000        36.6859016
    2.83366466       0.177820283E-2     336.000000        6.12744808
3.13854289       0.166505214E-2     277.000000        36.6878891
    2.83368802       0.183327938E-3     338.000000        6.12689734
3.13856506       0.185914442E-2     275.000000        36.6866493
    2.83369708       0.679280609E-3     337.000000        6.12836981
3.18071890       0.344193308E-3      328.000000        35.5702744
    2.87943292       0.146849517E-3      332.000000        2.51892495
3.18077826       0.227900382E-4     329.000000        35.5690689
    2.87945318       0.295515812E-3     331.000000        2.51745558
3.19683385       0.355413969E-3      327.000000        34.4151421
    2.89804840       0.539837289E-3      330.000000        1.42265606
3.23861122       0.210206732         330.000000        42.7790527
    2.93557525       0.532299697         329.000000        12.5491867
3.23862171       0.387398720         332.000000        42.7778893
    2.93559408       0.214365616         391.000000        12.5504198
3.23863339       0.522650003         331.000000        42.7766075
    2.93561029       0.175688639         390.000000        12.5498590
 
    2.97320676        0.158064649E-3      388.000000        9.35168839
Notice that in the files you will find many exciton with negative energy due the full-BSE nature, finally consider line-width numbers with care due to the approximation described above.
    2.97321057        0.300355150E-4      408.000000        9.35530090
 
    2.97321224        0.931323011E-4      389.000000        9.35327435
    2.97682190        0.551215744E-4      405.000000        8.87609196


'''Notice''' that in the files you will find many excitons with negative energy due the anti-resonant part of the full-BSE.


== Excitonic Eliashberg Functions ==
== Excitonic Eliashberg Functions ==
If you run the BSE and save the excitonic wave-functions (uncomment the flag <code>WRbsWF</code> in the BSE input file), tt is possible to plot the excitonic Eliashberg Functions with the command <code> ypp_ph -e e</code>.
If you run the BSE and save the excitonic wave-functions (uncomment the flag <code>WRbsWF</code> in the BSE input file), tt is possible to plot the excitonic Eliashberg Functions with the command <code> ypp_ph -e e</code>.
For an interpretation of these functions see the discussion in reference <ref>Andrea Marini
For an interpretation of these functions see the discussion in reference <ref>Andrea Marini
  [https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.106405 Phys. Rev. Lett. 101, 106405 (2008)]</ref>
  [https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.106405 Phys. Rev. Lett. '''101''', 106405 (2008)]</ref>


== Bethe-Salpeter at finite temperature (inversion solver) ==
== Bethe-Salpeter at finite temperature (inversion solver) ==


It is possible to take into account complex quasi-particles in the BSE solution by means of the inversion procedure.
It is possible to take into account complex quasi-particles in the BSE solution by means of the inversion procedure.
The idea is to construct an Lo (Eq. 5 of Ref.<ref name='dbgrid'></re>) that includes the electron-phonon corrections including the imaginary part.
The idea is to construct an Lo (Eq. 5 of Ref.<ref name='dbgrid'></ref>) that includes the electron-phonon corrections including the imaginary part.
In order to generate the input you can type: <code>yambo_ph -X s -o b -k sex -y i -V qp</code>
In order to generate the input you can type: <code>yambo_ph -X s -o b -k sex -y i -V qp</code>


Line 208: Line 200:
  <span style="color:red">  0.010000 | 0.010000 |  </span>      eV    # [BSS] Damping range
  <span style="color:red">  0.010000 | 0.010000 |  </span>      eV    # [BSS] Damping range
  %
  %
  <span style="color:red">BEnSteps= 500 </span>                  # [BSS] Energy steps
  <span style="color:red">BEnSteps= 1500 </span>                  # [BSS] Energy steps
  % BLongDir  
  % BLongDir  
   1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
   1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
Line 217: Line 209:
   1 | 12 |                          # [Xs] Polarization function bands
   1 | 12 |                          # [Xs] Polarization function bands
  %
  %
  NGsBlkXs= 113             RL    # [Xs] Response block size
  <span style="color:red">NGsBlkXs= 113 </span>            RL    # [Xs] Response block size
  % LongDrXs
  % LongDrXs
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field

Latest revision as of 19:54, 24 May 2022

Yambo tutorial image

In this tutorial, we will show you how to calculate optical properties including thermal effects due to the electron-phonon coupling.
This tutorial assumes that you have completed all the steps from the previous tutorial on Electron Phonon Coupling.
The tutorial is dived into different steps first we will calculate absorption at independent particle approximation,
then we will include excitonic effects, and finally, we will show how to analyze the data.

WARNING: Calculations in this tutorial are performed without double-grid, please check if the file SAVE/ndb.PH_DoubleGrid is present in your calculations, then remove it and rerun electron-phonon coupling before proceed with optics.

Notice that there are two ways to include finite temperature effects in the BSE:

  • The first is to use a full Bethe-Salpeter equation with all the coupling terms in such a way to treat complex quasi-particles that cannot be handled in standard (Hermitian) BSE, this is explained in section [Bethe-Salpeter at finite temperature (diagonalization solver)]. This approach has the advantage that one can obtain excitonic eigenvalues and eigenfunctions at finite temperature and not only the optical spectrum.
  • The second method is use of a standard Hermitinan (resonant) BSE plus the inversion solver [1]. In this case, a Lo two-particle Green's function that contains the complex quasi-particles is used in the solver to get a finite temperature spectrum. This approach has the advantage that can be used with the double-grid but it does not give access to eigenvalues and eigenfunctions of the BSE. This approach is described in the section: [Bethe-Salpeter at finite temperature (inversion solver)]


Absorption at finite temperature

Now you repeat the previous calculation but including all k-points, the last 3 valence and the first 3 conduction bands: 

.....
%QPkrange                        # [GW] QP generalized Kpoint/Band indices
1|8|2|7|
%
....

and save the results of the 0K and 300K temperature in two separate folder with the -J option. Now you can use the correction to the energy levels and the induced width to calculate the optical absorption at finite temperature. Generate the input with the command yambo_ph -o c -V qp -F yambo.in_300K: 

optics                           # [R] Linear Response optical properties
chi                              # [R][CHI] Dyson equation for Chi.
dipoles                          # [R] Oscillator strenghts (or dipoles)
Chimod= "IP"                     # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% QpntsRXd
 1 | 1 |                             # [Xd] Transferred momenta
%
% BndsRnXd
  2 |  7 |                           # [Xd] Polarization function bands
%
% EnRngeXd
 0.000000 | 5.000000 |         eV    # [Xd] Energy range
%
% DmRngeXd
 0.0100000 | 0.0100000 |         eV    # [Xd] Damping range
%
ETStpsXd=  1500                    # [Xd] Total Energy steps
% LongDrXd
 1.000000 | 0.000000 | 0.000000 |        # [Xd] [cc] Electric Field
%
XfnQPdb= "E W < T300/ndb.QP"      # [EXTQP Xd] Database action

set the path of the ndb.QP you want to read and perform the calculations. Notice that from the QP database we read two quantities the correction to the energy levels E and the width W. In this calculation we also included a small smearing 0.01eV to mimic the electronic smearing. Run your calculations with the command: yambo_ph -F yambo.in_300K -J T300 and do the same for the 0K case.

You can plot the results with gnuplot using the command: plot 'o-T300.eps_q1_ip' w l t '300 K', 'o-T0.eps_q1_ip' w l t '0 K'.
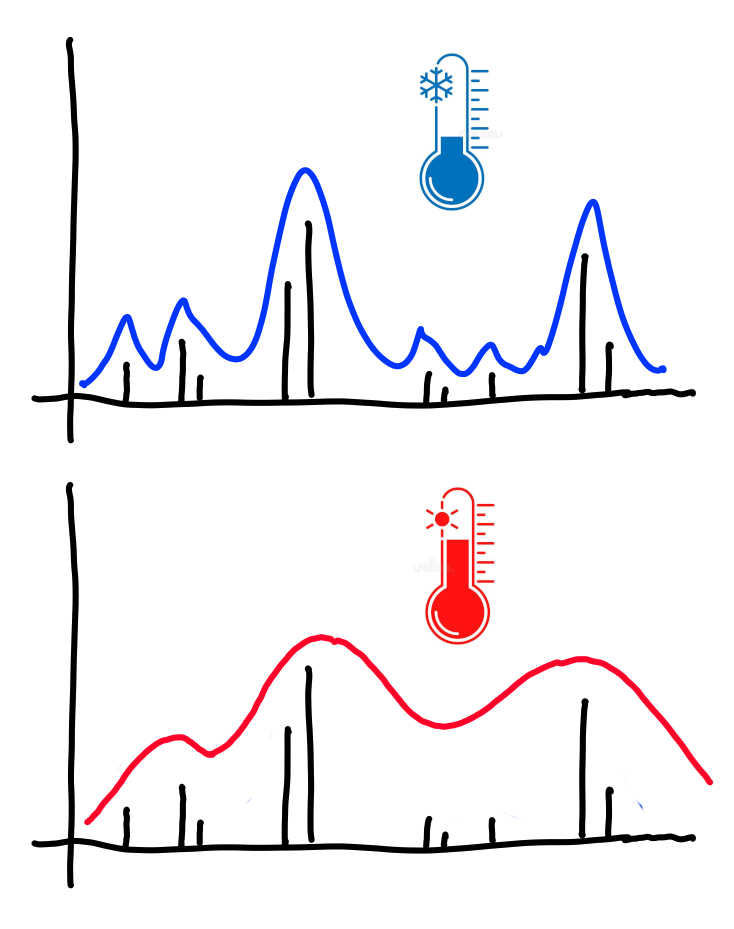
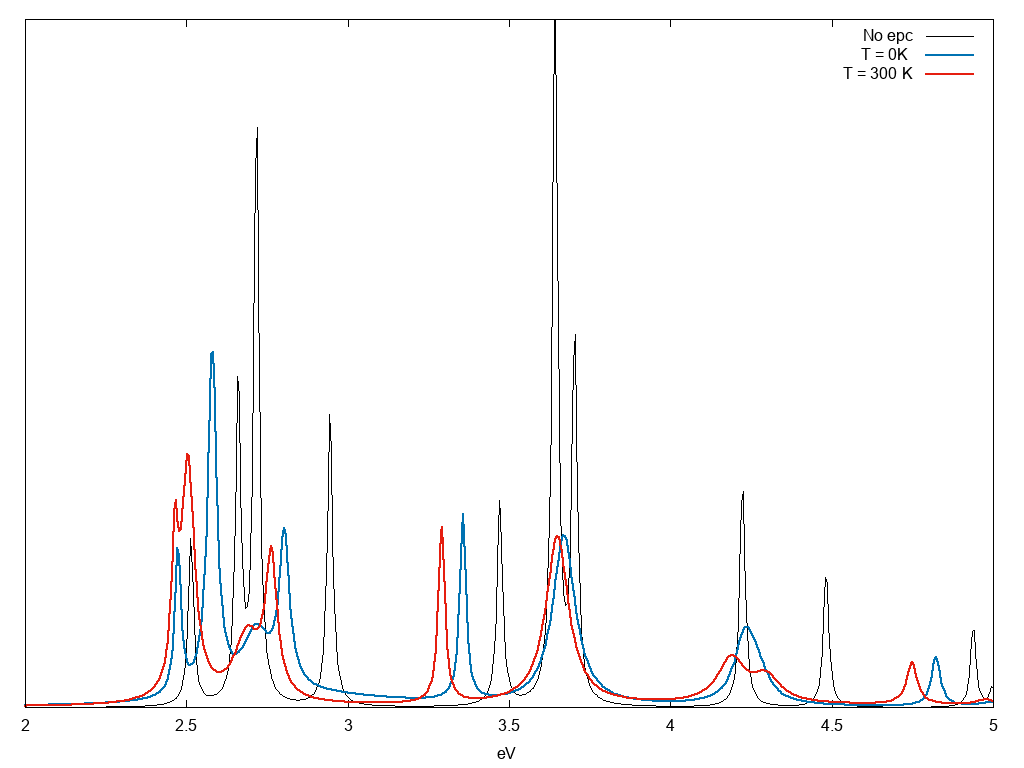
Hereafter the result without and with electron-phonon coupling at two different temperatures:

Absorption of bulk silicon at finite temperature

The temperature effect is clearly visible in the figure.

Bethe-Salpeter at finite temperature (diagonalization solver)

In this section we will calculate the Bethe-Salpeter at finite temperature using the full-BSE.

You can generate the input using the command yambo_ph -X s -o b -k sex -y d -V qp -F yambo.in_BSE 

em1s                             # [R][Xs] Statically Screened Interaction
optics                           # [R] Linear Response optical properties
bss                              # [R] BSE solver
bse                              # [R][BSE] Bethe Salpeter Equation.
dipoles                          # [R] Oscillator strenghts (or dipoles)
DIP_Threads=0                    # [OPENMP/X] Number of threads for dipoles
X_Threads=0                      # [OPENMP/X] Number of threads for response functions
K_Threads=0                      # [OPENMP/BSK] Number of threads for response functions
Chimod= "HARTREE"                # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
BSEmod= "coupling"               # [BSE] resonant/retarded/coupling
BSKmod= "SEX"                    # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
BSSmod= "d"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
BSENGexx=  9257            RL    # [BSK] Exchange components
BSENGBlk=-1                RL    # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)]
#WehCpl                        # [BSK] eh interaction included also in coupling
KfnQPdb= "E W < T0/ndb.QP"       # [EXTQP BSK BSS] Database action
% KfnQP_E
0.500000 | 1.000000 | 1.000000 |        # [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim
%
BSEprop= "abs"                   # [BSS] Can be any among abs/jdos/kerr/magn/dich/photolum/esrt
BSEdips= "none"                  # [BSS] Can be "trace/none" or "xy/xz/yz" to define off-diagonal rotation plane
% BSEQptR
 1 | 1 |                             # [BSK] Transferred momenta range
%
% BSEBands
  2 |  7 |                           # [BSK] Bands range
%
% BEnRange
 0.000000 | 5.000000 |         eV    # [BSS] Energy range
%
% BDmRange
0.010000 | 0.010000 |         eV    # [BSS] Damping range
%
BEnSteps= 1500                   # [BSS] Energy steps
% BLongDir
 1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
%
#WRbsWF                        # [BSS] Write to disk excitonic the WFs
% BndsRnXs
  1 | 12 |                           # [Xs] Polarization function bands
%
NGsBlkXs= 113                RL    # [Xs] Response block size
% LongDrXs
 1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
%
XTermKind= "none"                # [X] X terminator ("none","BG" Bruneval-Gonze)


In this input file we asked Yambo to include finite temperature quasi-particle in the BSE with the line KfnQPdb= "E W < T0/ndb.QP" , notice that we also introduce an additional rigid shift of 0.5 eV to mimic the GW correction with the line 0.500000 | 1.000000 | 1.000000 | \# [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim. You can now run the calculation with the command yambo_ph -F yambo.in_BSE -J T0_BSE
In principle you can calculate the GW correction following the this tutorial and then merge the corresponding ndb.QP database with the one of the electron-phonon coupling using the command ypp -qpdb m. Notice that we changed the BSE type to "coupling" because you need the full Bethe-Salpeter to deal with complex quasi-particles.
Now we do the same calculation at T = 300 K. Copy the previous input file cp yambo.in_BSE yambo.in_BSE_300. Then modify where the code reads the QP database : 

KfnQPdb= "E W < T300/ndb.QP"       # [EXTQP BSK BSS] Database action

Run the command with yambo_ph -F yambo.in_BSE_300 -J T300_BSE
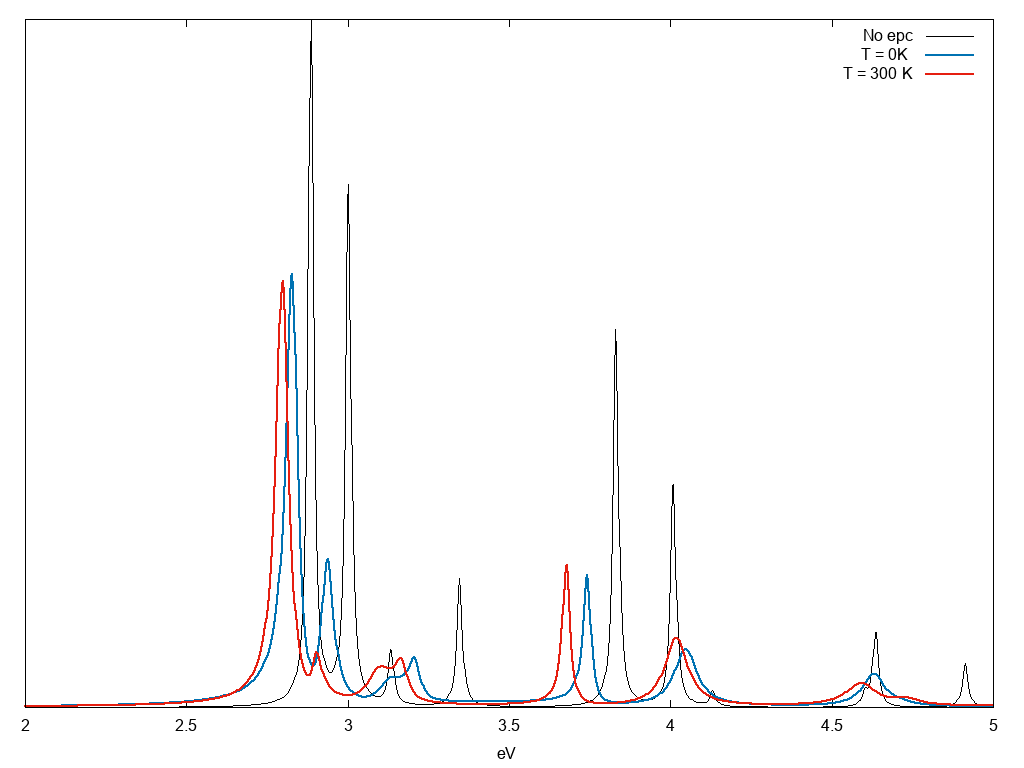
Finally, you should be able to plot the absorption spectra from the outputs in gnuplot : 

 plot 'o-T0_BSE.eps_q1_diago_bse' w l t '0 K', 'o-T300_BSE.eps_q1_diago_bse' w l t '300 K'
Bethe-Salpeter at finite temperature for bulk silicom

Approximations:
In this calculation we have made different approximations:
1) we did not include the renormalization of excitons due to the change of the screening potential W with temperature. Including electron-phonon coupling in the dielectric constant by changing the line XfnQPdb= "none" is unfortunately not enough, for a discussion see ref. [2]
2) The electron-phonon coupling should enter in the BSE through the exciton-phonon matrix elements and not from the single-particle self-energy, as we have done in this tutorial. The approximation used in this tutorial is valid for not too strong bound excitons, and in general it generated a finite life-time also for the lowest exciton in direct materials that is not correct. For a discussion see refs.[3][4][5] and [6].
3) we did not include scattering between exciton and phonons, therefore our results do not contain phonon-assisted absorption peaks, you can include these terms by finite difference displacements see refs. [5].

Result analysis

Results of BSE at finite temperature can be analized in the same way of standard BSE. You can plot exciton binging energy as a function of the temperature, exciton wave-function and so, see Exciton Plot tutorial. For example if you sort exciton with the command ypp_ph -e s -J T0_BSE for the case T=0K, in addition to the exciton energy now you will find its line-width in the files . o-T0_BSE.exc_qpt1_E_sorted and o-T0_BSE.exc_qpt1_I_sorted. 

#
#    Maximum Residual Value = .77136E+05
#   
#    E [ev]             Strength           Index              W [meV]
#
...............
    2.82974172        0.388171151E-1      335.000000         11.9707289
    2.82976580        0.110338017         334.000000         11.9676380
    2.82979798        0.992550552         333.000000         11.9646358
    2.83366466        0.177820283E-2      336.000000         6.12744808
    2.83368802        0.183327938E-3      338.000000         6.12689734
    2.83369708        0.679280609E-3      337.000000         6.12836981
    2.87943292        0.146849517E-3      332.000000         2.51892495
    2.87945318        0.295515812E-3      331.000000         2.51745558
    2.89804840        0.539837289E-3      330.000000         1.42265606
    2.93557525        0.532299697         329.000000         12.5491867
    2.93559408        0.214365616         391.000000         12.5504198
    2.93561029        0.175688639         390.000000         12.5498590
    2.97320676        0.158064649E-3      388.000000         9.35168839
    2.97321057        0.300355150E-4      408.000000         9.35530090
    2.97321224        0.931323011E-4      389.000000         9.35327435
    2.97682190        0.551215744E-4      405.000000         8.87609196

Notice that in the files you will find many excitons with negative energy due the anti-resonant part of the full-BSE.

Excitonic Eliashberg Functions

If you run the BSE and save the excitonic wave-functions (uncomment the flag WRbsWF in the BSE input file), tt is possible to plot the excitonic Eliashberg Functions with the command ypp_ph -e e. For an interpretation of these functions see the discussion in reference [7]

Bethe-Salpeter at finite temperature (inversion solver)

It is possible to take into account complex quasi-particles in the BSE solution by means of the inversion procedure. The idea is to construct an Lo (Eq. 5 of Ref.[1]) that includes the electron-phonon corrections including the imaginary part. In order to generate the input you can type: yambo_ph -X s -o b -k sex -y i -V qp 

em1s                             # [R][Xs] Statically Screened Interaction
optics                           # [R] Linear Response optical properties
bss                              # [R] BSE solver
bse                              # [R][BSE] Bethe Salpeter Equation.
dipoles                          # [R] Oscillator strenghts (or dipoles)
DIP_Threads=0                    # [OPENMP/X] Number of threads for dipoles
X_Threads=0                      # [OPENMP/X] Number of threads for response functions
K_Threads=0                      # [OPENMP/BSK] Number of threads for response functions
Chimod= "HARTREE"                # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
BSEmod= "resonant"               # [BSE] resonant/retarded/coupling
BSKmod= "SEX"                    # [BSE] IP/Hartree/HF/ALDA/SEX/BSfxc
BSSmod= "i"                      # [BSS] (h)aydock/(d)iagonalization/(s)lepc/(i)nversion/(t)ddft`
BSENGexx=  9257            RL    # [BSK] Exchange components
BSENGBlk=-1                RL    # [BSK] Screened interaction block size [if -1 uses all the G-vectors of W(q,G,Gp)]
#WehCpl                        # [BSK] eh interaction included also in coupling
KfnQPdb= "E W < T0/ndb.QP"       # [EXTQP BSK BSS] Database action
KfnQP_INTERP_NN= 1               # [EXTQP BSK BSS] Interpolation neighbours (NN mode)
KfnQP_INTERP_shells= 20.00000    # [EXTQP BSK BSS] Interpolation shells (BOLTZ mode)
KfnQP_DbGd_INTERP_mode= "NN"     # [EXTQP BSK BSS] Interpolation DbGd mode
% KfnQP_E
  0.500000 | 1.000000 | 1.000000 |        # [EXTQP BSK BSS] E parameters  (c/v) eV|adim|adim
%
BSEprop= "abs"                   # [BSS] abs/kerr/magn/dichr trace
% BSEQptR
 1 | 1 |                             # [BSK] Transferred momenta range
%
% BSEBands
   2 |  7 |                           # [BSK] Bands range
%
% BEnRange
  0.00000 | 5.00000 |         eV    # [BSS] Energy range 
%
% BDmRange
  0.010000 | 0.010000 |         eV    # [BSS] Damping range
%
BEnSteps= 1500                    # [BSS] Energy steps
% BLongDir 
 1.000000 | 0.000000 | 0.000000 |        # [BSS] [cc] Electric Field
%
#WRbsWF                        # [BSS] Write to disk excitonic the WFs
XfnQPdb= "none"                  # [EXTQP Xd] Database action
% BndsRnXs
  1 | 12 |                           # [Xs] Polarization function bands
%
NGsBlkXs= 113              RL    # [Xs] Response block size
% LongDrXs
 1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
%
XTermKind= "none"                # [X] X terminator ("none","BG" Bruneval-Gonze)

then if you run the job you will get the spectrum at finite temperature. Notice that with the inversion solver you can choose if you want the BSE with or without the coupling by changing the BSEmod variable. This approach can be combined with double-grid as explained here: Speed up dielectric constant calculations using the double-grid method with Yambo . Yambo automatically will interpolate quasi-particle corrections on the fine grid.
Notice that BSE inversion can become unfeasible for large BSE matrices.

Nota bene: if you use the inversion solver you just get the optical spectra, but you do not have access to the excitonic eigenvalues and eigenvectors and by consequence you cannot plot the excitonic wave-function or print the excitonic Eliashberg functions.

Phonon-assisted density of states

Even if exciton-phonon scattering is not included in the BSE at finite temperature, it is possible to plot the phonon-assisted density of states (DOS) for light emission, defined as:

Phonon-assisted JDOS

where Eql is the energy of the l-exciton at q-momentum, ωqλ is the phonon energy, nB is the Bose function, exciton are weighted with a Boltzamn factor and Emin is the lowest exciton energy in the all BZ. In order to calculate these DOS you need to solve BSE for all the q-points for the lowest excitons, you can use SLEPC library to speed up calculations, then you need a converged phonon calculations. Then you interpolate phonon on a dense phonon grid using matdyn.x utility in QE, and Yambo will interpolate exicton on the same grid. Here we present an example for hBN that is an indirect semiconductor. Running ypp_ph -e p you will get: 

BoseTemp= 50 K    # Bosonic Temperature
excitons                         # [R] Excitonic properties
ph_ass_dos                       # [R] Phonon-assisted DOS
States= "1 - 4"                  # Index of the BS state(s)
PHfreqF= "./bn.freq_54"            # PWscf format file containing the phonon frequencies
% DOSERange
 5.000000 | 5.500000 |         eV    # Energy range
%
DOSESteps= 1000                  # Energy steps
DOS_broad= 0.004        eV    # Broadening of the DOS

where "bn.freq_54" is the file produced by matdyn.x with the input: 

&input
    asr='simple',
    flfrc='bn.fc',
    flfrq='bn.freq_54',
    dos=.true.,
    fldos='bn.dos',
    ndos=2
    nk1=54, nk2=54, nk3=18
/

and the BSE was calculated on a 18x18x6 grid. The final spectra will be:

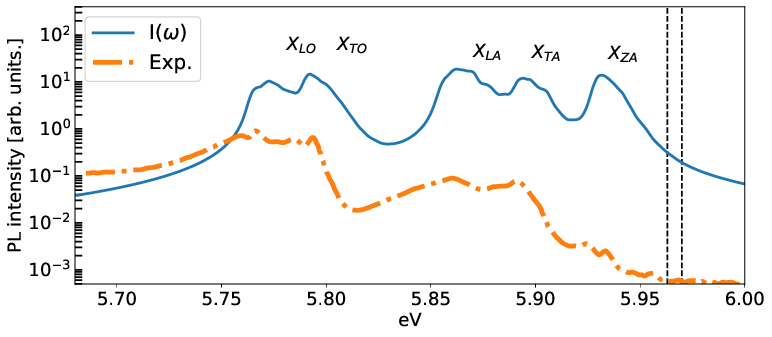
Phonon-assisted JDOS

where the DOS has been shifted to match the experimental peaks. Notice that the peak intensities are complitely off, because of the lack of the exciton-phonon matrix elements.

Links

References

  1. ↑ 1.0 1.1 D. Kammerlander et al. Phys. Rev. B 86, 125203
  2. ↑ L. Adamska and P. Umari, Phys. Rev. B 103, 075201 (2021)
  3. ↑ G. Antonius, S. G. Louie Phys. Rev. B 105, 085111 (2022)
  4. ↑ see Supp. Mat. of Phys. Rev. B 99, 081109(R) (2019)
  5. ↑ 5.0 5.1 F. Paleari, Phd Thesis (2019)
  6. ↑ H. Chen, D. Sangalli, and M. Bernardi Phys. Rev. Lett. 125, 107401 (2020)
  7. ↑ Andrea Marini Phys. Rev. Lett. 101, 106405 (2008)
Retrieved from "https://wiki.yambo-code.eu/wiki/index.php?title=Optical_properties_at_finite_temperature&oldid=5947"