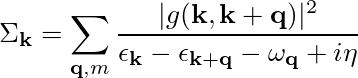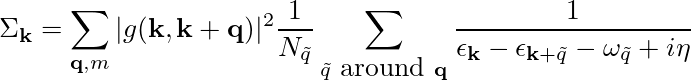Electron Phonon Coupling: Difference between revisions
No edit summary |
|||
| (215 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
Here we show step-by-step how to use [https://www.quantum-espresso.org/ Quantum Espresso] to calculate phonons and electron-phonon matrix-elements on a regular q-grid | [[File:Electron phonon.png|thumb|200px| Electron-phonon coupling]] | ||
Here we show step-by-step how to use [https://www.quantum-espresso.org/ Quantum Espresso] to calculate phonons and electron-phonon matrix-elements on a regular q-grid. | |||
This tutorial is quite | The final aim is to allow Yambo to read them and calculate the temperature-dependent correction to the electronic states. | ||
This tutorial<ref> This tutorial is based on [http://www.attaccalite.com/elena/news/Elena Cannuccia blog]</ref> is quite articulated, take your time to do it patiently. | |||
== Electron-phonon matrix elements == | == Electron-phonon matrix elements == | ||
If you just want to see how Yambo works and leave the database generation for later, or use YamboPy to generate them, <br> | |||
you can skip this section and download ready-made databases: [http://www.attaccalite.com/tutorials_yambo/Si_elph_dbs.tgz Si_elph_dbs.tgz] | |||
In this first section we will explain how to generate electron-phonon matrix elements in Quantum-Espresso, and | |||
Otherwise, in the cloud you need to load the quantum-espresso module: | |||
spack load quantum-espresso | |||
In this first section we will explain how to generate electron-phonon matrix elements in Quantum-Espresso, and how to import them in Yambo. | |||
Calculations will be divided in different folders: | Calculations will be divided in different folders: | ||
* '''pseudo''' the pseudo potential folder | * '''pseudo''' the pseudo potential folder | ||
* '''scf''' for the self-consistent calculation | * '''scf''' for the self-consistent calculation | ||
* '''nscf''' for the non-self-consistent | * '''nscf''' for the non-self-consistent calculation with a larger number of bands | ||
* '''phonon''' for the | * '''phonon''' for the phonon calculations | ||
* '''dvscf''' for the calculation of | * '''dvscf''' for the calculation of the electron-phonon matrix elements | ||
In this tutorial we will show how to calculate electron-phonon induced corrections to the bands and optical properties for bulk silicon. | |||
All input file are availabe in the following tgz file: [http://www.attaccalite.com/tutorials_yambo/si.epc.tgz si.epc.tgz] | |||
===SCF=== | |||
In '''scf''' we run a standard scf calculation using pw.x choosing a large k-grid in such a way to converge density. Do not forget to set <span style="color:green">''force_symmorphic=.true.''</span>, because not symmorphic symmetries are not supported yet in Yambo. Notice that: | |||
a) If you are working with 2D systems, not our case, we have to add the flag <span style="color:green">''assume_isolated="2D"''</span> in such a way correct 2D phonons. | |||
b) If the cell is an <span style="color:green">FCC</span>, set manually the cell parameters by using the flag <span style="color:green">''ibrav=0''</span> in your scf input file. This allows to generate correctly the uniform q grid over which phonons and electron-phonon databases are calculated, for example for Silicon you can use: | |||
&system | |||
...... | |||
ibrav= 0, | |||
celldm(1) =5.132 | |||
..... | |||
/ | |||
..... | |||
CELL_PARAMETERS alat | |||
0.0 1.0 1.0 | |||
1.0 0.0 1.0 | |||
1.0 1.0 0.0 | |||
===NSCF=== | |||
Plug into '''nscf''' folder, and then copy the ${PREFIX}.save folder from '''scf''' to '''nscf''', in the present example just do <span style="color:blue">''cp -r ../scf/si.save ./''</span>. | |||
In the nscf input you have to choose the number of k-points and bands you will use for the electron-phonon coupling and Yambo calculations, in our case we will use a 4x4x4 grid and 12 bands. | |||
===Q-points list === | |||
1. Read the q-points list. In the '''nscf''' folder, enter in the ${PREFIX}.save then run ''p2y'' to read the wave-functions. | |||
2. | 2. Generate the setup file with the command ''yambo_ph -i'' and run the setup. | ||
setup # [R] Initialization | |||
3. Generate the input file to read the electron-phonon matrix elements with the command ''ypp_ph -k q'': | |||
bzgrids # [R] BZ Grid generator | |||
Q_grid # [R] Q-grid analysis | |||
OutputAlat= 0.000000 # [a.u.] Lattice constant used for "alat" ouput format | |||
#NoWeights # Do not print points weight | |||
cooIn= "rlu" # Points coordinates (in) cc/rlu/iku/alat | |||
<span style="color:red">cooOut= "alat"</span> # Points coordinates (out) cc/rlu/iku/alat | |||
<span style="color:red">ListPts </span> # List the internal q/k points also in the parser format | |||
#ExpandPts # Expand the internal q/k points in the BZ | |||
#ForceUserPts # Do not check the correcteness of the user points | |||
%Qpts # Q points list | |||
0.000000| 0.000000| 0.000000| | |||
% | |||
and uncomment the flag '''ListPts''' and q-point coordinates units in '''alat''', the units used by QuantumEspresso. For particular cells, like the FCC, there could be an inconsistency between Yambo and QE definition of alat, in this case you can specify '''OutputAlat''' equal to the '''celldm(1)''' of QE. Then if you run ypp_ph it will generate the list of q-points for the phonon calculations: | |||
..... | ..... | ||
<---> Q-points (IBZ) PW-formatted | |||
0.000000000 0.000000000 0.000000000 1 | |||
0.125000000 0.125000000 -0.125000000 1 | |||
-0.250000000 -0.250000000 0.250000000 1 | |||
0.250000000 0.000000000 0.000000000 1 | |||
0.375000000 0.125000000 -0.125000000 1 | |||
0.000000000 -0.250000000 0.250000000 1 | |||
-0.500000000 0.000000000 0.000000000 1 | |||
-0.500000000 0.250000000 0.000000000 1 | |||
<---> [08] Timing Overview | |||
...... | |||
===Phonons=== | |||
Plug into '''phonon''' directory. You have to copy the self-consistent calculation in this folder | |||
with the command <span style="color:blue">''cp -r ../scf/si.save ./ ''</span>. Then you can prepare an input file for phonons using the q-points list you generated in the previous step multiplied by -1, | |||
the final input will be: | |||
&inputph | &inputph | ||
verbosity = 'high' | verbosity = 'high' | ||
tr2_ph = 1e- | tr2_ph = 1e-12 | ||
prefix = ' | prefix = 'si' | ||
fildvscf = ' | fildvscf = 'si-dvscf' | ||
fildyn = ' | fildyn = 'si.dyn', | ||
electron_phonon = 'dvscf', | electron_phonon = 'dvscf', | ||
epsil = . | epsil = .false. | ||
trans = .true. | trans = .true. | ||
ldisp = .false. | ldisp = .false. | ||
qplot = .true. | qplot = .true. | ||
/ | / | ||
8 | |||
0.000000000 0.000000000 0.000000000 1 | |||
-0.125000000 -0.125000000 0.125000000 1 | |||
0.250000000 0.250000000 -0.250000000 1 | |||
-0.250000000 0.000000000 0.000000000 1 | |||
-0.375000000 -0.125000000 0.125000000 1 | |||
0.000000000 0.250000000 -0.250000000 1 | |||
0.500000000 0.000000000 0.000000000 1 | |||
0.500000000 -0.250000000 0.000000000 1 | |||
Notice that in the tgz file included in this page all input files are already prepared. | |||
===DVSCF=== | |||
Plug into '''dvscf''' folder. From the nscf folder copy density and wave-functions (<span style="color:blue">''cp -r ../nscf/si.save ./''</span>), from the phonon folder copy the dynamical matrices and the dvscf files (<span style="color:blue">''cp -r ../phonon/_ph0 ../phonon/*.dyn* ./''</span>). Then modify the phonon input to generate electron-phonon matrix elements for Yambo, by changing <span style="color:green">epsil = .false.</span>, <span style="color:green">trans = .false.</span> and <span style="color:green">electron_phonon = yambo</span>. You do not need to specify the k-point grid because it is read from the nscf wave-functions. In this way we will not recalculate phonons, but only the electron-phonon matrix elements for the number of bands present in the nscf input file, in our case 8 bands: | |||
&inputph | &inputph | ||
verbosity = 'high' | verbosity = 'high' | ||
tr2_ph = 1e-12 | tr2_ph = 1e-12 | ||
prefix = ' | prefix = 'si' | ||
fildvscf = ' | fildvscf = 'si-dvscf' | ||
fildyn = ' | fildyn = 'si.dyn' | ||
electron_phonon = 'yambo', | electron_phonon = 'yambo', | ||
epsil = . | epsil = .false. | ||
trans = .false. | trans = .false. | ||
ldisp = .false. | ldisp = .false. | ||
qplot = .true. | qplot = .true. | ||
/ | / | ||
8 | |||
0.000000000 0.000000000 0.000000000 1 | |||
-0.125000000 -0.125000000 0.125000000 1 | |||
0.250000000 0.250000000 -0.250000000 1 | |||
-0.250000000 0.000000000 0.000000000 1 | |||
-0.375000000 -0.125000000 0.125000000 1 | |||
0.000000000 0.250000000 -0.250000000 1 | |||
0.500000000 0.000000000 0.000000000 1 | |||
0.500000000 -0.250000000 0.000000000 1 | |||
this run will generate a new folder ''elph_dir'' with all electron-phonon matrix elements in a format compatible with Yambo. | this run will generate a new folder ''elph_dir'' with all electron-phonon matrix elements in a format compatible with Yambo.<br> | ||
<span style="color:red">'''IMPORTANT'''</span>: do not parallelize on k-points in the '''dvscf''' calculation, it is not supported yet!! | |||
===Import in Yambo=== | |||
Now you have to read the electron-phonon matrix elements. Go in the ''dvscf/si.save'' folder, and use ypp_ph to import electron-phonon coupling, by doing ''ypp_ph -g g'' and the PW el-ph folder: | |||
gkkp # [R] gkkp databases | gkkp # [R] gkkp databases | ||
gkkp_db # [R] GKKP database | |||
#GkkpReadBare # Read the bare gkkp | |||
<span style="color:red">DBsPATH= "../elph_dir/" </span> # Path to the PW el-ph databases | <span style="color:red">DBsPATH= "../elph_dir/" </span> # Path to the PW el-ph databases | ||
PHfreqF= "none" # PWscf format file containing the phonon frequencies | PHfreqF= "none" # PWscf format file containing the phonon frequencies | ||
PHmodeF= "none" # PWscf format file containing the phonon modes | PHmodeF= "none" # PWscf format file containing the phonon modes | ||
#GkkpExpand # Expand the gkkp in the whole BZ | #GkkpExpand # Expand the gkkp in the whole BZ | ||
# | #UseQindxB # Use qindx_B to expand gkkp (for testing purposes) | ||
run ypp_ph, and if everything went well you will get in output | run ypp_ph, and if everything went well you will get in output | ||
..... | |||
<---> [06] == Electron-Phonon Databases == | |||
<---> Inspecting databases ...PWscf (dressed)...found 8 Q-points | |||
<---> ELPH databases: phonon frequencies and eigenvectors |########################################| [100%] --(E) --(X) | |||
<---> ELPH databases: K+Q-grid check |########################################| [100%] --(E) --(X) | |||
<---> [07] == Q-points list in the DBS (iku units) == | |||
<---> :: Code generator :PWscf | |||
<---> :: DB Kind :dressed | |||
<---> :: Expanded :no | |||
<---> :: Q-points(read) : 8 | |||
<---> :: Q-points(written) : 8 | |||
<---> :: K-points : 20 | |||
<---> :: Bands : 12 | |||
<---> :: Branches : 6 | |||
<---> :: Uniform sampling :yes | |||
<---> :: Symmetry expanded :no | |||
<---> :: Debye Energy : 63.09927 [meV] | |||
..... | ..... | ||
Notice that Yambo recognized that you are using a regular q-grid: ''Uniform sampling :yes''. | |||
== Quasi-particle band structure == | == Quasi-particle band structure == | ||
The first quantity we will calculate is the correction to the band structure induced by the electron-phonon coupling. In order to generate the corresponding input do | The first quantity we will calculate is the correction to the band structure induced by the electron-phonon coupling. In order to generate the corresponding input do <code>yambo_ph -g n -p fan -c ep -V gen</code>. In the input we require the correction only at gamma point: | ||
dyson # [R] Dyson Equation solver | dyson # [R] Dyson Equation solver | ||
| Line 132: | Line 186: | ||
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy | SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy | ||
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") | DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") | ||
GphBRnge= | % GphBRnge | ||
<span style="color:red"> 1 | 12 | # [ELPH] G[W] bands range</span> | |||
% | |||
% ElPhModes | % ElPhModes | ||
1 | 6 | # [ELPH] Phonon modes included | 1 | 6 | # [ELPH] Phonon modes included | ||
% | % | ||
<span style="color:red">GDamping= 0.0100000 eV # [GW] G[W] damping</span> | |||
RandQpts=0 # [RIM] Number of random q-points in the BZ | RandQpts=0 # [RIM] Number of random q-points in the BZ | ||
#WRgFsq # [ELPH] Dump on file gFsq coefficients | #WRgFsq # [ELPH] Dump on file gFsq coefficients | ||
%QPkrange # [GW] QP generalized Kpoint/Band indices | %QPkrange # [GW] QP generalized Kpoint/Band indices | ||
1| | <span style="color:red">1|8|2|8|</span> | ||
% | % | ||
If you run <code>yambo_ph -J T0</code> you will get correction at zero kelvin to the band structure. | |||
If you run yambo_ph -J T0 you will get correction at zero kelvin to the band structure. You can change the temperature to 300 K by doing: | You can change the temperature to 300 K by doing: | ||
dyson # [R] Dyson Equation solver | dyson # [R] Dyson Equation solver | ||
| Line 149: | Line 206: | ||
Nelectro= 8.000000 # Electrons number | Nelectro= 8.000000 # Electrons number | ||
ElecTemp= 0.000000 eV # Electronic Temperature | ElecTemp= 0.000000 eV # Electronic Temperature | ||
<span style="color:red">BoseTemp= 300.0 | <span style="color:red">BoseTemp= 300.0 Kn </span> # Bosonic Temperature | ||
OccTresh= 0.100000E-4 # Occupation treshold (metallic bands) | OccTresh= 0.100000E-4 # Occupation treshold (metallic bands) | ||
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy | SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy | ||
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") | DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") | ||
GphBRnge= | % GphBRnge | ||
<span style="color:red"> 1 | 12 | # [ELPH] G[W] bands range</span> | |||
% | |||
% ElPhModes | % ElPhModes | ||
1 | 6 | # [ELPH] Phonon modes included | 1 | 6 | # [ELPH] Phonon modes included | ||
% | % | ||
<span style="color:red">GDamping= 0.0100000 eV # [GW] G[W] damping</span> | |||
RandQpts=0 # [RIM] Number of random q-points in the BZ | RandQpts=0 # [RIM] Number of random q-points in the BZ | ||
#WRgFsq # [ELPH] Dump on file gFsq coefficients | #WRgFsq # [ELPH] Dump on file gFsq coefficients | ||
%QPkrange # [GW] QP generalized Kpoint/Band indices | %QPkrange # [GW] QP generalized Kpoint/Band indices | ||
1| | <span style="color:red">1|8|2|8|</span> | ||
% | % | ||
run again | run again <code>yambo_ph -J T300</code> and compare the two output files o-T0.qp and o-T300.qp, to find how much the gap change with the temperature.<br> | ||
Notice that in this calculation we set a small damping factor for the Green function of about 0.01 eV, this value should be of the order of the phonon life-time.<br> | |||
If you repeat the calculation for different temperature you can obtain the trend of the gap vs temperature. The figure below report the Silicon gap at Gamma Point at different temperature obtained in this tutorial. You can recreate the file with the data needed for this plot with the following command line instruction: | |||
for i in 0 50 100 150 200 250 300; do echo -n "$i "; echo "$(grep "^ *1 *5" o-T${i}.qp | awk '{print ($3+$4)}') - $(grep "^ *1 *4" o-T${i}.qp | awk '{print ($3+$4)}')" | bc; done > gap_vs_T.dat | |||
and then in <code>gnuplot</code> type | |||
plot 'gap_vs_T.dat' u 1:2 w lp | |||
<span style="color: | [[File:Si_gap_finite_t.png|600px|center]] | ||
If you uncomment the flag <span style="color:green">WRgFsq</span> the code saves information about the Eliashberg functions that can be plotted using the ''ypp_ph'', see below.<br> | |||
Finally if you add ''-V qp'' in the input generation a new flag appears <span style="color:green">OnMassShell</span>, if you un-comment this flag calculation will be performed in the "on mass shell" approximation, namely the static limit the Quasi-Particle approximation, for a discussion see reference <ref>H. Kawai et al. [https://arxiv.org/abs/1310.2038 Phys. Rev. B '''89''', 085202 (2014)]</ref> | |||
This means that calculation reduces to the static perturbation theory of Allen-Cardona.<br> | |||
Notice that the last column in the quasi-particle file "o.QP" contains the '''quasi-particle width''', that is related to their life-time. You can plot the band structure including this width to get quasi-particle spectra | |||
similar to the one measured in ARPES experiments, see Fig. 2 in ref. <ref> G. Antonius, S. Poncé, E. Lantagne-Hurtubise, G. Auclair, X. Gonze, and M. Côté | |||
[https://arxiv.org/abs/1505.07738 Phys. Rev. B 92, 085137 (2015)] </ref>. | |||
This parameter will be used in the next tutorial on [https://www.yambo-code.org/wiki/index.php?title=Optical_properties_at_finite_temperature optical properties at finite temperature]. | |||
<br><br><span style="color:red"><b>WARNING:</b></span> Yambo average the electron-phonon correction on the degenerate states, please <b>include all degenerate states in your calculations</b>. For example in the silicon case you need correction from the 2nd band to the 8th band. | |||
== Convergence == | == Convergence == | ||
The results of this tutorial are not converged | The results of this tutorial are not converged. This is due to the poor parameters used in this tutorial to make the calculations fast. In order to have converged results, first of all you have to be sure to have converged phonons, in order to do that increase plane-wave cutoff, number of k-points and if necessary reduce ''tr2_ph''. | ||
Then change the | Then change the parameters for the Yambo calculations, increasing the number of '''k''' and '''q''' points and the number of bands. If you want to increase only the number of bands, just repeat the '''nscf''' and '''dvscf''' calculations without recalculate '''phonons'''. In the following section we will describe a smart way to accelerate convergence.<br> | ||
<span style="color:red">Nota bene: </span> At present Yambo neither implements the Fröhlich term at q=0<ref>Carla Verdi and Feliciano Giustino | |||
[https://arxiv.org/abs/1510.06373 Phys. Rev. Lett. '''115''', 176401 (2015)] </ref> nor the quadrupolar correction,<ref>G. Brunin et al. [https://arxiv.org/abs/2002.00628 Phys. Rev. Lett. '''125''', 136601 (2020)]</ref> therefore convergence in polar material can be very slow with the number of q-points. | |||
== Double-grid method for the electron-phonon coupling (only in Yambo 5.x) == | |||
Simplifying at most the matrix elements of the electron-phonon self-energy have the structure: | |||
[[File:Self elph.png|center|Yambo tutorial image | 270px ]] | |||
where we omitted the electronic band and the phonon branches indexes. In order to speed up calculation one can average the denominators on an additional fine grid around each '''q''' points as: | |||
[[File:Formula dbgrid.png|center|Yambo tutorial image| 500px]] | |||
In order to exploit the double-grid tool we need the phonon energies calculated on a fine grid. | |||
<!--If you just want to test the functionality of Yambo you can download here some files with the phononic frequencies already calculated on different silicon grids: [https://www.yambo-code.org/educational/tutorials/files/si_freqs_files.tgz si_freqs_files.tgz] <br> !--> | |||
You generate them by following the instructions below. | |||
'''<span style="color:red">Concerning the school, we suggest to use the precomputed frequencies provided above.</span>''' | |||
For a general tutorial on phonon calculation with Quantum Espresso you can have a look at [https://www.quantum-espresso.org/wp-content/uploads/phonons_tutorial_shanghai1.pdf Hands on phonons].<br> | |||
Starting from a well converged phonon calculation ''matdyn.x'' can interpolate phonon dispersion on a given q-sampling (for example a regular 14x14x14 grid, as shown in the input file below) and give the desired phonon energies. | |||
&input | |||
asr='simple', | |||
flfrc='si.fc', | |||
flfrq='si.freq', | |||
dos=.true., | |||
fldos='si.dos', | |||
deltaE=1.d0, | |||
nk1=14, nk2=14, nk3=14 | |||
/ | |||
Alternatively you can generate a random q-sampling using Yambo (''ypp -k r'') and insert the corresponding q points list into a matdyn file. | |||
Once you generated the phonon energies you can read them with the command <code>ypp_ph -g d</code> (in this example we read the 12x12x12 double grid): | |||
gkkp # [R] gkkp databases | |||
gkkp_dg # [R] GKKP double grid | |||
<span style="color:red">PHfreqF= "si.freq_12"</span> # PWscf format file containing the phonon frequencies | |||
PHmodeF= "none" # PWscf format file containing the phonon modes | |||
FineGd_mode= "mixed" # Fine Grid mode. Symmetry expanded, unexpanded or mixed. | |||
#SkipBorderPts # Skip points in the Fine Grid that are on the surface of coarse gride smal BZ`s | |||
EkplusQmode= "interp" # E(k+q) energies calculation mode (interp | dftp ) | |||
#TestPHDGrid # Test double-grid: set all values of the fine grid equal to the couse ones | |||
then run <code>ypp_ph</code> an it will generate a new file ''SAVE/ndb.PH_Double_Grid''. <br> | |||
In the calculation the new phonon energies will be expanded | |||
using the symmetries of the systems, while the electronic energies at '''k+q''' will be interpolated using a smooth Fourier interpolation<ref>Warren E. Pickett, Henry Krakauer, and Philip B. Allen, | |||
Phys. Rev. B '''38''', 2721(1988)</ref>. | |||
Now we go back to our ''yambo.in'' input file and repeat the calculations. The double grid will be automatically accounted for. | |||
We reset the temperature to <code>BoseTemp= 0.0 Kn # Bosonic Temperature</code> and run the calculation in a new directory: | |||
yambo_ph -J T0_12 | |||
We can repeat the process for all the other double grids provided (12x12x12, 24x24x24, 36x36x36, 48x48x48) and check the band convergence to determine which double grid we will use. This takes time, so you may skip it and go on with the tutorial. | |||
'''In fact, the best strategy to converge electron-phonon coupling calculations is to ''first'' converge the double-grid for a fixed coarse main grid, and ''second'', once the final double-grid has been found, converge the main grid itself. <span style="color:red">This is a process that takes time since it requires repeating the electron-phonon matrix element calculations each time the main grid is changed, therefore you are not supposed to do it for this tutorial.</span>''' Hereafter we provide an example of Silicon band gap correction convergence versus the number of '''q'''-points in the main grid, using a double-grid with 4096 random '''q'''-points. | |||
[[File:Gap conv.png|center|Yambo tutorial image | 750px]] | |||
The double-grid implementation is described in this paper<ref>Double-grid for the electron-phonon problem, (to be published) E. Cannuccia, C. Attaccalite and V. Olevano (2022)</ref>. | |||
<!-- | |||
== Electron-phonon coupling using different '''q''' and '''k''' grids (only in Yambo 5.x) == | |||
NOT WORKING!!!!! | |||
The procedure to create electron-phonon matrix elements and import them in Yambo is quite complicated. | |||
For this reason in Yambo 5.x we decided to simplify this kind of calculations. | |||
Now you can generate the '''q''' grid independently from the '''k''' grid. | |||
You follow the previous steps to generate EPC matrix elements but in the phonon/dvscf input file | |||
you specify the standard QE q-grid: | |||
&inputph | |||
verbosity = 'high' | |||
tr2_ph = 1e-12h | |||
prefix = 'si' | |||
fildvscf = 'si-dvscf' | |||
fildyn = 'si.dyn', | |||
electron_phonon = 'dvscf', | |||
epsil = .true. | |||
trans = .true. | |||
<span style="color:red"> ldisp = .true.</span> | |||
<span style="color:red"> nq1=6, nq2=6, nq3=2</span> | |||
/ | |||
then when you read the electron-phonon matrix elements you need to add the flag | |||
gkkp # [R] gkkp databases | |||
gkkp_db # [R] GKKP database | |||
#GkkpReadBare # Read the bare gkkp | |||
DBsPATH= "../elph_dir/" # Path to the PW el-ph databases | |||
PHfreqF= "none" # PWscf format file containing the phonon frequencies | |||
PHmodeF= "none" # PWscf format file containing the phonon modes | |||
<span style="color:red">GkkpExpand </span> # Expand the gkkp in the whole BZ | |||
In this way you can converge '''q''' grid independently for the '''k''' one. This is important because in general a larger set of q-points | |||
is required to have converged results compared to the k-one. Add the flag "-V ph" in the input generation for the electron-phonon self-energy and set: | |||
<span style="color:red">GkkpDB= "gkkp_expanded" </span> # [ELPH] GKKP database (gkkp | gkkp_expanded | genFroh ) | |||
Notice that the double-grid works also with k/q different grids. | |||
--> | |||
== Miscellaneous and post-processing == | == Miscellaneous and post-processing == | ||
'''Automatic generation of electron-phonon matrix elements'''<br> | |||
Getting electron-phonon matrix elements from QuantumEspresso to Yambo is a complicated process, <br> | |||
we advice you to create a script to automatize the procedure, here an example of a bash script for the silicon case: [https://www.yambo-code.org/educational/tutorials/files/SILICON_CONV.tgz SILICON-SCRIPT]. | |||
There are a list of utilities to analyze electron-phonon coupling results: | There are a list of utilities to analyze electron-phonon coupling results: | ||
'''Phonon density of states'''<br> | |||
You can plot phonon density of states with the command: ''ypp_ph -p d''. In order to get a nice plot set in the input | |||
phonons # [R] Phononic properties | |||
dos # [R] DOS | |||
<span style="color:red">PhBroad= 0.0005000 eV</span> # Phonon broadening (Eliashberg & DOS) | |||
<span style="color:red">PhStps=1000 </span> # Energy steps | |||
The we can analyse the phonon DOS of our previous <code>T0</code> calculation by doing: | |||
ypp_ph -J T0 | |||
We get the output file ''o-T0.ph_dos'' which we can plot. | |||
Notice that this is an easy quantity to check for the convergence in q-points. | |||
[[File:Ph_dos.png|600px|center| Phonon Density of States]] | |||
'''Eliashberg Functions'''<br> | |||
You can plot Eliashberg functions<ref>F. Marsiglio, J.P. Carbotte [https://arxiv.org/abs/cond-mat/0106143 Electron - Phonon Superconductivity]</ref> for both electrons and excitons. In order to plot Eliashberg functions you must have calculated Quasi-Particle correction with the flag <span style="color:green">WRgFsq</span>, see above. If you didn't do that, please rerun the <code>yambo_ph</code> calculation (if you use the directory of a previous calculation to do this, remove or rename the ''ndb.QP'' file). | |||
The command <code>ypp_ph -s e</code> generate the input for the electronic Eliashberg functions: | |||
electrons # [R] Electronic properties | |||
eliashberg # [R] Eliashberg | |||
<span style="color:red">PhBroad= 0.0010000 eV </span> # Phonon broadening (Eliashberg & DOS) | |||
<span style="color:red">PhStps= 200 </span> # Energy steps | |||
%QPkrange # generalized Kpoint/Band indices | |||
<span style="color:red"> 1|1|2|8| </span> | |||
% | |||
We can run the postprocessing as | |||
ypp_ph -J T0 | |||
Tn this example we plot Eliashberg functions for the top valence and bottom conduction band at the Gamma point: | |||
[[File:Eliashberg functions.png|600px|center| Eliashberg functions]] | |||
For a discussion on how to interprete Eliashberg functions and use them to understand the different phonon contribution you can have a look to ref.<ref>E. Cannuccia and A. Gali | |||
[https://arxiv.org/abs/1907.06089 Phys. Rev. Materials 4, 014601 (2020)] </ref> | |||
'''Atomic displacement amplitudes'''<br> | |||
Running <code>ypp_ph -p a</code> will plot the atomic displacement for each atom in the cell along each direction. | |||
''' Other variables in the input files '''<br> | |||
In the input files of the present tutorial there are other relevant variables which we did not use. | |||
In particular <code>GkkpExpand</code> is used to expand the electron-phonon matrix elements over the full Brillouin zone in both k-space and q-space. | |||
==Links== | |||
* Back to [[ICTP 2022#Tutorials]] | |||
==References== | ==References== | ||
<references /> | <references /> | ||
Latest revision as of 09:34, 30 November 2023
Here we show step-by-step how to use Quantum Espresso to calculate phonons and electron-phonon matrix-elements on a regular q-grid. The final aim is to allow Yambo to read them and calculate the temperature-dependent correction to the electronic states. This tutorial[1] is quite articulated, take your time to do it patiently.
Electron-phonon matrix elements
If you just want to see how Yambo works and leave the database generation for later, or use YamboPy to generate them,
you can skip this section and download ready-made databases: Si_elph_dbs.tgz
Otherwise, in the cloud you need to load the quantum-espresso module:
spack load quantum-espresso
In this first section we will explain how to generate electron-phonon matrix elements in Quantum-Espresso, and how to import them in Yambo. Calculations will be divided in different folders:
- pseudo the pseudo potential folder
- scf for the self-consistent calculation
- nscf for the non-self-consistent calculation with a larger number of bands
- phonon for the phonon calculations
- dvscf for the calculation of the electron-phonon matrix elements
In this tutorial we will show how to calculate electron-phonon induced corrections to the bands and optical properties for bulk silicon. All input file are availabe in the following tgz file: si.epc.tgz
SCF
In scf we run a standard scf calculation using pw.x choosing a large k-grid in such a way to converge density. Do not forget to set force_symmorphic=.true., because not symmorphic symmetries are not supported yet in Yambo. Notice that:
a) If you are working with 2D systems, not our case, we have to add the flag assume_isolated="2D" in such a way correct 2D phonons.
b) If the cell is an FCC, set manually the cell parameters by using the flag ibrav=0 in your scf input file. This allows to generate correctly the uniform q grid over which phonons and electron-phonon databases are calculated, for example for Silicon you can use:
&system ...... ibrav= 0, celldm(1) =5.132 ..... / ..... CELL_PARAMETERS alat 0.0 1.0 1.0 1.0 0.0 1.0 1.0 1.0 0.0
NSCF
Plug into nscf folder, and then copy the ${PREFIX}.save folder from scf to nscf, in the present example just do cp -r ../scf/si.save ./. In the nscf input you have to choose the number of k-points and bands you will use for the electron-phonon coupling and Yambo calculations, in our case we will use a 4x4x4 grid and 12 bands.
Q-points list
1. Read the q-points list. In the nscf folder, enter in the ${PREFIX}.save then run p2y to read the wave-functions.
2. Generate the setup file with the command yambo_ph -i and run the setup.
setup # [R] Initialization
3. Generate the input file to read the electron-phonon matrix elements with the command ypp_ph -k q:
bzgrids # [R] BZ Grid generator Q_grid # [R] Q-grid analysis OutputAlat= 0.000000 # [a.u.] Lattice constant used for "alat" ouput format #NoWeights # Do not print points weight cooIn= "rlu" # Points coordinates (in) cc/rlu/iku/alat cooOut= "alat" # Points coordinates (out) cc/rlu/iku/alat ListPts # List the internal q/k points also in the parser format #ExpandPts # Expand the internal q/k points in the BZ #ForceUserPts # Do not check the correcteness of the user points %Qpts # Q points list 0.000000| 0.000000| 0.000000| %
and uncomment the flag ListPts and q-point coordinates units in alat, the units used by QuantumEspresso. For particular cells, like the FCC, there could be an inconsistency between Yambo and QE definition of alat, in this case you can specify OutputAlat equal to the celldm(1) of QE. Then if you run ypp_ph it will generate the list of q-points for the phonon calculations:
.....
<---> Q-points (IBZ) PW-formatted
0.000000000 0.000000000 0.000000000 1
0.125000000 0.125000000 -0.125000000 1
-0.250000000 -0.250000000 0.250000000 1
0.250000000 0.000000000 0.000000000 1
0.375000000 0.125000000 -0.125000000 1
0.000000000 -0.250000000 0.250000000 1
-0.500000000 0.000000000 0.000000000 1
-0.500000000 0.250000000 0.000000000 1
<---> [08] Timing Overview
......
Phonons
Plug into phonon directory. You have to copy the self-consistent calculation in this folder with the command cp -r ../scf/si.save ./ . Then you can prepare an input file for phonons using the q-points list you generated in the previous step multiplied by -1, the final input will be:
&inputph
verbosity = 'high'
tr2_ph = 1e-12
prefix = 'si'
fildvscf = 'si-dvscf'
fildyn = 'si.dyn',
electron_phonon = 'dvscf',
epsil = .false.
trans = .true.
ldisp = .false.
qplot = .true.
/
8
0.000000000 0.000000000 0.000000000 1
-0.125000000 -0.125000000 0.125000000 1
0.250000000 0.250000000 -0.250000000 1
-0.250000000 0.000000000 0.000000000 1
-0.375000000 -0.125000000 0.125000000 1
0.000000000 0.250000000 -0.250000000 1
0.500000000 0.000000000 0.000000000 1
0.500000000 -0.250000000 0.000000000 1
Notice that in the tgz file included in this page all input files are already prepared.
DVSCF
Plug into dvscf folder. From the nscf folder copy density and wave-functions (cp -r ../nscf/si.save ./), from the phonon folder copy the dynamical matrices and the dvscf files (cp -r ../phonon/_ph0 ../phonon/*.dyn* ./). Then modify the phonon input to generate electron-phonon matrix elements for Yambo, by changing epsil = .false., trans = .false. and electron_phonon = yambo. You do not need to specify the k-point grid because it is read from the nscf wave-functions. In this way we will not recalculate phonons, but only the electron-phonon matrix elements for the number of bands present in the nscf input file, in our case 8 bands:
&inputph
verbosity = 'high'
tr2_ph = 1e-12
prefix = 'si'
fildvscf = 'si-dvscf'
fildyn = 'si.dyn'
electron_phonon = 'yambo',
epsil = .false.
trans = .false.
ldisp = .false.
qplot = .true.
/
8
0.000000000 0.000000000 0.000000000 1
-0.125000000 -0.125000000 0.125000000 1
0.250000000 0.250000000 -0.250000000 1
-0.250000000 0.000000000 0.000000000 1
-0.375000000 -0.125000000 0.125000000 1
0.000000000 0.250000000 -0.250000000 1
0.500000000 0.000000000 0.000000000 1
0.500000000 -0.250000000 0.000000000 1
this run will generate a new folder elph_dir with all electron-phonon matrix elements in a format compatible with Yambo.
IMPORTANT: do not parallelize on k-points in the dvscf calculation, it is not supported yet!!
Import in Yambo
Now you have to read the electron-phonon matrix elements. Go in the dvscf/si.save folder, and use ypp_ph to import electron-phonon coupling, by doing ypp_ph -g g and the PW el-ph folder:
gkkp # [R] gkkp databases
gkkp_db # [R] GKKP database
#GkkpReadBare # Read the bare gkkp
DBsPATH= "../elph_dir/" # Path to the PW el-ph databases
PHfreqF= "none" # PWscf format file containing the phonon frequencies
PHmodeF= "none" # PWscf format file containing the phonon modes
#GkkpExpand # Expand the gkkp in the whole BZ
#UseQindxB # Use qindx_B to expand gkkp (for testing purposes)
run ypp_ph, and if everything went well you will get in output
..... <---> [06] == Electron-Phonon Databases == <---> Inspecting databases ...PWscf (dressed)...found 8 Q-points <---> ELPH databases: phonon frequencies and eigenvectors |########################################| [100%] --(E) --(X) <---> ELPH databases: K+Q-grid check |########################################| [100%] --(E) --(X) <---> [07] == Q-points list in the DBS (iku units) == <---> :: Code generator :PWscf <---> :: DB Kind :dressed <---> :: Expanded :no <---> :: Q-points(read) : 8 <---> :: Q-points(written) : 8 <---> :: K-points : 20 <---> :: Bands : 12 <---> :: Branches : 6 <---> :: Uniform sampling :yes <---> :: Symmetry expanded :no <---> :: Debye Energy : 63.09927 [meV] .....
Notice that Yambo recognized that you are using a regular q-grid: Uniform sampling :yes.
Quasi-particle band structure
The first quantity we will calculate is the correction to the band structure induced by the electron-phonon coupling. In order to generate the corresponding input do yambo_ph -g n -p fan -c ep -V gen. In the input we require the correction only at gamma point:
dyson # [R] Dyson Equation solver
gw0 # [R] GW approximation
el_ph_corr # [R] Electron-Phonon Correlation
Nelectro= 8.000000 # Electrons number
ElecTemp= 0.000000 eV # Electronic Temperature
BoseTemp= 0.000000 eV # Bosonic Temperature
OccTresh= 0.100000E-4 # Occupation treshold (metallic bands)
SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy
DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g")
% GphBRnge
1 | 12 | # [ELPH] G[W] bands range
%
% ElPhModes
1 | 6 | # [ELPH] Phonon modes included
%
GDamping= 0.0100000 eV # [GW] G[W] damping
RandQpts=0 # [RIM] Number of random q-points in the BZ
#WRgFsq # [ELPH] Dump on file gFsq coefficients
%QPkrange # [GW] QP generalized Kpoint/Band indices
1|8|2|8|
%
If you run yambo_ph -J T0 you will get correction at zero kelvin to the band structure.
You can change the temperature to 300 K by doing:
dyson # [R] Dyson Equation solver gw0 # [R] GW approximation el_ph_corr # [R] Electron-Phonon Correlation Nelectro= 8.000000 # Electrons number ElecTemp= 0.000000 eV # Electronic Temperature BoseTemp= 300.0 Kn # Bosonic Temperature OccTresh= 0.100000E-4 # Occupation treshold (metallic bands) SE_Threads=0 # [OPENMP/GW] Number of threads for self-energy DysSolver= "n" # [GW] Dyson Equation solver ("n","s","g") % GphBRnge 1 | 12 | # [ELPH] G[W] bands range % % ElPhModes 1 | 6 | # [ELPH] Phonon modes included % GDamping= 0.0100000 eV # [GW] G[W] damping RandQpts=0 # [RIM] Number of random q-points in the BZ #WRgFsq # [ELPH] Dump on file gFsq coefficients %QPkrange # [GW] QP generalized Kpoint/Band indices 1|8|2|8| %
run again yambo_ph -J T300 and compare the two output files o-T0.qp and o-T300.qp, to find how much the gap change with the temperature.
Notice that in this calculation we set a small damping factor for the Green function of about 0.01 eV, this value should be of the order of the phonon life-time.
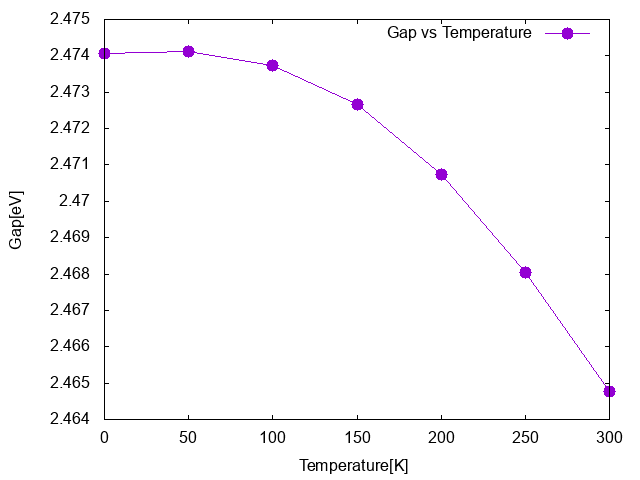
If you repeat the calculation for different temperature you can obtain the trend of the gap vs temperature. The figure below report the Silicon gap at Gamma Point at different temperature obtained in this tutorial. You can recreate the file with the data needed for this plot with the following command line instruction:
for i in 0 50 100 150 200 250 300; do echo -n "$i "; echo "$(grep "^ *1 *5" o-T${i}.qp | awk '{print ($3+$4)}') - $(grep "^ *1 *4" o-T${i}.qp | awk '{print ($3+$4)}')" | bc; done > gap_vs_T.dat
and then in gnuplot type
plot 'gap_vs_T.dat' u 1:2 w lp
If you uncomment the flag WRgFsq the code saves information about the Eliashberg functions that can be plotted using the ypp_ph, see below.
Finally if you add -V qp in the input generation a new flag appears OnMassShell, if you un-comment this flag calculation will be performed in the "on mass shell" approximation, namely the static limit the Quasi-Particle approximation, for a discussion see reference [2]
This means that calculation reduces to the static perturbation theory of Allen-Cardona.
Notice that the last column in the quasi-particle file "o.QP" contains the quasi-particle width, that is related to their life-time. You can plot the band structure including this width to get quasi-particle spectra
similar to the one measured in ARPES experiments, see Fig. 2 in ref. [3].
This parameter will be used in the next tutorial on optical properties at finite temperature.
WARNING: Yambo average the electron-phonon correction on the degenerate states, please include all degenerate states in your calculations. For example in the silicon case you need correction from the 2nd band to the 8th band.
Convergence
The results of this tutorial are not converged. This is due to the poor parameters used in this tutorial to make the calculations fast. In order to have converged results, first of all you have to be sure to have converged phonons, in order to do that increase plane-wave cutoff, number of k-points and if necessary reduce tr2_ph.
Then change the parameters for the Yambo calculations, increasing the number of k and q points and the number of bands. If you want to increase only the number of bands, just repeat the nscf and dvscf calculations without recalculate phonons. In the following section we will describe a smart way to accelerate convergence.
Nota bene: At present Yambo neither implements the Fröhlich term at q=0[4] nor the quadrupolar correction,[5] therefore convergence in polar material can be very slow with the number of q-points.
Double-grid method for the electron-phonon coupling (only in Yambo 5.x)
Simplifying at most the matrix elements of the electron-phonon self-energy have the structure:
where we omitted the electronic band and the phonon branches indexes. In order to speed up calculation one can average the denominators on an additional fine grid around each q points as:
In order to exploit the double-grid tool we need the phonon energies calculated on a fine grid. You generate them by following the instructions below.
Concerning the school, we suggest to use the precomputed frequencies provided above.
For a general tutorial on phonon calculation with Quantum Espresso you can have a look at Hands on phonons.
Starting from a well converged phonon calculation matdyn.x can interpolate phonon dispersion on a given q-sampling (for example a regular 14x14x14 grid, as shown in the input file below) and give the desired phonon energies.
&input
asr='simple',
flfrc='si.fc',
flfrq='si.freq',
dos=.true.,
fldos='si.dos',
deltaE=1.d0,
nk1=14, nk2=14, nk3=14
/
Alternatively you can generate a random q-sampling using Yambo (ypp -k r) and insert the corresponding q points list into a matdyn file.
Once you generated the phonon energies you can read them with the command ypp_ph -g d (in this example we read the 12x12x12 double grid):
gkkp # [R] gkkp databases
gkkp_dg # [R] GKKP double grid
PHfreqF= "si.freq_12" # PWscf format file containing the phonon frequencies
PHmodeF= "none" # PWscf format file containing the phonon modes
FineGd_mode= "mixed" # Fine Grid mode. Symmetry expanded, unexpanded or mixed.
#SkipBorderPts # Skip points in the Fine Grid that are on the surface of coarse gride smal BZ`s
EkplusQmode= "interp" # E(k+q) energies calculation mode (interp | dftp )
#TestPHDGrid # Test double-grid: set all values of the fine grid equal to the couse ones
then run ypp_ph an it will generate a new file SAVE/ndb.PH_Double_Grid.
In the calculation the new phonon energies will be expanded
using the symmetries of the systems, while the electronic energies at k+q will be interpolated using a smooth Fourier interpolation[6].
Now we go back to our yambo.in input file and repeat the calculations. The double grid will be automatically accounted for.
We reset the temperature to BoseTemp= 0.0 Kn # Bosonic Temperature and run the calculation in a new directory:
yambo_ph -J T0_12
We can repeat the process for all the other double grids provided (12x12x12, 24x24x24, 36x36x36, 48x48x48) and check the band convergence to determine which double grid we will use. This takes time, so you may skip it and go on with the tutorial.
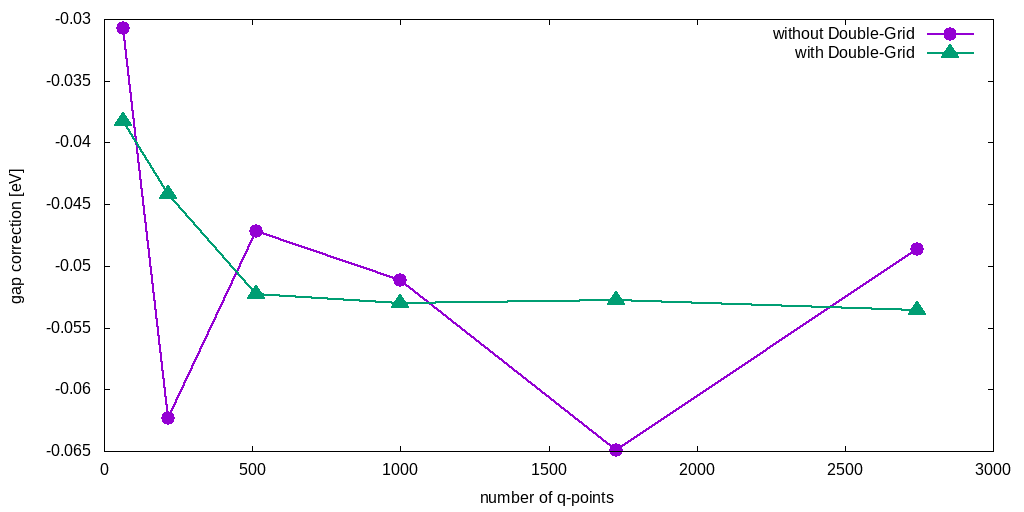
In fact, the best strategy to converge electron-phonon coupling calculations is to first converge the double-grid for a fixed coarse main grid, and second, once the final double-grid has been found, converge the main grid itself. This is a process that takes time since it requires repeating the electron-phonon matrix element calculations each time the main grid is changed, therefore you are not supposed to do it for this tutorial. Hereafter we provide an example of Silicon band gap correction convergence versus the number of q-points in the main grid, using a double-grid with 4096 random q-points.
The double-grid implementation is described in this paper[7].
Miscellaneous and post-processing
Automatic generation of electron-phonon matrix elements
Getting electron-phonon matrix elements from QuantumEspresso to Yambo is a complicated process,
we advice you to create a script to automatize the procedure, here an example of a bash script for the silicon case: SILICON-SCRIPT.
There are a list of utilities to analyze electron-phonon coupling results:
Phonon density of states
You can plot phonon density of states with the command: ypp_ph -p d. In order to get a nice plot set in the input
phonons # [R] Phononic properties dos # [R] DOS PhBroad= 0.0005000 eV # Phonon broadening (Eliashberg & DOS) PhStps=1000 # Energy steps
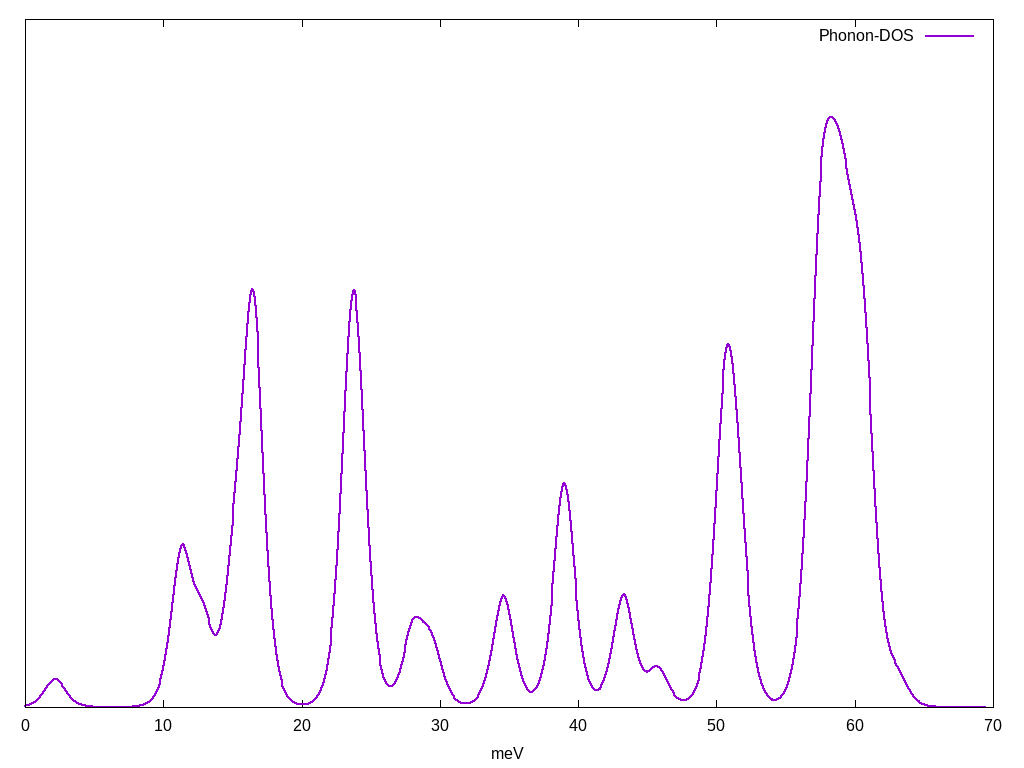
The we can analyse the phonon DOS of our previous T0 calculation by doing:
ypp_ph -J T0
We get the output file o-T0.ph_dos which we can plot. Notice that this is an easy quantity to check for the convergence in q-points.
Eliashberg Functions
You can plot Eliashberg functions[8] for both electrons and excitons. In order to plot Eliashberg functions you must have calculated Quasi-Particle correction with the flag WRgFsq, see above. If you didn't do that, please rerun the yambo_ph calculation (if you use the directory of a previous calculation to do this, remove or rename the ndb.QP file).
The command ypp_ph -s e generate the input for the electronic Eliashberg functions:
electrons # [R] Electronic properties eliashberg # [R] Eliashberg PhBroad= 0.0010000 eV # Phonon broadening (Eliashberg & DOS) PhStps= 200 # Energy steps %QPkrange # generalized Kpoint/Band indices 1|1|2|8| %
We can run the postprocessing as
ypp_ph -J T0
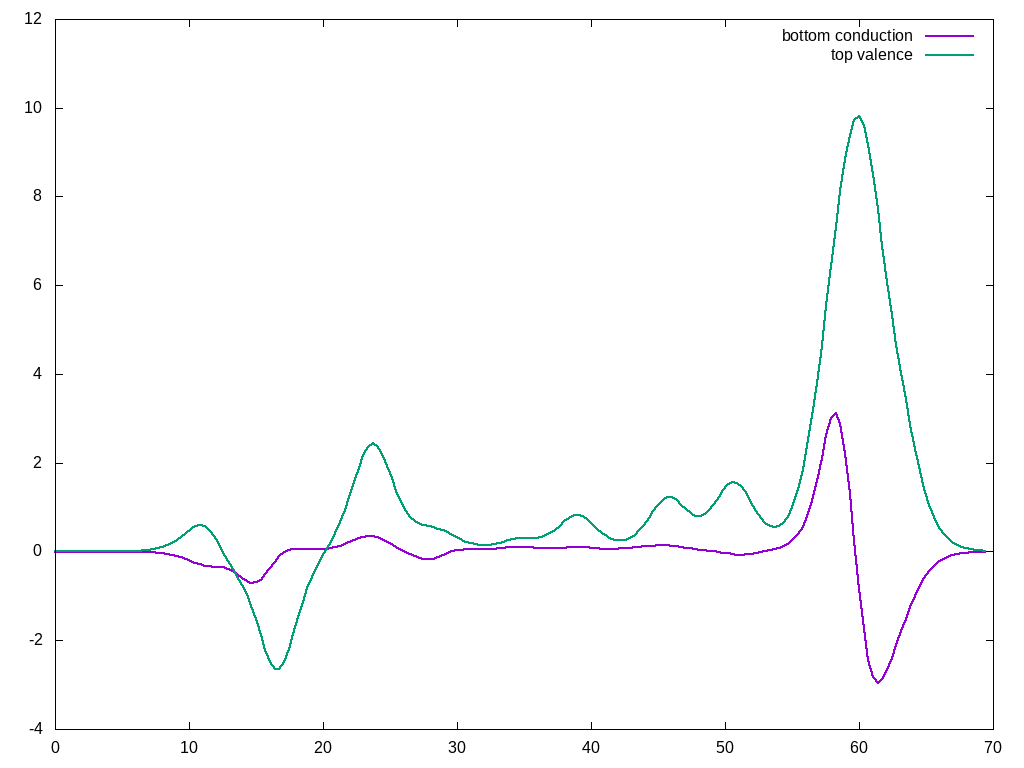
Tn this example we plot Eliashberg functions for the top valence and bottom conduction band at the Gamma point:
For a discussion on how to interprete Eliashberg functions and use them to understand the different phonon contribution you can have a look to ref.[9]
Atomic displacement amplitudes
Running ypp_ph -p a will plot the atomic displacement for each atom in the cell along each direction.
Other variables in the input files
In the input files of the present tutorial there are other relevant variables which we did not use.
In particular GkkpExpand is used to expand the electron-phonon matrix elements over the full Brillouin zone in both k-space and q-space.
Links
- Back to ICTP 2022#Tutorials
References
- ↑ This tutorial is based on Cannuccia blog
- ↑ H. Kawai et al. Phys. Rev. B 89, 085202 (2014)
- ↑ G. Antonius, S. Poncé, E. Lantagne-Hurtubise, G. Auclair, X. Gonze, and M. Côté Phys. Rev. B 92, 085137 (2015)
- ↑ Carla Verdi and Feliciano Giustino Phys. Rev. Lett. 115, 176401 (2015)
- ↑ G. Brunin et al. Phys. Rev. Lett. 125, 136601 (2020)
- ↑ Warren E. Pickett, Henry Krakauer, and Philip B. Allen, Phys. Rev. B 38, 2721(1988)
- ↑ Double-grid for the electron-phonon problem, (to be published) E. Cannuccia, C. Attaccalite and V. Olevano (2022)
- ↑ F. Marsiglio, J.P. Carbotte Electron - Phonon Superconductivity
- ↑ E. Cannuccia and A. Gali Phys. Rev. Materials 4, 014601 (2020)