Real time Bethe-Salpeter Equation (TDSE): Difference between revisions

From The Yambo Project
Jump to navigation Jump to search
 
(32 intermediate revisions by 2 users not shown)
Line 1: Line 1:
==Background==
==Introduction==
In Yambo we combined static screened self-energy derived by means of Non-equilibrium Green's function with Modern Theory of Polarization (Ref. <ref name="agm">[https://arxiv.org/abs/1109.2424 C. Attaccalite, M. Grüning, and A. Marini PRB '''84''', 245110 (2011)]</ref>  and <ref name="prb88"> [https://arxiv.org/abs/1309.4012 C. Attaccalite, M. Grüning, Phys. Rev. B '''88''', 235113 (2013)]</ref>)


[[File:Formula tdse.png|center|400px|Time-Dependent Schrödinger Equation]]
This tutorial will show how to perform a real-time calculation with Yambo on hBN monolayer. We will go through different approximations for the many body self--energy (HXC potential in the yambo language) up to the HSEX approximation which captures the physics of the exciton. For approximations local in space, like "TD-HARTREE" and "TD-DFT", the HXC potential can be evaluated directly during the simulation from real space quantities. On the contrary for approximations non local in space, one first need to compute the "real time collisions".


where the Hamiltonian is obtained from Green's function theory and is written as:
The same DFT inputs used to generate the [http://media.yambo-code.eu/educational/tutorials/files/hBN-2D-RT.tar.gz hBN-2D-RT.tar.gz], are sufficient to converge the energy of the first exciton. You will need to increase the number of k-points to converge higher energy excitons.


[[File:H mb.png|600px|center|Many-Body Hamiltonian]]
==TD Hartree and TD DFT==
where <math>\rho_0</math> and <math>\gamma_0</math> are the density and the single-particle density matrix at equilibrium, <math>\Sigma^{COHSEX}</math> is the COHSEX self-energy and <math>V^H</math> is the Hartree potential. This Hamiltonian corresponds to a real-time version of the Bethe-Salpeter Equation<ref>[http://bcsbec.df.unicam.it/files/LaRNC11_N12%281988%29.pdf  G. Strinati, La Rivista del Nuovo Cimento '''11''' (12), 1-86 (1988)]</ref>. Then the polarization is calculated by means of Berry's phase formulation as it has been shown in the [[Real time approach to linear response (TDSE)]] tutorial.


==Prerequisites==
You need <code>yambo_nl</code> and <code> ypp_nl</code> compiled in double precision for this tutorial. The DFT inputs and yambo databases can be found here: [http://www.yambo-code.org/educational/tutorials/files/hBN10x10.tar.gz hBN10x10] .


==Real time Bethe-Salpeter Equation==
=== TD Hartree===
yambo_rt -n p -v hartree -F  Inputs_rt/02_td_hartree.in


This tutorial will show how to perform a simple real-time BSE calculation with Yambo on hBN monolayer. Use the same DFT inputs of the [http://www.yambo-code.org/educational/tutorials/files/hBN-2D.tar.gz previous tutorial], but increase the number of k-points to <code>10 10 1</code> in such a way to have converged exciton. Follow the first 6 steps of the [[Real time approach to linear response using TDSE|Real time approach to linear response using TDSE]]. Then generate the input file to calculate the collisions (see appendix of Ref. <ref name="prb88"></ref>) use the command : <code> yambo_nl -b -e -v h+sex</code>. The flag -b will tell the code to calculate the dielectric constant that is required for the screened interaction.
  negf                          # [R] Real-Time dynamics
  HXC_Potential= "HARTREE"      # [SC] SC HXC Potential
  HARRLvcs= 1000        mHa      # [HA] Hartree RL components
  VXCRLvcs= 0.          mHa      # [HA] DFT    RL components
  % RTBands
    3 | 5 |                    # [RT] Bands
  %
  Integrator= "RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
  PhLifeTime= 100.0000  fs      # [RT] Dephasing Time
  RTstep=10.000000      as      # [RT] Real Time step length
  NETime= 20.00000      fs      # [RT] Simulation Time
  % IOtime
  0.01    | 1.00    | 0.01    |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
  %
  % Field1_Freq
  0.00    | 0.00    | eV      # [RT Field1] Frequency
  %
  Field1_Int= 1.E3  kWLm2  # [RT Field1] Intensity
  Field1_Width= 0.000000 fs      # [RT Field1] Width
  Field1_kind= "DELTA"            # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
  Field1_pol= "linear"            # [RT Field1] Pol(linear|circular)
  % Field1_Dir
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor
  %
  % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
  %
  Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time
 
We set the cut-off on the Hartree potential to 1000 mHa. This defines the cutoff used to evaluate the Hartree potential at each time step.
Notice also the need of setting the cutoff to Vxc to zero.
This time we will propagate for just 20 fs. It is useful to run the simulation in background and then monitor the output file
 
  nohup yambo_rt -F Inputs_rt/02_td_hartree.in -J TD-HARTREE_1000mHa -C  TD-HARTREE_1000mHa &
  tail -f TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization
 
We can even have check the output on the fly.
To interrupt <code>tail -f </code>
  ctrl+C
Then
  gnuplot
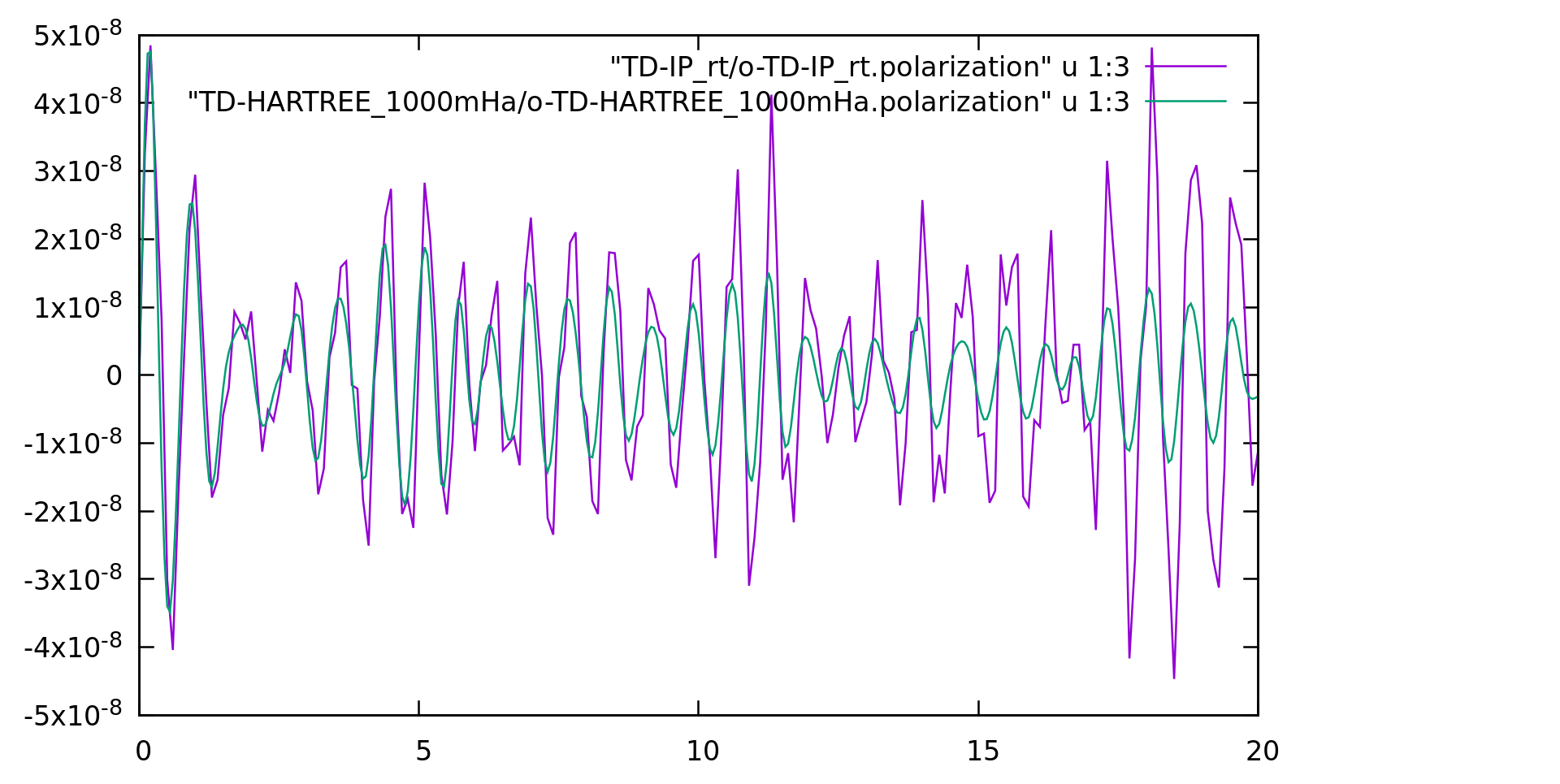
  plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l
  set xrange [0:20]
  rep "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization" u 1:3 w l
 
[[File:TD-Hartree Pol along y.png|thumb|center|900px|Time dependent polarization of hBN obtained within time depndent hartree]]
 
We can already see from the output that the polarization is not very different from the IP one.
The major difference is indeed due to the presence of a damping (or dephasing term) in the output (<code>PhLifeTime</code>, i.e. the life-time of the phase).
If we check the timing of the simulation we see that most of the time is spent in the following subroutines:
                        el_density_matrix :    7.5074 s CPU (    4002 calls,    0.0019 s avg)
                                V_Hartree :    1.0405 s CPU (    4002 calls,    0.0003 s avg)
                        V_real_space_to_H :  23.8210 s CPU (  220220 calls,    0.0001 s avg)
                          RT Hamiltonian :  32.5007 s CPU (    4001 calls,    0.0081 s avg)
The evaluation of the Hartree potential by itself does not take too much time. It is more consuming to evaluate the real space density.
However it is the projection of the potential into the transition space (V_real_space_to_H) which takes most of the time.
RT_Hamiltonian is just (roughly) the sum of the two previous subroutines. You can see how these timings change if you increase the cutoff on the Hartree potential.
 
 
Thus we can expect that also the absorption will be quite similar. Indeed hBN is uniform in the plane.
As previously you can now to a post-processing of the polarization. The input file is exactly the same
  ypp_rt -F  Inputs_rt/ypp_abs.in -J TD-HARTREE_1000mHa -C TD-HARTREE_1000mHa
  gnuplot
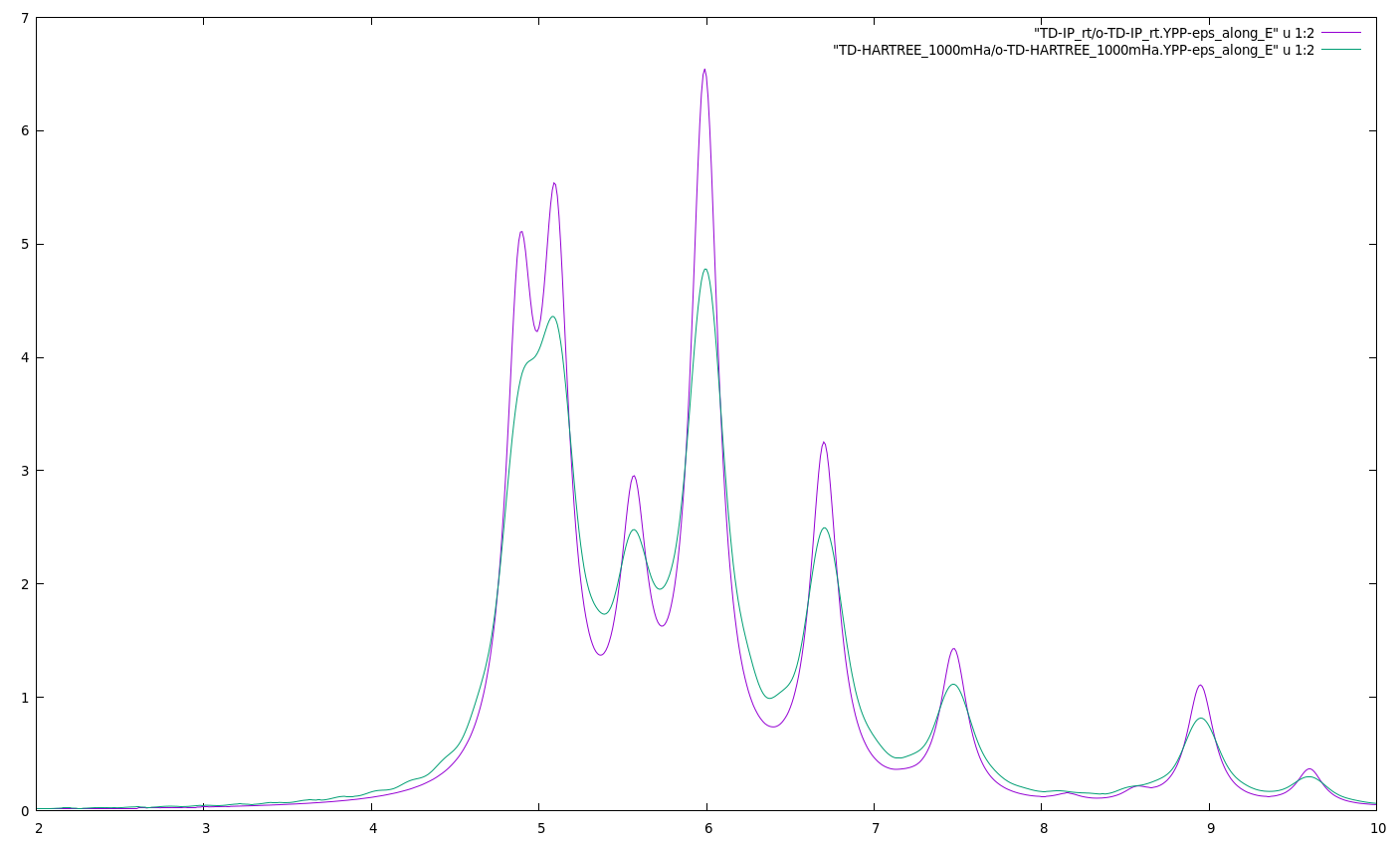
  plot "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l
  rep "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l
  set xrange [2:10]
  rep
 
[[File:Absorption along y.png|thumb|center|900px|hBN absorption within time dependent hartree]]
 
The situation would be completely different if we computed the polarization out of plane at both the TD-IP and the TD-Hartree level.
You can try if you wish, but remember that you have to go back to the original SAVE folder and remove the symmetries not consistent with a field along the z direction this time:
(see [[Prerequisites_for_Real_Time_propagation_with_Yambo|Prerequisites]]))
 
=== TD DFT===
You can now try to perform a TDDFT simulation.
Let's use the previous input file
  cp Inputs_rt/02_td_hartree.in Inputs_rt/03_td_dft.in
and modify it
  vim Input_rt/03_td_dft.in
 
  negf                            # [R] Real-Time dynamics
  HXC_Potential= "HARTREE+GS_XC"  # [SC] SC HXC Potential
  HARRLvcs= 1.E3      mHa        # [HA] Hartree    RL components
  VXCRLvcs= 1.E3      mHa
 
We can now run the TD-DFT simulation
  nohup yambo_rt -F Inputs_rt/03_td_dft.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA &
  tail -f TD-DFT_1000mHA/o-TD-DFT_1000mHA.polarization
 
and once it is over do the post processing
  ctrl+C
  ypp_rt_4.5_gpl -F Inputs_rt/ypp_abs.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA
  gnuplot
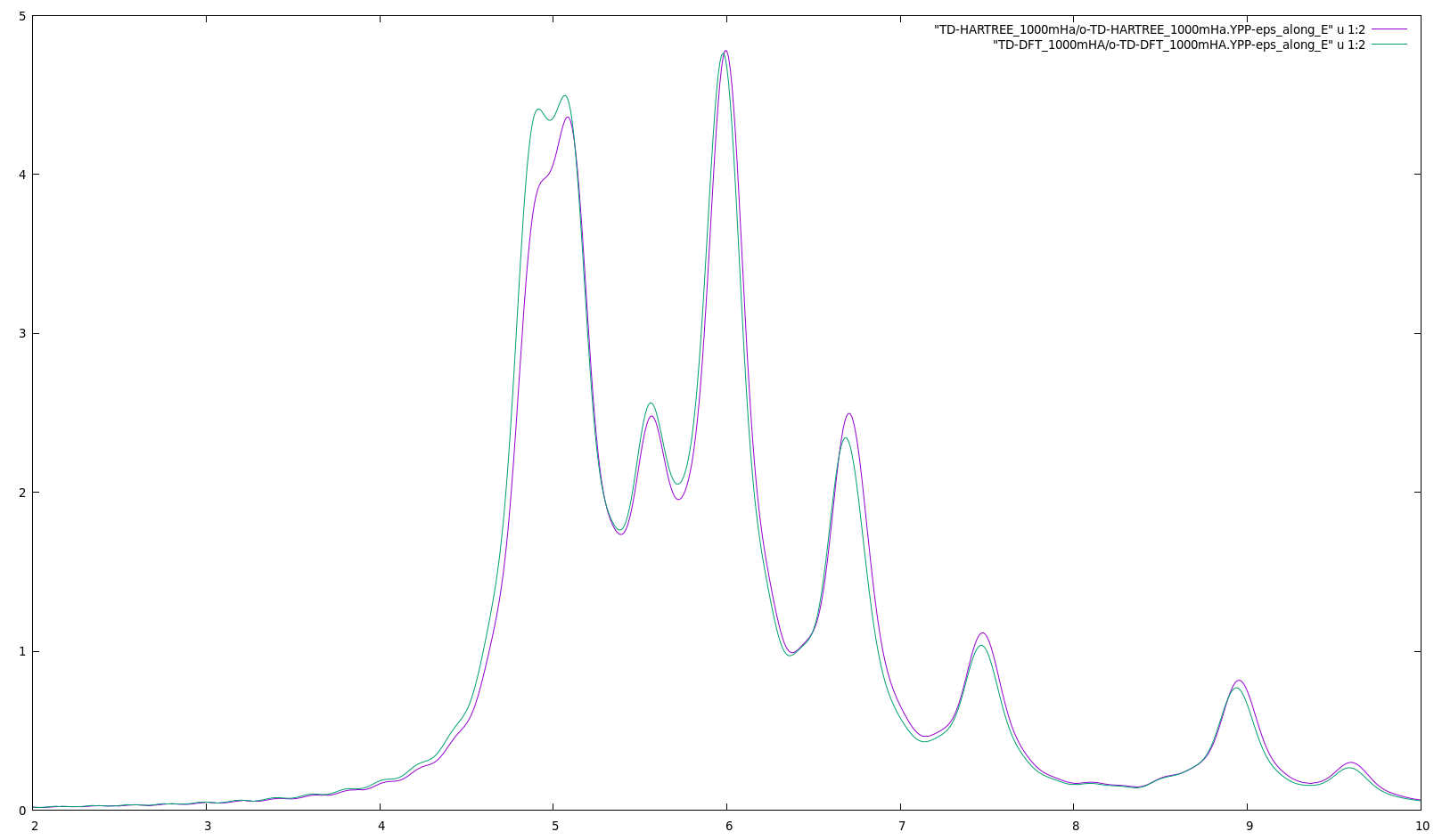
  gnuplot> plot "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l
  gnuplot> rep "TD-DFT_1000mHA/o-TD-DFT_1000mHA.YPP-eps_along_E" u 1:2 w l
 
[[File:Absorpion hBN TDDFT.png|center|900px|thumb|Absorption of hBN in plane. Comparison between TD-HARTREE and TDDFT]]
 
As expected TDDFT does not improve much over TD-HARTREE in extended systems
 
==The Real Time Collisions==
 
We next move to the evaluation of the collisions. (see [[Introduction to Real Time propagation in Yambo]] to remember what are the collisions)
This part is common in between the <code>yambo_nl</code> and the <code>yambo_rt</code>.
 
Then generate the input file to calculate the collisions (see appendix of Ref. <ref name="prb88">[https://arxiv.org/abs/1109.2424 C. Attaccalite, M. Grüning, and A. Marini PRB '''84''', 245110 (2011)]</ref>) use the command :
  yambo_rt -X s -e -v hsex -F Inputs/03_coll_hsex.in
 
The flag -b will tell the code to calculate the dielectric constant that is required for the screened interaction.
It could be even computed in an independent calculation and then loaded using the <code>-J</code> flags


  em1s                          # [R Xs] Static Inverse Dielectric Matrix
  em1s                          # [R Xs] Static Inverse Dielectric Matrix
collisions                    # [R] Eval the extended Collisions
  dipoles                        # [R  ] Compute the dipoles
  dipoles                        # [R  ] Compute the dipoles
DIP_Threads=0                  # [OPENMP/X] Number of threads for dipoles
X_Threads=0                    # [OPENMP/X] Number of threads for response functions
RT_Threads=0                  # [OPENMP/RT] Number of threads for real-time
  Chimod= "HARTREE"              # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  Chimod= "HARTREE"              # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  % BndsRnXs
  % BndsRnXs
     1 |  40 |                  # [Xs] Polarization function bands
     1 |  20 |                  # [Xs] Polarization function bands
  %
  %
  NGsBlkXs= <span style="color:red">1000</span> mHa      # [Xs] Response block size
  NGsBlkXs= <span style="color:red">1000</span> mHa      # [Xs] Response block size
Line 33: Line 136:
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
   1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
  %
  %
While this is the part of the input file specific for the evaluation of the collisions
collisions                    # [R] Eval the extended Collisions
  % [[Variables#COLLBands|COLLBands]]
  % [[Variables#COLLBands|COLLBands]]
   <span style="color:red">4 | 5 | </span>                 # [COLL] Bands for the collisions
   <span style="color:red">4 </span>| <span style="color:red"> 5  </span>|                  # [COLL] Bands for the collisions
  %
  %
  HXC_Potential= "HARTREE+SEX"          # [SC] SC HXC Potential
  HXC_Potential= "HARTREE+SEX"          # [SC] SC HXC Potential
Line 42: Line 148:
   
   


With this input, we calculate the HARTREE and SEX collisions integrals. Notice that the HARTREE term in principle can be calculated on the fly, but in this way it is more efficient especially for the non-linear response.  
With this input, we calculate the HARTREE plus SEX collisions integrals. Notice that the HARTREE term in principle can be calculated on the fly, but in this way it is more efficient especially for the non-linear response.  
Here one has to converge the cutoff for the Hartree and the Screened Exchange, usually, around <code>5000 mHa</code> it is a good value, in this example, I put <code>1000 mHa</code> to speed up calculations. The collisions bands <code>COLLBands</code> have to be the same number of bands you want to use in the linear/nonlinear response. Run this calculation, it will take 5 minutes on a serial PC.
Here one has to converge the cutoff for the Hartree and the Screened Exchange. Around <code>5000 mHa</code> is a reasonable value for hBN. In this example we will use <code>1000 mHa</code> to speed up calculations. The collisions bands <code>COLLBands</code> have to be the same number of bands you want to use in the linear/nonlinear response.
The you can run
  yambo_rt -F Inputs/03_coll_hsex.in -J COLL_HSEX -C COLL_HSEX


Then you generate the input for the linear response <code>yambo_nl -u -V qp</code> :
The calculation will take about 1 minute in serial.
It produced many binary files <code>ndb.COLLISIONS_HXC_fragment_*</code> which will be needed to perform TD-HSEX simulations.
Notice that, if you want, you can also compute simple HARTREE collisions and use them in a TD-HARTREE simulation.


=== TD-HARTREE with collisions (facultative) ===
Then generate the input file to calculate the collisions (see appendix of Ref. <ref name="prb88"></ref>) use the command :
  yambo_rt -e -v h -F Inputs/03_coll_hartree.in
with a simpler input file
collisions                    # [R] Eval the extended Collisions
% [[Variables#COLLBands|COLLBands]]
  <span style="color:red">4  </span> | <span style="color:red"> 5  </span> |                # [COLL] Bands for the collisions
%
HXC_Potential= "HARTREE"          # [SC] SC HXC Potential
[[Variables#HARRLvcs|HARRLvcs]]= <span style="color:red">1000 </span>mHa      # [HA] Hartree    RL components
  yambo_rt -F Inputs/03_coll_hartree.in -J COLL_HARTREE -C COLL_HARTREE
  yambo_rt -F Inputs_rt/02_td_hartree.in -J "TD-HARTREE_COLL,COLL_HARTREE" -C TD-HARTREE_COLL
and compare the run with the simulation without collision.
One major difference, is that, when the collisions are used, yambo does not need to load the wave--function anymore and the simulation is much faster.
The drawback is that for big systems the folder COLL_HARTREE may become huge, thus requiring a lot of disk space.
==Time dependent Bethe Salpeter equation==
=== Approach based on the density matrix ===
To generate the input for the real-time simulation you can run
yambo_rt -n p -v hsex -V qp -F Inputs_rt/04_td_hsex.in
As you can see this time the extra verbosity for quasi-particles is used <code>-V qp</code>
The reason is that, to be consistent with the TD-HSEX, simulation we need to apply quasi-particles corrections.
The input file is
  negf                          # [R] NEQ Real-time dynamics
  HXC_Potential= "SEX+HARTREE"  # [SC] SC HXC Potential
  % RTBands
    3 | 5 |                    # [RT] Bands
  %
  Integrator= "RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
  PhLifeTime= 100.0000  fs      # [RT] Dephasing Time
  RTstep=10.000000      as      # [RT] Real Time step length
  NETime= 30.00000      fs      # [RT] Simulation Time
  % IOtime
  0.01    | 1.00    | 0.05    |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
  %
  HARRLvcs= 1000      mHa      # [HA] Hartree    RL components
  EXXRLvcs= 1000      mHa      # [XX] Exchange    RL components
  CORRLvcs= 1000      mHa      # [GW] Correlation RL components
% GfnQP_E
  <span style="color:red">3.000000 </span>| 1.000000 | 1.000000 |      # [EXTQP G] E parameters  (c/v) eV|adim|adim
%
  % Field1_Freq
  0.00    | 0.00    | eV      # [RT Field1] Frequency
  %
  Field1_Int= 1.E3  kWLm2  # [RT Field1] Intensity
  Field1_Width= 0.000000 fs      # [RT Field1] Width
  Field1_kind= "DELTA"            # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
  Field1_pol= "linear"            # [RT Field1] Pol(linear|circular)
  % Field1_Dir
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor
  %
  % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
  %
  Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time
and then run the code. Notice the presence of the <code>COLL_SEX</code> among the options after <code>-J</code>
nohup yambo_rt -F Inputs_rt/04_td_hsex.in -J "TD-SEX_rt,COLL_SEX" -C TD-SEX_rt
=== Approach based on the Berry Phase ===
To generate the input for the real-time simulation you can run
yambo_nl -u -V qp -F Inputs_nl/04_td-sex.in
The input file is


  nloptics                      # [R NL] Non-linear optics
  nloptics                      # [R NL] Non-linear optics
Line 56: Line 242:
  NLverbosity= "low"            # [NL] Verbosity level (low | high)
  NLverbosity= "low"            # [NL] Verbosity level (low | high)
  NLstep=  0.0100      fs      # [NL] Real Time step length
  NLstep=  0.0100      fs      # [NL] Real Time step length
  NLtime= <span style="color:red">55.00000</span>      fs      # [NL] Simulation Time
  NLtime= <span style="color:red">20.00000</span>      fs      # [NL] Simulation Time
  NLintegrator= "<span style="color:red">CRANKNIC</span>"        # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
  NLintegrator= "<span style="color:red">CRANKNIC</span>"        # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
  NLCorrelation= "<span style="color:red">SEX</span>"          # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX")
  NLCorrelation= "<span style="color:red">SEX</span>"          # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX")
Line 68: Line 254:
  #FrSndOrd                      # [NL] Force second order in Covariant Dipoles
  #FrSndOrd                      # [NL] Force second order in Covariant Dipoles
  #EvalCurrent                  # [NL] Evaluate the current
  #EvalCurrent                  # [NL] Evaluate the current
  HARRLvcs= 1017         RL      # [HA] Hartree    RL components
  HARRLvcs= 1000         mHa    # [HA] Hartree    RL components
  EXXRLvcs= 1074         mHa    # [XX] Exchange    RL components
  EXXRLvcs= 1000         mHa    # [XX] Exchange    RL components
  % ExtF_Dir
  % ExtF_Dir
   <span style="color:red">0.000000 | 1.000000 | 0.000000 | </span>      # [NL ExtF] Versor
   <span style="color:red">0.000000 | 1.000000 | 0.000000 | </span>      # [NL ExtF] Versor
Line 78: Line 264:
  ExtF_Tstart=  0.0100  fs      # [NL ExtF] Initial Time
  ExtF_Tstart=  0.0100  fs      # [NL ExtF] Initial Time
  % GfnQP_E
  % GfnQP_E
   <span style="color:red">3.000000 | 1.000000 | 1.000000 | </span>      # [EXTQP G] E parameters  (c/v) eV|adim|adim
   <span style="color:red">3.000000 </span>| 1.000000 | 1.000000 |       # [EXTQP G] E parameters  (c/v) eV|adim|adim
  %
  %


Notice that we introduced a scissor operator (a rigid shift of the conduction bands) of 3.0 eV. In principle, it is possible to perform a G<sub>0</sub>W<sub>0</sub> calculation with Yambo and use the Quasi-particle band structure instead of the rigid shift. Run this calculation and then analyze the result in the same way of linear response tutorial, you will get a nice exciton in hBN, as the one plotted below in the old tutorial. You can repeat the same kind of calculations for the non-linear response.
Notice that we introduced a scissor operator (a rigid shift of the conduction bands) of 3.0 eV. In principle, it is possible to perform a G<sub>0</sub>W<sub>0</sub> calculation with Yambo and use the Quasi-particle band structure instead of the rigid shift. Run this calculation and then analyze the result in the same way of linear response tutorial, you will get a nice exciton in hBN, as the one plotted below in the old tutorial. You can repeat the same kind of calculations for the non-linear response.
Notice that in the calculation we decreased the number of G-vectors in the Hartree term,  [[Variables#HARRLvcs|HARRLvcs]]  to speed up the calculation, in case of BN this does not change the result because local field effects are very small in h-BN along the plane.
Notice that in the calculation we decreased the number of G-vectors in the Hartree term,  [[Variables#HARRLvcs|HARRLvcs]]  to speed up the calculation, in case of BN this does not change the result because local field effects are very small in h-BN along the plane.
Now you can analyze the response with <code>ypp</code> as it was done the linear response tutorial and compare with the standard Bethe-Salpeter (input [[tutorials/lumen.in_bse|here]]):


[[File:RT BSE.png|600px|center|Dielectric constant with excitons]]
nohup yambo_nl -F Inputs_nl/04_td_hsex.in -J "TD-SEX_nl,COLL_SEX" -C TD-SEX_nl
 
=== Final post processing ===
 
Now you can analyze the response with
ypp_rt -F Inputs_rt/ypp_abs.in -J TD-sex_rt -C TD-SEX_rt
ypp_nl -F Inputs_nl/ypp_abs.in -J TD-SEX_nl -C TD-SEX_nl
as it was done the linear response tutorial and compare with the TD-IP run (and eventually against the standard Bethe-Salpeter):
 
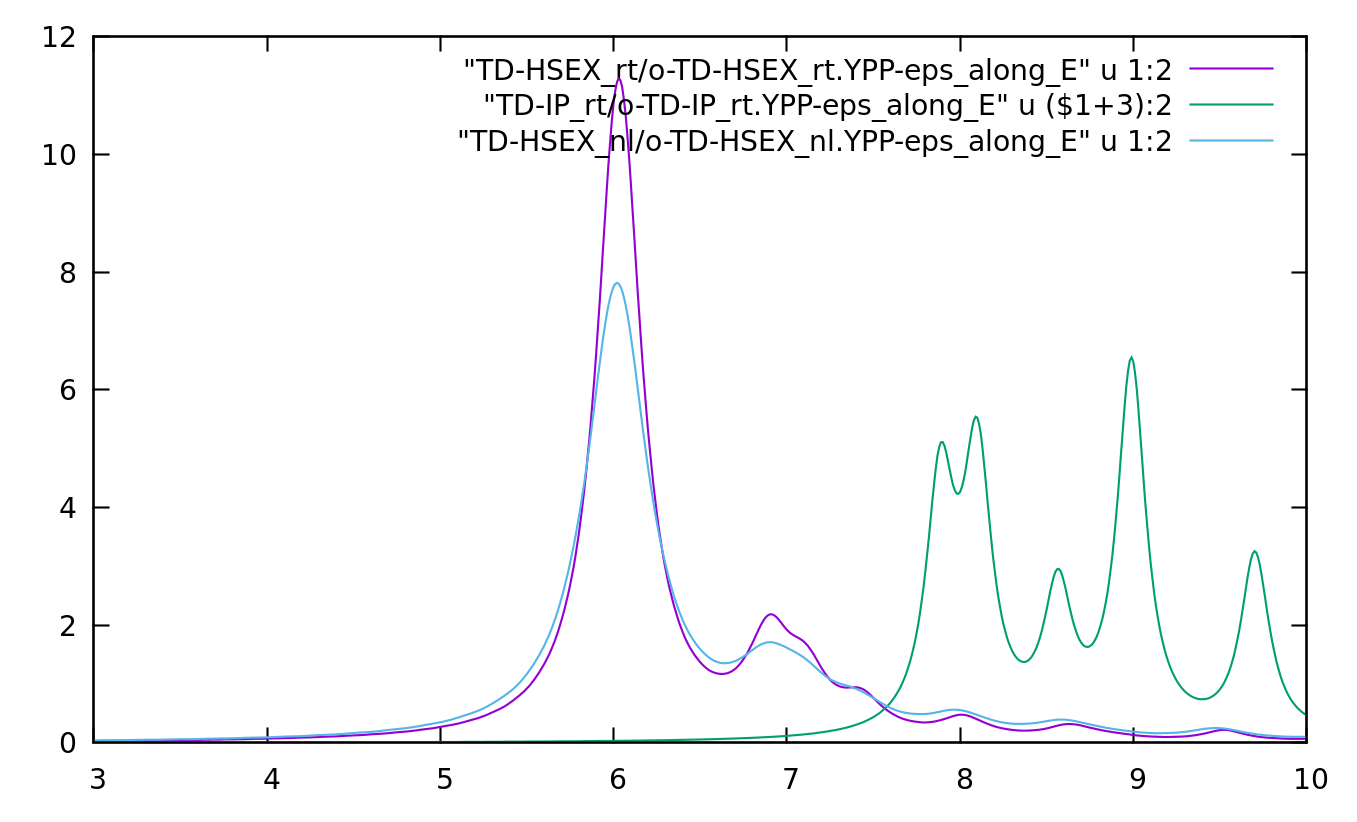
gnuplot> plot "TD-HSEX_rt/o-TD-HSEX_rt.YPP-eps_along_E" u 1:2 w l
gnuplot> rep "TD-HSEX_nl/o-TD-HSEX_nl.YPP-eps_along_E" u 1:2 w l
gnuplot> set xrange [3:10]
gnuplot> set yrange [0:12]
gnuplot> rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u ($1+3):2 w l
 
[[File:HBN HSEX absorption.png|thumb|900px|center|In plane absorption of hBN at the TD-HSEX level compared with IP absorption]]


Linear response results can be obtained following the [[How to obtain an optical spectrum|BSE tutorial]].  
Linear response results can be obtained following the [[How to obtain an optical spectrum|BSE tutorial]].  
Notice that you can use the SEX approximation for the non-linear response too (see the following tutorials on non-linear response).
Notice that you can use the SEX approximation for the non-linear response too (see the following tutorials on non-linear response).
==References==
==References==
<references />
<references />
<br>
{| style="width:100%" border="1"
|style="width:15%; text-align:left"|Prev: [[Real time approach to linear response|Independent Particles ]]
|style="width:70%; text-align:center"|Now: [[Tutorials|Tutorials]] --> [[Linear response from real time simulations|Linear Response]] -->  [[Real time Bethe-Salpeter Equation (TDSE)]]
|style="width:35%; text-align:right"|Next: If you did all steps you can go back to the previous level
|-
|}

Latest revision as of 17:31, 11 September 2023

Introduction

This tutorial will show how to perform a real-time calculation with Yambo on hBN monolayer. We will go through different approximations for the many body self--energy (HXC potential in the yambo language) up to the HSEX approximation which captures the physics of the exciton. For approximations local in space, like "TD-HARTREE" and "TD-DFT", the HXC potential can be evaluated directly during the simulation from real space quantities. On the contrary for approximations non local in space, one first need to compute the "real time collisions".

The same DFT inputs used to generate the hBN-2D-RT.tar.gz, are sufficient to converge the energy of the first exciton. You will need to increase the number of k-points to converge higher energy excitons.

TD Hartree and TD DFT

TD Hartree

yambo_rt -n p -v hartree -F  Inputs_rt/02_td_hartree.in

 negf                           # [R] Real-Time dynamics
 HXC_Potential= "HARTREE"       # [SC] SC HXC Potential
 HARRLvcs= 1000        mHa      # [HA] Hartree RL components
 VXCRLvcs= 0.          mHa      # [HA] DFT     RL components
 % RTBands
   3 | 5 |                     # [RT] Bands
 %
 Integrator= "RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
 PhLifeTime= 100.0000   fs      # [RT] Dephasing Time
 RTstep=10.000000       as      # [RT] Real Time step length
 NETime= 20.00000       fs      # [RT] Simulation Time
 % IOtime
  0.01     | 1.00     | 0.01     |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
 %
 % Field1_Freq
  0.00     | 0.00     | eV      # [RT Field1] Frequency
 %
 Field1_Int= 1.E3   kWLm2   # [RT Field1] Intensity
 Field1_Width= 0.000000 fs      # [RT Field1] Width
 Field1_kind= "DELTA"            # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
 Field1_pol= "linear"             # [RT Field1] Pol(linear|circular)
 % Field1_Dir
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor
 %
 % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
 %
 Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time

We set the cut-off on the Hartree potential to 1000 mHa. This defines the cutoff used to evaluate the Hartree potential at each time step. Notice also the need of setting the cutoff to Vxc to zero. This time we will propagate for just 20 fs. It is useful to run the simulation in background and then monitor the output file 

 nohup yambo_rt -F Inputs_rt/02_td_hartree.in -J TD-HARTREE_1000mHa -C  TD-HARTREE_1000mHa &
 tail -f TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization

We can even have check the output on the fly. To interrupt tail -f 

 ctrl+C

Then 

 gnuplot
 plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l
 set xrange [0:20]
 rep "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.polarization" u 1:3 w l
Time dependent polarization of hBN obtained within time depndent hartree

We can already see from the output that the polarization is not very different from the IP one. The major difference is indeed due to the presence of a damping (or dephasing term) in the output (PhLifeTime, i.e. the life-time of the phase). If we check the timing of the simulation we see that most of the time is spent in the following subroutines: 

                       el_density_matrix :    7.5074 s CPU (    4002 calls,    0.0019 s avg)
                               V_Hartree :    1.0405 s CPU (    4002 calls,    0.0003 s avg)
                       V_real_space_to_H :   23.8210 s CPU (  220220 calls,    0.0001 s avg)
                          RT Hamiltonian :   32.5007 s CPU (    4001 calls,    0.0081 s avg)

The evaluation of the Hartree potential by itself does not take too much time. It is more consuming to evaluate the real space density. However it is the projection of the potential into the transition space (V_real_space_to_H) which takes most of the time. RT_Hamiltonian is just (roughly) the sum of the two previous subroutines. You can see how these timings change if you increase the cutoff on the Hartree potential.


Thus we can expect that also the absorption will be quite similar. Indeed hBN is uniform in the plane. As previously you can now to a post-processing of the polarization. The input file is exactly the same 

 ypp_rt -F  Inputs_rt/ypp_abs.in -J TD-HARTREE_1000mHa -C TD-HARTREE_1000mHa
 gnuplot
 plot "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l
 rep "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l
 set xrange [2:10]
 rep
hBN absorption within time dependent hartree

The situation would be completely different if we computed the polarization out of plane at both the TD-IP and the TD-Hartree level. You can try if you wish, but remember that you have to go back to the original SAVE folder and remove the symmetries not consistent with a field along the z direction this time: (see Prerequisites))

TD DFT

You can now try to perform a TDDFT simulation. Let's use the previous input file 

 cp Inputs_rt/02_td_hartree.in Inputs_rt/03_td_dft.in

and modify it 

 vim Input_rt/03_td_dft.in

 negf                            # [R] Real-Time dynamics
 HXC_Potential= "HARTREE+GS_XC"  # [SC] SC HXC Potential
 HARRLvcs= 1.E3       mHa        # [HA] Hartree     RL components
 VXCRLvcs= 1.E3       mHa

We can now run the TD-DFT simulation 

 nohup yambo_rt -F Inputs_rt/03_td_dft.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA &
 tail -f TD-DFT_1000mHA/o-TD-DFT_1000mHA.polarization

and once it is over do the post processing 

 ctrl+C
 ypp_rt_4.5_gpl -F Inputs_rt/ypp_abs.in -J TD-DFT_1000mHA -C TD-DFT_1000mHA
 gnuplot
 gnuplot> plot "TD-HARTREE_1000mHa/o-TD-HARTREE_1000mHa.YPP-eps_along_E" u 1:2 w l
 gnuplot> rep "TD-DFT_1000mHA/o-TD-DFT_1000mHA.YPP-eps_along_E" u 1:2 w l
Absorption of hBN in plane. Comparison between TD-HARTREE and TDDFT

As expected TDDFT does not improve much over TD-HARTREE in extended systems

The Real Time Collisions

We next move to the evaluation of the collisions. (see Introduction to Real Time propagation in Yambo to remember what are the collisions) This part is common in between the yambo_nl and the yambo_rt.

Then generate the input file to calculate the collisions (see appendix of Ref. [1]) use the command : 

 yambo_rt -X s -e -v hsex -F Inputs/03_coll_hsex.in

The flag -b will tell the code to calculate the dielectric constant that is required for the screened interaction. It could be even computed in an independent calculation and then loaded using the -J flags 

em1s                           # [R Xs] Static Inverse Dielectric Matrix
dipoles                        # [R   ] Compute the dipoles
Chimod= "HARTREE"              # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
% BndsRnXs
   1 |  20 |                   # [Xs] Polarization function bands
%
NGsBlkXs= 1000 mHa      # [Xs] Response block size
% DmRngeXs
  0.10000 |  0.10000 | eV      # [Xs] Damping range
%
% LongDrXs
 1.000000 | 0.000000 | 0.000000 |        # [Xs] [cc] Electric Field
%

While this is the part of the input file specific for the evaluation of the collisions 

collisions                     # [R] Eval the extended Collisions
% COLLBands
  4 |  5  |                  # [COLL] Bands for the collisions
%
HXC_Potential= "HARTREE+SEX"           # [SC] SC HXC Potential
HARRLvcs= 1000 mHa      # [HA] Hartree     RL components
EXXRLvcs= 1000 mHa      # [XX] Exchange    RL components
CORRLvcs= 1000 mHa      # [GW] Correlation RL components

With this input, we calculate the HARTREE plus SEX collisions integrals. Notice that the HARTREE term in principle can be calculated on the fly, but in this way it is more efficient especially for the non-linear response. Here one has to converge the cutoff for the Hartree and the Screened Exchange. Around 5000 mHa is a reasonable value for hBN. In this example we will use 1000 mHa to speed up calculations. The collisions bands COLLBands have to be the same number of bands you want to use in the linear/nonlinear response. The you can run 

 yambo_rt -F Inputs/03_coll_hsex.in -J COLL_HSEX -C COLL_HSEX

The calculation will take about 1 minute in serial. It produced many binary files ndb.COLLISIONS_HXC_fragment_* which will be needed to perform TD-HSEX simulations. Notice that, if you want, you can also compute simple HARTREE collisions and use them in a TD-HARTREE simulation.

TD-HARTREE with collisions (facultative)

Then generate the input file to calculate the collisions (see appendix of Ref. [1]) use the command : 

 yambo_rt -e -v h -F Inputs/03_coll_hartree.in

with a simpler input file 

collisions                     # [R] Eval the extended Collisions
% COLLBands
  4   |  5    |                 # [COLL] Bands for the collisions
%
HXC_Potential= "HARTREE"           # [SC] SC HXC Potential
HARRLvcs= 1000 mHa      # [HA] Hartree     RL components

 yambo_rt -F Inputs/03_coll_hartree.in -J COLL_HARTREE -C COLL_HARTREE
 yambo_rt -F Inputs_rt/02_td_hartree.in -J "TD-HARTREE_COLL,COLL_HARTREE" -C TD-HARTREE_COLL

and compare the run with the simulation without collision. One major difference, is that, when the collisions are used, yambo does not need to load the wave--function anymore and the simulation is much faster. The drawback is that for big systems the folder COLL_HARTREE may become huge, thus requiring a lot of disk space.

Time dependent Bethe Salpeter equation

Approach based on the density matrix

To generate the input for the real-time simulation you can run 

yambo_rt -n p -v hsex -V qp -F Inputs_rt/04_td_hsex.in

As you can see this time the extra verbosity for quasi-particles is used -V qp The reason is that, to be consistent with the TD-HSEX, simulation we need to apply quasi-particles corrections. The input file is 

 negf                           # [R] NEQ Real-time dynamics
 HXC_Potential= "SEX+HARTREE"   # [SC] SC HXC Potential
 % RTBands
   3 | 5 |                     # [RT] Bands
 %
 Integrator= "RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
 PhLifeTime= 100.0000   fs      # [RT] Dephasing Time
 RTstep=10.000000       as      # [RT] Real Time step length
 NETime= 30.00000       fs      # [RT] Simulation Time
 % IOtime
  0.01     | 1.00     | 0.05     |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
 %
 HARRLvcs= 1000       mHa      # [HA] Hartree     RL components
 EXXRLvcs= 1000       mHa      # [XX] Exchange    RL components
 CORRLvcs= 1000       mHa      # [GW] Correlation RL components

% GfnQP_E
 3.000000 | 1.000000 | 1.000000 |       # [EXTQP G] E parameters  (c/v) eV|adim|adim
%

 % Field1_Freq
  0.00     | 0.00     | eV      # [RT Field1] Frequency
 %
 Field1_Int= 1.E3   kWLm2   # [RT Field1] Intensity
 Field1_Width= 0.000000 fs      # [RT Field1] Width
 Field1_kind= "DELTA"            # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
 Field1_pol= "linear"             # [RT Field1] Pol(linear|circular)
 % Field1_Dir
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor
 %
 % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
 %
 Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time

and then run the code. Notice the presence of the COLL_SEX among the options after -J 

nohup yambo_rt -F Inputs_rt/04_td_hsex.in -J "TD-SEX_rt,COLL_SEX" -C TD-SEX_rt


Approach based on the Berry Phase

To generate the input for the real-time simulation you can run 

yambo_nl -u -V qp -F Inputs_nl/04_td-sex.in

The input file is 

nloptics                       # [R NL] Non-linear optics
DIP_Threads=0                  # [OPENMP/X] Number of threads for dipoles
NL_Threads=0                   # [OPENMP/NL] Number of threads for nl-optics
% NLBands
  4 |  5 |                     # [NL] Bands
%
NLverbosity= "low"             # [NL] Verbosity level (low | high)
NLstep=   0.0100       fs      # [NL] Real Time step length
NLtime= 20.00000       fs      # [NL] Simulation Time
NLintegrator= "CRANKNIC"         # [NL] Integrator ("EULEREXP/RK2/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "SEX"           # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/LRW/JGM/SEX")
NLLrcAlpha= 0.000000           # [NL] Long Range Correction
% NLEnRange
 0.200000 | 8.000000 | eV      # [NL] Energy range
%
NLEnSteps= 1                   # [NL] Energy steps
NLDamping=  0.10000    eV      # [NL] Damping
#UseDipoles                    # [NL] Use Covariant Dipoles (just for test purpose)
#FrSndOrd                      # [NL] Force second order in Covariant Dipoles
#EvalCurrent                   # [NL] Evaluate the current
HARRLvcs= 1000         mHa     # [HA] Hartree     RL components
EXXRLvcs= 1000         mHa     # [XX] Exchange    RL components
% ExtF_Dir
 0.000000 | 1.000000 | 0.000000 |        # [NL ExtF] Versor
%
ExtF_Int= 1000.        kWLm2   # [NL ExtF] Intensity
ExtF_Width= 0.000000   fs      # [NL ExtF] Field Width
ExtF_kind= "DELTA"             # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
ExtF_Tstart=   0.0100  fs      # [NL ExtF] Initial Time
% GfnQP_E
 3.000000 | 1.000000 | 1.000000 |        # [EXTQP G] E parameters  (c/v) eV|adim|adim
%

Notice that we introduced a scissor operator (a rigid shift of the conduction bands) of 3.0 eV. In principle, it is possible to perform a G0W0 calculation with Yambo and use the Quasi-particle band structure instead of the rigid shift. Run this calculation and then analyze the result in the same way of linear response tutorial, you will get a nice exciton in hBN, as the one plotted below in the old tutorial. You can repeat the same kind of calculations for the non-linear response. Notice that in the calculation we decreased the number of G-vectors in the Hartree term, HARRLvcs to speed up the calculation, in case of BN this does not change the result because local field effects are very small in h-BN along the plane. 

nohup yambo_nl -F Inputs_nl/04_td_hsex.in -J "TD-SEX_nl,COLL_SEX" -C TD-SEX_nl

Final post processing

Now you can analyze the response with 

ypp_rt -F Inputs_rt/ypp_abs.in -J TD-sex_rt -C TD-SEX_rt
ypp_nl -F Inputs_nl/ypp_abs.in -J TD-SEX_nl -C TD-SEX_nl

as it was done the linear response tutorial and compare with the TD-IP run (and eventually against the standard Bethe-Salpeter): 

gnuplot> plot "TD-HSEX_rt/o-TD-HSEX_rt.YPP-eps_along_E" u 1:2 w l
gnuplot> rep "TD-HSEX_nl/o-TD-HSEX_nl.YPP-eps_along_E" u 1:2 w l
gnuplot> set xrange [3:10]
gnuplot> set yrange [0:12]
gnuplot> rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u ($1+3):2 w l
In plane absorption of hBN at the TD-HSEX level compared with IP absorption

Linear response results can be obtained following the BSE tutorial. Notice that you can use the SEX approximation for the non-linear response too (see the following tutorials on non-linear response).

References

  1. ↑ 1.0 1.1 C. Attaccalite, M. Grüning, and A. Marini PRB 84, 245110 (2011)


Prev: Independent Particles Now: Tutorials --> Linear Response --> Real time Bethe-Salpeter Equation (TDSE) Next: If you did all steps you can go back to the previous level
Retrieved from "https://wiki.yambo-code.eu/wiki/index.php?title=Real_time_Bethe-Salpeter_Equation_(TDSE)&oldid=7165"