Real time approach to linear response: Difference between revisions

From The Yambo Project
Jump to navigation Jump to search
No edit summary
m (Typo fixes)
 
(51 intermediate revisions by 3 users not shown)
Line 1: Line 1:
==Background==
== Introduction ==


The Yambo code implements a real-time effective Schrödinger equation, where the coupling between electrons and the external field is described by means of the [http://www.theochem.unito.it/didattica/tec-comp_sdm/note1.pdf Modern Theory of Polarization]:
In this example, we will consider a single layer of hexagonal boron nitride (hBN).
If you didn't before you can download input files and Yambo databases for this tutorial here: [https://media.yambo-code.eu/educational/tutorials/files/hBN-2D-RT.tar.gz hBN-2D-RT.tar.gz].
and/or follow the instructions to generate the databases here: [[Prerequisites for Real Time propagation with Yambo]]


Before proceeding with the real-time simulations it is useful to compute the Independent Particles (IP) absorption spectrum of hBN along the y direction.
If you didn't before create an Inputs folder and then the input file with the commands
mkdir Inputs
yambo_nl -o c -F Inputs/01_ip.in
and set the proper input parameters
  optics                        # [R OPT] Optics
  chi                            # [R CHI] Dyson equation for Chi.
  dipoles                        # [R  ] Compute the dipoles
  Chimod= "IP"                  # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
  % QpntsRXd
    1 |  1 |                  # [Xd] Transferred momenta
  %
  % BndsRnXd
    3 | 6 |                    # [Xd] Polarization function bands
  %
  % EnRngeXd
    0.00000 | 20.00000 | eV      # [Xd] Energy range
  %
  % DmRngeXd
    0.10000 |  0.10000 | eV      # [Xd] Damping range
  %
  ETStpsXd= 2001                  # [Xd] Total Energy steps
  % LongDrXd
  0.000000 | 1.000000 | 0.000000 |        # [Xd] [cc] Electric Field
  %
and then run the code
yambo_nl -F Inputs/01_ip.in -J CHI_IP -C CHI_IP


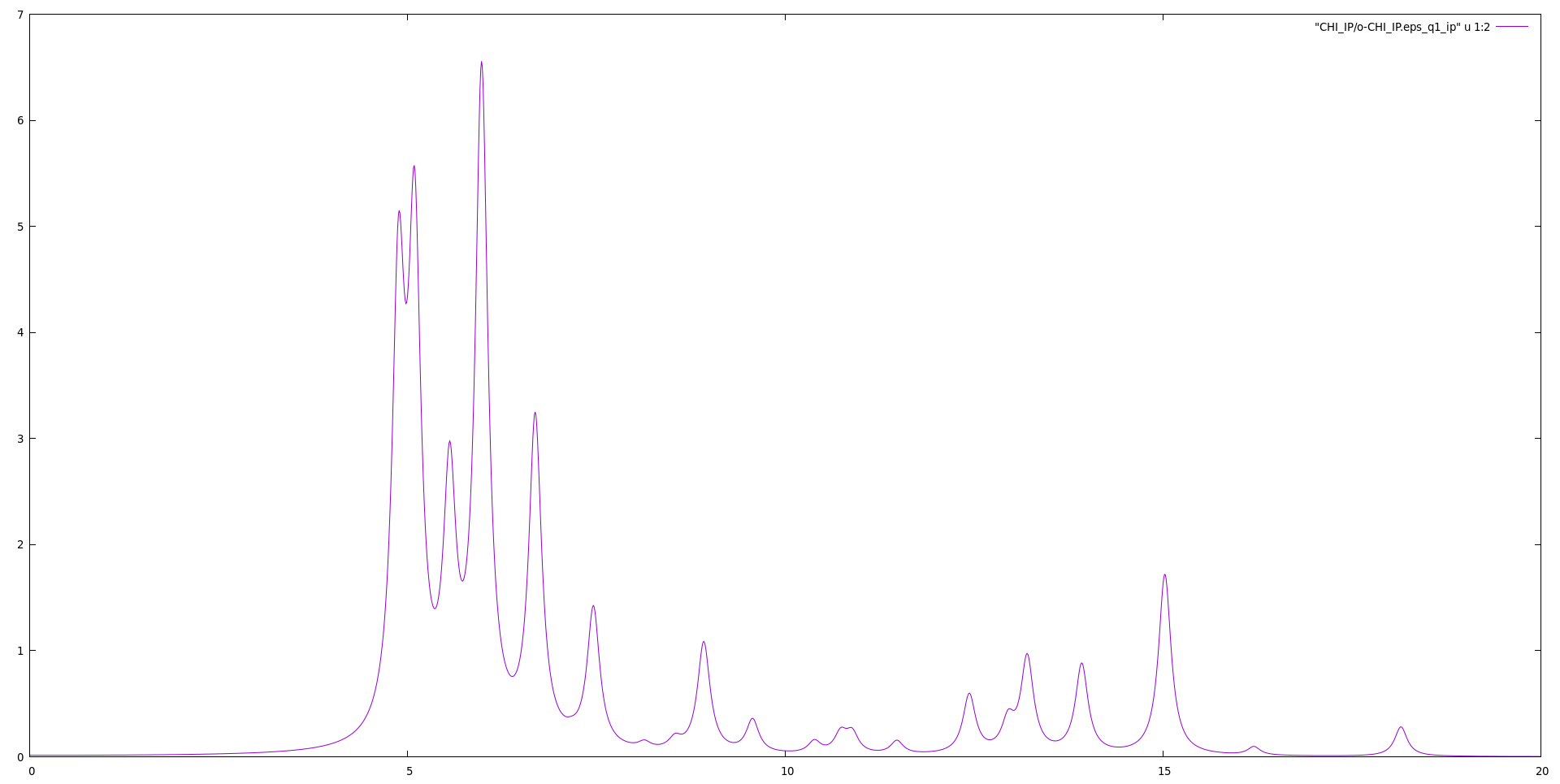
<math> i \hbar \frac{\partial}{\partial t} | v_{i \mathbf{k}} \rangle = \left( \hat H^{sys}_{\mathbf k} + i e \mathcal{E}(t) \cdot \partial_{\mathbf k} \right ) | v_{i \mathbf{k}} \rangle</math>
The resulting spectrum will give an idea of the energy involved in the real-time simulations
gnuplot
gnuplot> plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l
[[File:Independent Particles absorption for hBN.png|thumb|center|900px|Independent Particles absorptions for hBN comuting using 4 bands and with LDA eigenvalues]]


==Real-time dynamics at the independent particles level ==


Where  <math> | v_{i \mathbf{k}} \rangle </math> are the time-dependent valence bands, Hsysk is the Hamiltonian, <math>E(t)</math> is the external field and the term <math> i e \partial k</math> corresponds to the dipole operator in periodic systems. For more details on this last term see [https://cfm.ehu.es/ivo/publications/souza_prb04.pdf PRB 69, 085106 (2004)] and [https://arxiv.org/abs/1309.4012v2 Rev. B, 88, 235113 (2013)].
Since we work with the two independent approaches coded in yambo it will be useful to create two different folders for the input files.
Differently from other codes, the equations of motion of Yambo are in the length gauge and not in the velocity one. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of [https://arxiv.org/abs/1609.09639| https://arxiv.org/abs/1609.09639].
The Hamiltonian and the initial wave-functions are obtained from DFT. Then in order to obtain linear response we prove the system with a delta function field, that excites all the frequencies at the same footing, and Fourier transform the real-time polarization to get the response functions.


mkdir Inputs_rt
mkdir Inputs_nl


In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field.


=== Approach based on the density matrix ===


== Prerequisites ==
Use the command
The real-time response using the Time-Dependent Schroedinger Equation(TDSE) needs  <code>yambo_nl</code> and <code>ypp_nl</code> in double precision. In order to compile it, just add the flag <code>--enable-dp</code> in your <code>configure</code>. If you have problems in the compilation please have a look to [http://www.yambo-code.org/wiki/index.php?title=Installation compiling yambo].
  yambo_rt -n p -F Inputs_rt/01_td_ip.in


This tutorial on TDSE is divided into 8 steps:
to generate the input:


  negf                          # [R] Real-Time dynamics
  RT_Threads=0                  # [OPENMP/RT] Number of threads for real-time
  HXC_Potential= <span style="color:red">"IP"</span>          # [SC] SC HXC Potential
  % RTBands
    <span style="color:red">3</span> |  <span style="color:red">6</span> |                    # [RT] Bands
  %
  Integrator= "EULER RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
  PhLifeTime= 0.000000  fs      # [RT] Dephasing Time
  RTstep=10.000000      as      # [RT] Real Time step length
  NETime= 55.00000      fs      # [RT] Simulation Time
  % IOtime
  0.05    | 5.00    | 0.10    |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
  %
  % Field1_Freq
  0.00    | 0.00    | eV      # [RT Field1] Frequency
  %
  Field1_Int=<span style="color:red">1.E3  kWLm2</span>  # [RT Field1] Intensity
  Field1_Width= 0.000000 fs      # [RT Field1] Width
  Field1_kind= "<span style="color:red">DELTA</span>"          # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
  Field1_pol= "<span style="color:red">linear</span>"          # [RT Field1] Pol(linear|circular)
  % Field1_Dir
  0.000000 | <span style="color:red">1.000000</span> | 0.000000 |        # [RT Field1] Versor
  %
  % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
  %
  Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time


==DFT calculations==
Set the field direction along y, the field type to <code>DELTA</code>, the length of the simulation to 55 fs, number of bands from 3 to 6, dephasing to zero and the field intensity to 1.E3 [kW/cm2].
A small intensity is needed to ensure that we remain in the perturbative regime and that the response is dominated by linear term.
The <code>yambo_rt</code> is optimized for TD-SEX (or even more sophisticated calculations).


In this example, we will consider a single later of hexagonal boron nitride (hBN). The first input file is a self-consistent(SCF) calculation that is used to generate the density of the system. The second input file is a non-self consistent(NSCF) calculation to diagonalize the KS Hamiltonian, which depends on the density of the first run, on for a given number of bands and k-points. Notice that parameters in the NSCF calculation determine the number of k-points and the maximum number of bands that can be used in Lumen. Run this calculation with the command:
Now run the simulation:
  yambo_rt -F Inputs_rt/01_td_ip.in -J TD-IP_rt -C TD-IP_rt
The run produces, besides the standard report and (eventually) log files of yambo, 3 output files:
  TD-IP_rt/01_td_ip.in_TD-IP_rt
  TD-IP_rt/r-TD-IP_rt_negf
  TD-IP_rt/o-TD-IP_rt.polarization
  TD-IP_rt/o-TD-IP_rt.external_field
  TD-IP_rt/o-TD-IP_rt.current
Moreover it also makes a copy of the input file. If the run is taking to long you can open the copy of the input file <code>TD-IP_rt/01_td_ip.in_TD-IP_rt</code> and add there the string
STOP_NOW
It will finish the simulation in a proper way.


pw.x -inp hBN_2D_scf.in > output_scf
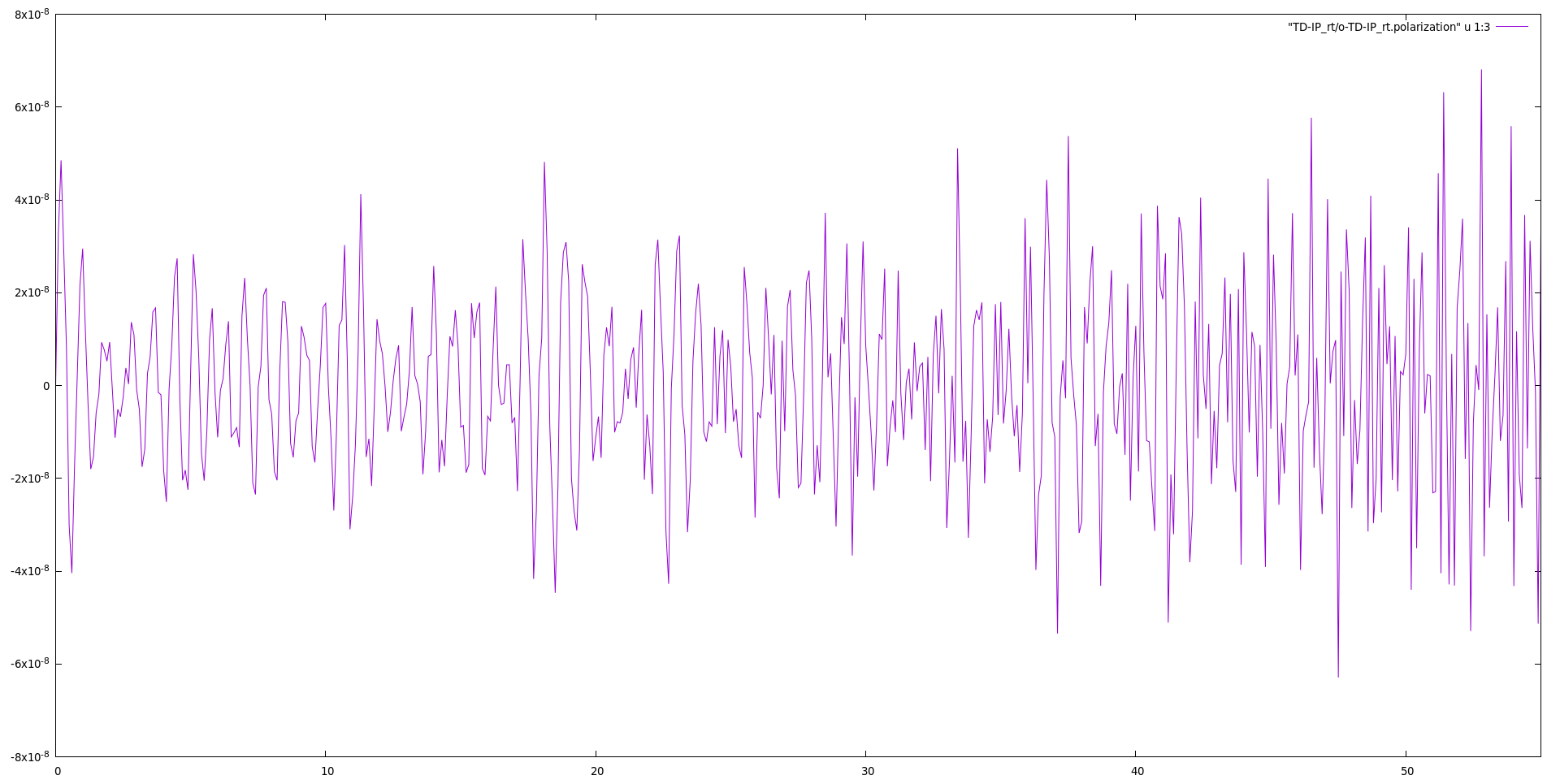
You can now plot the resulting time-dependent polarization and obtain something like this
  pw.x -inp hBN_2D_nscf.nscf.in > output_nscf
  gnuplot
  plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l


Notice that in the NSCF file of QuantumEspresso we use the flag <code>force_symmorphic=.true.</code> to exclude the non-symmorphic symmetries that are not supported by Yambo.
[[File:IP Polarization along y direction.png|thumb|center|900px|Time dependent polarization generated with a TD-IP run using yambo_rt]]


The polarization is oscillating very quickly and with the time step for the output file we have chosen (100 as) we can hardly resolve the oscillations. The slowest oscillation is expected at the first absorption peak, which is located slightly above 4 eV. This corresponds to a period of about 1 fs. Higher energy transitions are however also activated by the delta like pulse, which spans all frequencies (remember that the Fourier transform of a delta function is a constant).


==Import the wave-functions==
The I/O time, which is negligible in such calculations, is less optimized and becomes the most time demanding step here.
We can overcome this setting the IOtime for the polarization to 50 as (i.e. each 5 time steps). After the run you can have a look at the timing report and you will see that indeed most of the timing was spent in the I/O:
  RT databases IO :    6.8745 s CPU (    5501 calls,    0.0012 s avg)


If you used QuantumEspresso go in the folder <code>hBN_2D.save</code>. Then import the wave-function with the command
=== Approach based on the Berry Phase  ===


for QuantumEspresso:
Use the command
<code>
  yambo_nl -u n -F Inputs_nl/01_td_ip.in
p2y -F data-file.xml
</code>


to generate the input:


==Setup==
  nloptics                     # [R NL] Non-linear optics
 
Generate the setup input file with the command <code>yambo_nl -i -V RL -F setup.in</code>, then run yambo_nl -F setup.in. You can reduce the number of G-vectors in the setup in such a way to speed up calculations. I advise reducing G-vector to 1000 (about 50% of the initial ones).
 
 
==Reduce symmetries==
 
Since in real-time simulation we introduce a finite electric field in the Hamiltonian, the number of the symmetries of the original system is reduced due to the presence of this field. Using the tool <code>ypp -y</code> to generate the input file:
 
  fixsyms                      # [R] Reduce Symmetries
% Efield1
  0.00    | <span style="color:red">1.00</span>    | 0.00    |        # First external Electric Field
%
% Efield2
  0.00    | 0.00    | 0.00    |        # Additional external Electric Field
%
#RmAllSymm                  # Remove all symmetries
[[Variables#RmTimeRev|RmTimeRev]]                    # Remove Time Reversal
 
 
Set the external field in the y-direction and uncomment the Time Reversal flag, as shown in red above. Run <code>ypp</code> and it will create a new folder called <code>FixSymm</code> with the reduced symmetries wave-functions.
 
 
==Setup again==
 
Go in the <code>FixSymm</code> directory and run the setup again <code>yambo_nl -F ../setup.in</code>. Now everything is ready for the real-time simulations!
 
 
==Real-time dynamics==
 
In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field. Use the command <code>yambo_nl -u -F input_lr.in</code> to generate the input:
 
nlinear                     # [R NL] Non-linear optics
  NL_Threads= 1                # [OPENMP/NL] Number of threads for nl-optics
  NL_Threads= 1                # [OPENMP/NL] Number of threads for nl-optics
  % NLBands
  % NLBands
   <span style="color:red">3 |  6 </span>|                  # [NL] Bands
   <span style="color:red">3</span> |  <span style="color:red">6 </span>|                  # [NL] Bands
  %
  %
  NLstep=  0.0100      fs    # [NL] Real Time step length
  NLstep=  0.0100      fs    # [NL] Real Time step length
Line 94: Line 139:


          
          
The standard input of Lumen is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to <code>DELTA</code>, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red.
The standard input of <code>yambo_nl</code> is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to <code>DELTA</code>, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red.
We set the verbosity to "high" in such a way to print real-time output files.
We set the verbosity to "high" in such a way to print real-time output files.
We set the differential equation integrator to <code>INVINT</code> that is faster but less accurate than the default (see [https://arxiv.org/pdf/1310.7459.pdf PRB '''88''', 235113(R)]) . This integrator is ok in case of independent partcicles but I advise you to use <code>CRANKNIC</code> integrator when correlation effects are present. Now run yambo_nl -F input_lr.in
We set the differential equation integrator to <code>INVINT</code> that is faster but less accurate than the default (see Ref. <ref name="Attaccalite2013">C. Attaccalite and M. Gruning [https://arxiv.org/abs/1309.4012v2 Rev. B, '''88''', 235113 (2013)]</ref>) . This integrator is ok in case of independent particles but I advise you to use <code>CRANKNIC</code> integrator when correlation effects are present.
The code will produce different files: <code>o.polarization_F1</code> that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. If you plot the third column of <code>o.polarization_F1</code> versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:
Now run
  yambo_nl -F Inputs_nl/01_td_ip.in -J TD-IP_nl -C TD-IP_nl


The code will produce different files: <code>o.polarization_F1</code> that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation.
This time the simulation took much longer. This is the price to pay for computing the polarization with the Berry Phase technique. While there is no much gain in linear response, this will allow to compute also non linear coefficients which cannot be obtained with the density based approach. If we look at the time profile of the run we see:
  NL Berry Pol NEQ :  313.5414 s CPU (    5502 calls,    0.0570 s avg)
  SERIAL_inversion :  307.3369 s CPU ( 4402840 calls,    0.0001 s avg)
    NL Integrator :  87.6024 s CPU (    5501 calls,    0.0159 s avg)
SERIAL_lin_system :  85.9291 s CPU ( 1210220 calls,    0.0001 s avg)
Most of the time is spent computing the non-equilibrium Berry Polarization, which involves the inversion of small matrices via the Lapack inversion routine.
Some time is also required by the inversion solved which is coded via the solution of a linear system of equations as implemented in the Lapack library.
This integrator is more accurate than the Runge-Kutta 2nd order employed previously


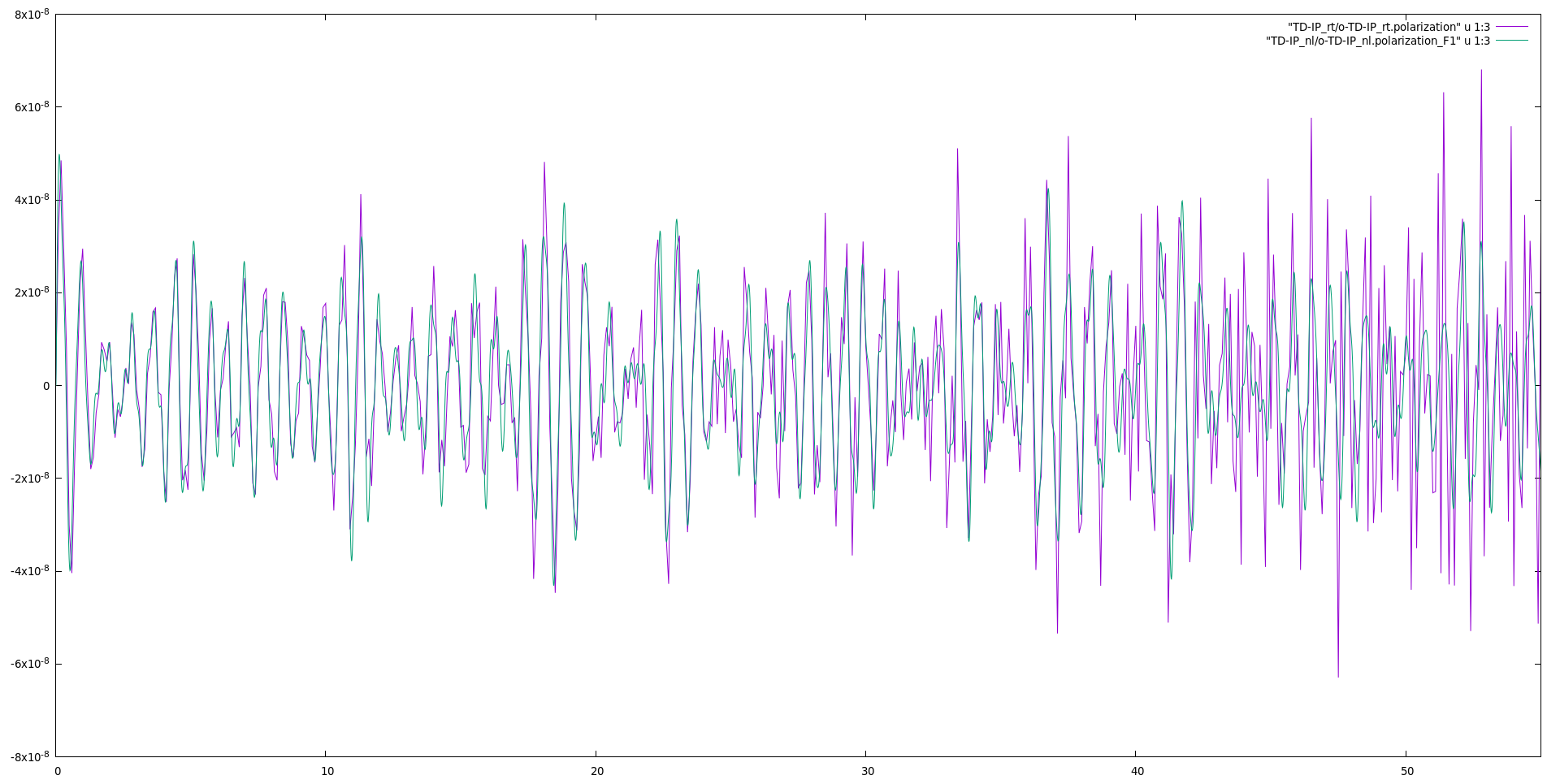
[[File:Bn polarization.png|center|600px|Real-time polarization in the y-direction]]
If you plot the third column of <code>o.polarization_F1</code> versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:


[[File:Bn polarization.png|thumb|center|900px|Real-time polarization in the y-direction]]


In the plot the polarization from the two different propagation schemes are compared.
There are few differences which could be due to the following reasons:
* Coupling with the external field: the <code>yambo_rt</code> evaluates the coupling with the external field through the dipoles (by default computing the commutator [x,Hnl]; the <code>yambo_nl</code> evaluates the coupling using an expression based on the Berry Phase. For the latter, a numerical differentiation in reciprocal space is performed. The 10x10 2D k-mesh may not be fine enough. For denser k-mesh, the Berry phase approach converges to the one based on the dipoles. To avoid this one can use <code>DipApproach="Covariant"</code> in the scheme used by yambo_rt.   
* Integrator: the integrator used for the <code>yambo_nl</code> is more accurate. The fact that the differences are more pronounced for long times may hint to inaccuracies in the integration of the equation of motions in <code>yambo_rt</code>. One can use a similar integrator with yambo_rt, by setting in input <code>Integrator= "INV RK2"</code>


==Results Analysis==
==Results Analysis==


Now we can use ypp_nl -u to analyze the results:
We can now proceed to the Fourier transform of the polarization to obtain the dielectric function
 
=== Approach based on the density matrix ===
 
Now we can use
  ypp_rt -n X -F Inputs_rt/ypp_abs.in
 
to generate the input file
  RealTime                      # [R] Real-Time Post-Processing
  RT_X                          # [R] Response functions Post-Processing
  Xorder=1                      # Max order of the response/exc functions
  % EnRngeRt
  0.00    | 10.00    | eV      # Energy range
  %
  ETStpsRt=1001                    # Total Energy steps
  % TimeRange
  0.00    | 0.00    | fs      # Time-window where processing is done
  %
DampMode= "<span style="color:red">LORENTZIAN</span>"            # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor=  <span style="color:red">0.10000</span>  eV    # Damping parameter
 
where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result.
Then we run
ypp_rt -F Inputs_rt/ypp_abs.in -J TD-IP_rt -C TD-IP_rt
and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization.
o-TD-IP_rt.YPP-eps_along_E
o-TD-IP_rt.YPP-eels_along_E
o-TD-IP_rt.YPP-polarization
o-TD-IP_rt.YPP-current
o-TD-IP_rt.YPP-E_frequency
inside the folder <code>TD-IP_rt</code>
 
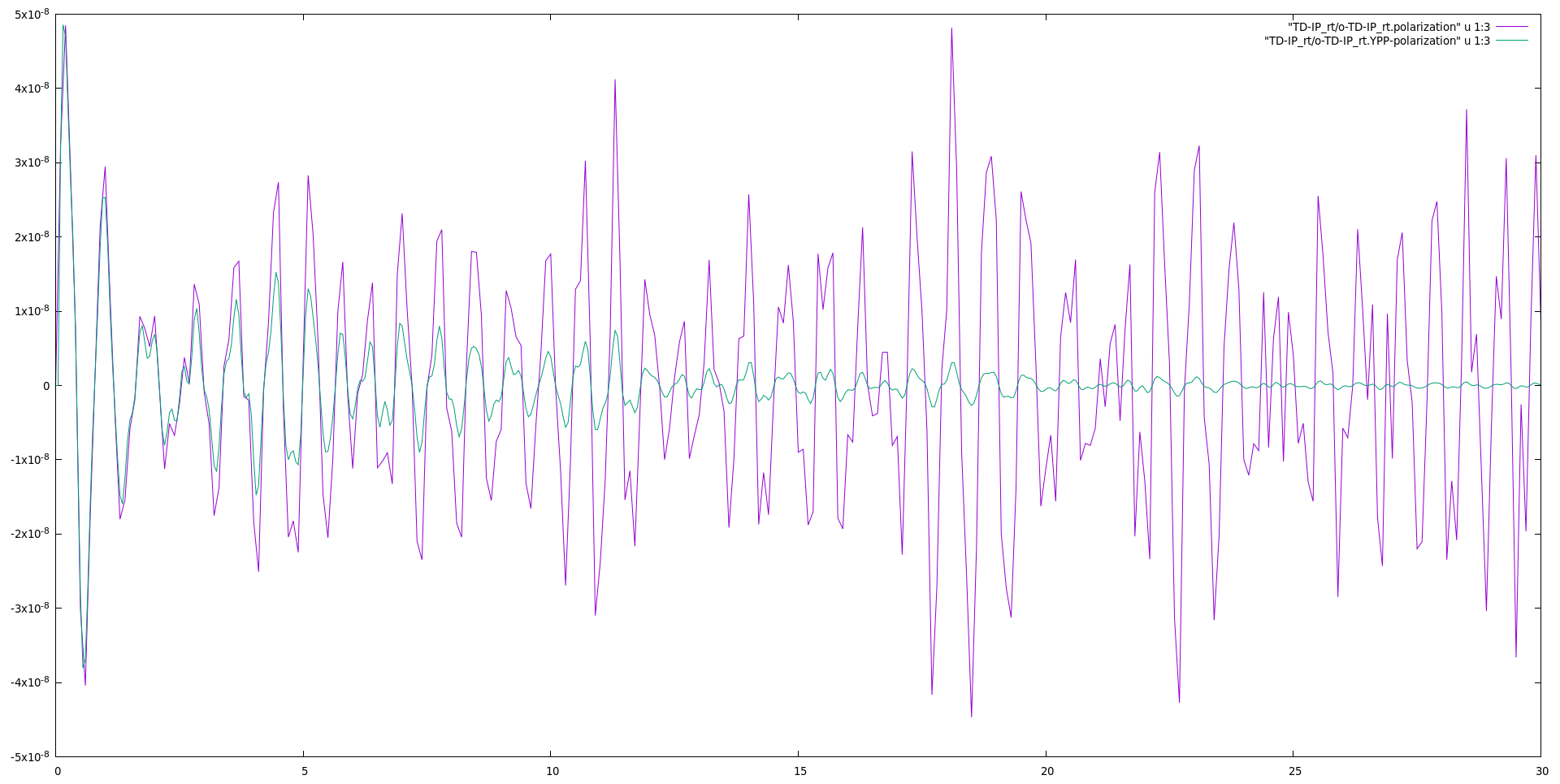
First let's have a look to the polarization.
gnuplot
plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l
replot "TD-IP_rt/o-TD-IP_rt.YPP-polarization" u 1:3 w l
We clearly see the effect of the Lorentzian damping added to the time dependent polarization
[[File:IP Polarization along y direction damped.png|thumb|center|900px|Time dependent polarization generated with the ypp_rt code. Comparing the damped polarization with the one produced by yambo_rt]]
 
Now we can plot the dielectric constant and compare it with the linear response:
 
 
=== Approach based on the Berry Phase  ===
 
 
Now we can use
  ypp_nl -u -F Inputs_nl/ypp_abs.in
 
to generate the input file:


  nonlinear                    # [R] NonLinear Optics Post-Processing
  nonlinear                    # [R] NonLinear Optics Post-Processing
Line 113: Line 221:
  -1.000000 |-1.000000 | fs    # Time-window where processing is done
  -1.000000 |-1.000000 | fs    # Time-window where processing is done
  %
  %
  ETStpsRt= 200               # Total Energy steps
  ETStpsRt= 1001               # Total Energy steps
  % EnRngeRt
  % EnRngeRt
   0.00000 | <span style="color:red">10.00000</span> | eV    # Energy range
   0.00000 | <span style="color:red">10.00000</span> | eV    # Energy range
Line 120: Line 228:
  DampFactor=  <span style="color:red">0.10000</span>  eV    # Damping parameter
  DampFactor=  <span style="color:red">0.10000</span>  eV    # Damping parameter


           
         
 
where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result.
where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result. Then we run <code>ypp_nl</code> and obtain the following files: the dielectric constant along with the field direction o.YPP-eps_along_E, the EELS along with the same direction o.YPP-eels_along_E, and the damped polarization o.YPP-damped_polarization.
Then we run
ypp_nl -F Inputs_nl/ypp_abs.in -J TD-IP_nl -C TD-IP_nl
and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization.
o-TD-IP_nl.YPP-eps_along_E
o-TD-IP_nl.YPP-eels_along_E
o-TD-IP_nl.YPP-damped_polarization
inside the folder <code>TD-IP_nl</code>
Now we can plot the dielectric constant and compare it with the linear response:
Now we can plot the dielectric constant and compare it with the linear response:
gnuplot
plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l
rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l
rep "TD-IP_nl/o-TD-IP_nl.YPP-eps_along_E" u 1:2 w l


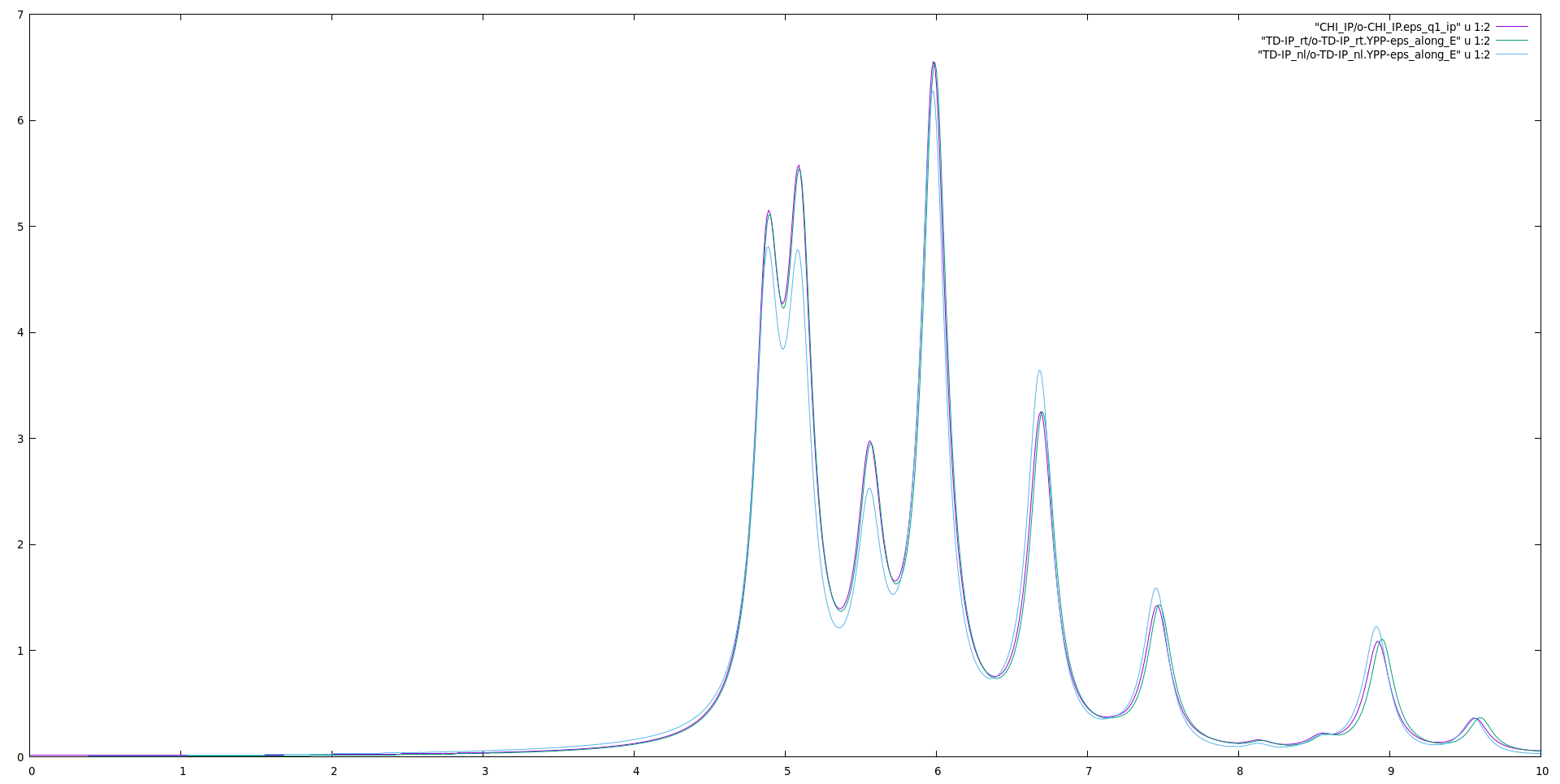
[[File:Bn optics.png|600px|center|Imaginary part of the dielectric constant]]
[[File:Bn optics.png|thumb|900px|center|Imaginary part of the dielectric constant]]


The input for the linear response can be downloaded [[http://www.attaccalite.com/lumen/tutorials/linear_optics_BNsheet.inorials/linear_optics_BNsheet.in|here]]. Notice that in a real-time simulation we obtain directly the
At low energy the post processing of <code>yambo_rt</code> are closer to the linear response approach, since they both share the same dipoles. At higher energies however the post processing of <code>yambo_nl</code> gives a better description of the energies, probably due to the better integrator. One can try to use the inversion integrator with <code>yambo_rt</code> or the covariant dipoles in linear response to better understand these differences.


<math> \chi(\omega) = \frac{P(\omega)}{E(\omega)} </math>
More info on this tutorial can be found in [http://www.attaccalite.com/lumen/linear_response.html here].


that is realted to the dielectric constant throught the relation <math>\epsilon(\omega) = 1 + 4 \pi \chi(\omega) </math>
<br>
{| style="width:100%" border="1"
|style="width:15%; text-align:left"|Prev: [[Prerequisites_for_Real_Time_propagation_with_Yambo|Prerequisites]]
|style="width:70%; text-align:center"|Now: [[Tutorials|Tutorials]] --> [[Linear response from real time simulations|Linear Response]] -->  [[Real time approach to linear response|Independent Particles ]]
|style="width:35%; text-align:right"|Next: [[Real time Bethe-Salpeter Equation (TDSE)]]
|-
|}

Latest revision as of 07:54, 21 October 2024

Introduction

In this example, we will consider a single layer of hexagonal boron nitride (hBN). If you didn't before you can download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz. and/or follow the instructions to generate the databases here: Prerequisites for Real Time propagation with Yambo

Before proceeding with the real-time simulations it is useful to compute the Independent Particles (IP) absorption spectrum of hBN along the y direction. If you didn't before create an Inputs folder and then the input file with the commands 

mkdir Inputs
yambo_nl -o c -F Inputs/01_ip.in

and set the proper input parameters 

 optics                         # [R OPT] Optics
 chi                            # [R CHI] Dyson equation for Chi.
 dipoles                        # [R   ] Compute the dipoles
 Chimod= "IP"                   # [X] IP/Hartree/ALDA/LRC/PF/BSfxc
 % QpntsRXd
    1 |  1 |                   # [Xd] Transferred momenta
 %
 % BndsRnXd
   3 | 6 |                     # [Xd] Polarization function bands
 %
 % EnRngeXd
   0.00000 | 20.00000 | eV      # [Xd] Energy range
 %
 % DmRngeXd
   0.10000 |  0.10000 | eV      # [Xd] Damping range
 %
 ETStpsXd= 2001                  # [Xd] Total Energy steps
 % LongDrXd
  0.000000 | 1.000000 | 0.000000 |        # [Xd] [cc] Electric Field
 %

and then run the code 

yambo_nl -F Inputs/01_ip.in -J CHI_IP -C CHI_IP

The resulting spectrum will give an idea of the energy involved in the real-time simulations 

gnuplot
gnuplot> plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l
Independent Particles absorptions for hBN comuting using 4 bands and with LDA eigenvalues

Real-time dynamics at the independent particles level

Since we work with the two independent approaches coded in yambo it will be useful to create two different folders for the input files. 

mkdir Inputs_rt
mkdir Inputs_nl

In order to calculate linear-response in real-time, we will perturb the system with a delta function in time external field.

Approach based on the density matrix

Use the command 

 yambo_rt -n p -F Inputs_rt/01_td_ip.in

to generate the input: 

 negf                           # [R] Real-Time dynamics
 RT_Threads=0                   # [OPENMP/RT] Number of threads for real-time
 HXC_Potential= "IP"           # [SC] SC HXC Potential
 % RTBands
   3 |  6 |                     # [RT] Bands
 %
 Integrator= "EULER RK2"              # [RT] Integrator. Use keywords space separated  ( "EULER/EXPn/INV" "SIMPLE/RK2/RK4/HEUN" "RWA")
 PhLifeTime= 0.000000   fs      # [RT] Dephasing Time
 RTstep=10.000000       as      # [RT] Real Time step length
 NETime= 55.00000       fs      # [RT] Simulation Time
 % IOtime
  0.05     | 5.00     | 0.10     |  fs    # [RT] Time between to consecutive I/O (OBSERVABLEs,CARRIERs - GF - OUTPUT)
 %
 % Field1_Freq
  0.00     | 0.00     | eV      # [RT Field1] Frequency
 %
 Field1_Int=1.E3   kWLm2   # [RT Field1] Intensity
 Field1_Width= 0.000000 fs      # [RT Field1] Width
 Field1_kind= "DELTA"           # [RT Field1] Kind(SIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
 Field1_pol= "linear"           # [RT Field1] Pol(linear|circular)
 % Field1_Dir
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor
 %
 % Field1_Dir_circ
  0.000000 | 1.000000 | 0.000000 |        # [RT Field1] Versor_circ
 %
 Field1_Tstart= 0.000000fs      # [RT Field1] Initial Time

Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6, dephasing to zero and the field intensity to 1.E3 [kW/cm2]. A small intensity is needed to ensure that we remain in the perturbative regime and that the response is dominated by linear term. The yambo_rt is optimized for TD-SEX (or even more sophisticated calculations).

Now run the simulation: 

 yambo_rt -F Inputs_rt/01_td_ip.in -J TD-IP_rt -C TD-IP_rt

The run produces, besides the standard report and (eventually) log files of yambo, 3 output files: 

 TD-IP_rt/01_td_ip.in_TD-IP_rt
 TD-IP_rt/r-TD-IP_rt_negf
 TD-IP_rt/o-TD-IP_rt.polarization
 TD-IP_rt/o-TD-IP_rt.external_field
 TD-IP_rt/o-TD-IP_rt.current

Moreover it also makes a copy of the input file. If the run is taking to long you can open the copy of the input file TD-IP_rt/01_td_ip.in_TD-IP_rt and add there the string 

STOP_NOW

It will finish the simulation in a proper way.

You can now plot the resulting time-dependent polarization and obtain something like this 

gnuplot
plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l
Time dependent polarization generated with a TD-IP run using yambo_rt

The polarization is oscillating very quickly and with the time step for the output file we have chosen (100 as) we can hardly resolve the oscillations. The slowest oscillation is expected at the first absorption peak, which is located slightly above 4 eV. This corresponds to a period of about 1 fs. Higher energy transitions are however also activated by the delta like pulse, which spans all frequencies (remember that the Fourier transform of a delta function is a constant).

The I/O time, which is negligible in such calculations, is less optimized and becomes the most time demanding step here. We can overcome this setting the IOtime for the polarization to 50 as (i.e. each 5 time steps). After the run you can have a look at the timing report and you will see that indeed most of the timing was spent in the I/O: 

 RT databases IO :    6.8745 s CPU (    5501 calls,    0.0012 s avg)

Approach based on the Berry Phase

Use the command 

 yambo_nl -u n -F Inputs_nl/01_td_ip.in

to generate the input: 

nloptics                      # [R NL] Non-linear optics
NL_Threads= 1                # [OPENMP/NL] Number of threads for nl-optics
% NLBands
  3 |  6 |                   # [NL] Bands
%
NLstep=   0.0100       fs    # [NL] Real Time step length
NLtime=55.000000      fs    # [NL] Simulation Time
NLverbosity= "high"           # [NL] Verbosity level (low | high)
NLintegrator= "INVINT"       # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC")
NLCorrelation= "IPA"         # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF")
NLLrcAlpha= 0.000000         # [NL] Long Range Correction
% NLEnRange
 0.200000 | 8.000000 | eV    # [NL] Energy range 
%
NLEnSteps= 1                 # [NL] Energy steps
NLDamping= 0.000000    eV    # [NL] Damping
% ExtF_Dir
 0.000000 | 1.000000  | 0.000000 |        # [NL ExtF] Versor
%
ExtF_kind=  "DELTA"          # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)


The standard input of yambo_nl is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red. We set the verbosity to "high" in such a way to print real-time output files. We set the differential equation integrator to INVINT that is faster but less accurate than the default (see Ref. [1]) . This integrator is ok in case of independent particles but I advise you to use CRANKNIC integrator when correlation effects are present. Now run 

 yambo_nl -F Inputs_nl/01_td_ip.in -J TD-IP_nl -C TD-IP_nl

The code will produce different files: o.polarization_F1 that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation. This time the simulation took much longer. This is the price to pay for computing the polarization with the Berry Phase technique. While there is no much gain in linear response, this will allow to compute also non linear coefficients which cannot be obtained with the density based approach. If we look at the time profile of the run we see: 

 NL Berry Pol NEQ :  313.5414 s CPU (    5502 calls,    0.0570 s avg)
 SERIAL_inversion :  307.3369 s CPU ( 4402840 calls,    0.0001 s avg)
    NL Integrator :   87.6024 s CPU (    5501 calls,    0.0159 s avg)
SERIAL_lin_system :   85.9291 s CPU ( 1210220 calls,    0.0001 s avg)

Most of the time is spent computing the non-equilibrium Berry Polarization, which involves the inversion of small matrices via the Lapack inversion routine. Some time is also required by the inversion solved which is coded via the solution of a linear system of equations as implemented in the Lapack library. This integrator is more accurate than the Runge-Kutta 2nd order employed previously

If you plot the third column of o.polarization_F1 versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:

Real-time polarization in the y-direction

In the plot the polarization from the two different propagation schemes are compared. There are few differences which could be due to the following reasons:

  • Coupling with the external field: the yambo_rt evaluates the coupling with the external field through the dipoles (by default computing the commutator [x,Hnl]; the yambo_nl evaluates the coupling using an expression based on the Berry Phase. For the latter, a numerical differentiation in reciprocal space is performed. The 10x10 2D k-mesh may not be fine enough. For denser k-mesh, the Berry phase approach converges to the one based on the dipoles. To avoid this one can use DipApproach="Covariant" in the scheme used by yambo_rt.
  • Integrator: the integrator used for the yambo_nl is more accurate. The fact that the differences are more pronounced for long times may hint to inaccuracies in the integration of the equation of motions in yambo_rt. One can use a similar integrator with yambo_rt, by setting in input Integrator= "INV RK2"

Results Analysis

We can now proceed to the Fourier transform of the polarization to obtain the dielectric function

Approach based on the density matrix

Now we can use 

 ypp_rt -n X -F Inputs_rt/ypp_abs.in

to generate the input file 

 RealTime                       # [R] Real-Time Post-Processing
 RT_X                           # [R] Response functions Post-Processing
 Xorder=1                       # Max order of the response/exc functions
 % EnRngeRt
  0.00     | 10.00     | eV      # Energy range
 %
 ETStpsRt=1001                     # Total Energy steps
 % TimeRange
  0.00     | 0.00     | fs      # Time-window where processing is done
 %
DampMode= "LORENTZIAN"             # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor=  0.10000   eV    # Damping parameter

where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result. Then we run 

ypp_rt -F Inputs_rt/ypp_abs.in -J TD-IP_rt -C TD-IP_rt

and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization. 

o-TD-IP_rt.YPP-eps_along_E
o-TD-IP_rt.YPP-eels_along_E
o-TD-IP_rt.YPP-polarization
o-TD-IP_rt.YPP-current
o-TD-IP_rt.YPP-E_frequency

inside the folder TD-IP_rt

First let's have a look to the polarization. 

gnuplot
plot "TD-IP_rt/o-TD-IP_rt.polarization" u 1:3 w l
replot "TD-IP_rt/o-TD-IP_rt.YPP-polarization" u 1:3 w l

We clearly see the effect of the Lorentzian damping added to the time dependent polarization

Time dependent polarization generated with the ypp_rt code. Comparing the damped polarization with the one produced by yambo_rt

Now we can plot the dielectric constant and compare it with the linear response:


Approach based on the Berry Phase

Now we can use 

 ypp_nl -u -F Inputs_nl/ypp_abs.in

to generate the input file: 

nonlinear                    # [R] NonLinear Optics Post-Processing
Xorder= 1                    # Max order of the response functions
% TimeRange
-1.000000 |-1.000000 | fs    # Time-window where processing is done
%
ETStpsRt= 1001                # Total Energy steps
% EnRngeRt
  0.00000 | 10.00000 | eV    # Energy range
%
DampMode= "LORENTZIAN"             # Damping type ( NONE | LORENTZIAN | GAUSSIAN )
DampFactor=  0.10000   eV    # Damping parameter


where we set a Lorentzian smearing corresponding to 0.1 eV. Notice that due to the finite time of our simulation smearing is always necessary to Fourier transform the result. Then we run 

ypp_nl -F Inputs_nl/ypp_abs.in -J TD-IP_nl -C TD-IP_nl

and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization. 

o-TD-IP_nl.YPP-eps_along_E
o-TD-IP_nl.YPP-eels_along_E
o-TD-IP_nl.YPP-damped_polarization

inside the folder TD-IP_nl Now we can plot the dielectric constant and compare it with the linear response: 

gnuplot
plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l
rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l
rep "TD-IP_nl/o-TD-IP_nl.YPP-eps_along_E" u 1:2 w l
Imaginary part of the dielectric constant

At low energy the post processing of yambo_rt are closer to the linear response approach, since they both share the same dipoles. At higher energies however the post processing of yambo_nl gives a better description of the energies, probably due to the better integrator. One can try to use the inversion integrator with yambo_rt or the covariant dipoles in linear response to better understand these differences.

More info on this tutorial can be found in here.


Prev: Prerequisites Now: Tutorials --> Linear Response --> Independent Particles Next: Real time Bethe-Salpeter Equation (TDSE)
  1. ↑ C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)
Retrieved from "https://wiki.yambo-code.eu/wiki/index.php?title=Real_time_approach_to_linear_response&oldid=8101"