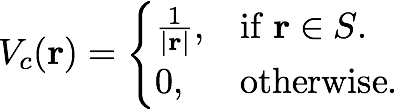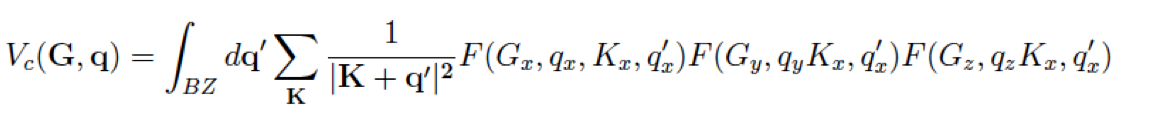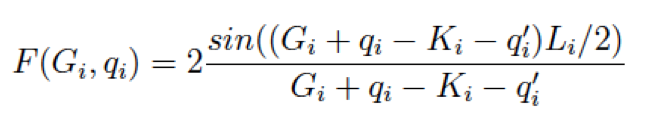How to treat low dimensional systems

In this tutorial you will learn how to:

• Avoid numerical divergences using the Random Integration Method (RIM)
• Generate a truncated coulomb potential with a box-like cutoff to eliminate the image-image interactions
• Use the truncated coulomb potential in the GW calculation
• Use the truncated coulomb potential in the BSE calculation
• Analyze the difference with corresponding calculations without the use of a truncated potetnial

Prerequisites

• SAVE folder for 2D hBN generated with a 6x6x1 k-grid
• yambo executable
• ypp executable
• gnuplot, for plotting spectra
• Complete the Generating the Yambo databases tutorial
• Run Initialization

Avoid numerical divergences using the Random Integration Method (RIM)

In DFT runs of low-dimensional materials low dimensional k-grids are generally used. (i.e. NxNx1 for a 2D sheet perpendicular to the z direction) This can create numerical problems in the convergence of the many-body results due to the divergence at small q of the coulomb potential (which appears in all the main equations, see i.e. the exchange self-energy equation).

To eliminate this problem YAMBO uses the so-called Random Integration Method which means to use a Monte Carlo Integration with Random Q-points whose number RandQpts is given in input.

Create the input to generate the ndb.RIM database

$ yambo -F yambo_RIM.in -r 

and change the following variable

 RandQpts= 1000000            # [RIM] Number of random q-points in the BZ
 RandGvec= 100            RL    # [RIM] Coulomb interaction RS components 

N.B RandGvec=100 means to use the RIM for the first 100 G-components of the coulomb potential (Suggestion : later you can check convergence of the HF gap changing these two values)

Close input and Run yambo

$ yambo -F yambo_RIM.in -J 2D

At the end in the 2D directory you find a new database A new report file r-2D_rim_cut is present. Open it and look inside

[04.02] RIM integrals

 =====================

 Gamma point sphere radius         [au]:  0.08028
 Points outside the sphere             :  800231
 [Int_sBZ(q=0) 1/q^2]*(Vol_sBZ)^(-1/3) = 7.667102
                                should be < 7.795600
 [WR./2D//ndb.RIM]-------------------------------------------
  Brillouin Zone Q/K grids (IBZ/BZ):   7   36    7   36
  Coulombian RL components        : 209
  Coulombian diagonal components  :yes
  RIM random points               : 1000000
  RIM  RL volume             [a.u.]: 0.390129
  Real RL volume             [a.u.]: 0.390112
  Eps^-1 reference component       :0
  Eps^-1 components                : 0.00      0.00      0.00
  RIM anysotropy factor            : 0.000000
 - S/N 005962 -------------------------- v.04.01.02 r.00120 -

 Summary of Coulomb integrals for non-metallic bands |Q|[au] RIM/Bare:

 Q [1]:0.1000E-40.9835 * Q [2]: 0.256404 1.093779
 Q [5]: 0.444104 1.031700 * Q [3]: 0.512807 1.023425
 Q [6]: 0.678380 1.013439 * Q [4]: 0.769211 1.010447
 Q [7]: 0.888208 1.007869

If you perform the HF calculation without generating and reading the ndb.RIM database you will have an HF gap of 12.91

Unfortunately the presence of the numerical instability is evident only using denser k-grids with respect to that one used in this Tutorial (6x6x1). To see it you should generate other SAVE directories with denser k-grids and check the HF gap.

To show the problem the HF gap calculated with different k-grids without (noRIM) and with Random Inetgration Method (RIM) are reported:

            noRIM   RIM
 6x6x1  
 12x12x1
 15x15x1
 45x45x1 

So home message : use always the RIM in MB simulations of low-dimensional materials.

Generate a truncated coulomb potential/ndb.cutoff database (yambo -r)

To simulate an isolated nano-material a convergence with cell vacuum size is in principle required, like in the DFT runs. The use of a truncated Coulomb potential allows to achieve faster convergence eliminating the interaction between the repeated images along the non-periodic direction (see i.e. D. Varsano et al Phys. Rev. B and .. ) In this tutorial we learn how to generate a box-like cutoff for a 2D system with the non-periodic direction along z.

In YAMBO you can use :

spherical   cutoff (for 0D systems)  
cylindrical cutoff (for 1D systems) 
box-like    cutoff (for 0D, 1D and 2D systems)

The Coulomb potential with a box-like cutoff is defined as

Then the FT component is

where

For a 2D-system with non period direction along z-axis we have

Important remarks:

• the Random Integration Method (RIM) is required to perform the Q-space integration
• for sufficiently large supercells a choose L_i slightly smaller than the cell size in the i-direction ensures to avoid interaction between replicas

Creation of the input file:

$ yambo -F yambo_cut2D.in  -r

Open the input file yambo_cut2D.in

Change the variables inside as:

RandQpts= 1000000          # [RIM] Number of random q-points in the BZ
RandGvec= 100        RL    # [RIM] Coulomb interaction RS components

CUTGeo= "box z"            # [CUT] Coulomb Cutoff geometry: box/cylinder/sphere X/Y/Z/XY..
% CUTBox
 0.00     | 0.00     | 32.0    |        # [CUT] [au] Box sides

Close the input file

Run yambo:

$ yambo -F  yambo_cut2D.in  -J 2D

in the directory 2D you will find the two new databases

ndb.RIM		ndb.cutoff