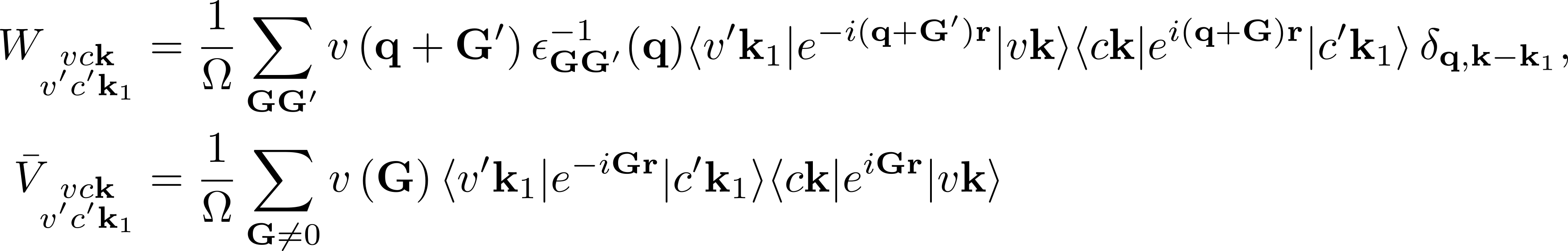Bethe-Salpeter kernel: Difference between revisions
No edit summary |
|||
| (39 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
''Prerequisites'' | In this module you will learn how to calculate the matrix elements of the Bethe-Salpeter kernels. This is a fundamental step in the calculation of optical spectra within the Bethe-Salpeter equation framework. | ||
==Background== | |||
To solve the Bethe-Salpeter equation, the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. | |||
For a non spin-polarized system and in the q=0 limit, the two-particle Hamiltonian matrix elements are given by | |||
[[File:BSE1-Eq1.png|none|x50px]] | |||
where ''vc'''''k''' indicates the pair of quasiparticle states ''v'''''k''' and ''c'''''k'''. | |||
The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part ''V'' (which stems from the Hartree potential) and the electron-hole attraction part ''W'' (which stems from the screened exchange potential). The kernel both shifts (diagonal contributions) and couples (off-diagonal contributions) the quasiparticle energy differences: | |||
[[File:BSE1_Eq3.png|none|x100px]] | |||
Here ε<sub>GG'</sub><sup>-1</sup> is the inverse of the dielectric screening matrix which was evaluated in the [[Static screening]] module. | |||
==Prerequisites== | |||
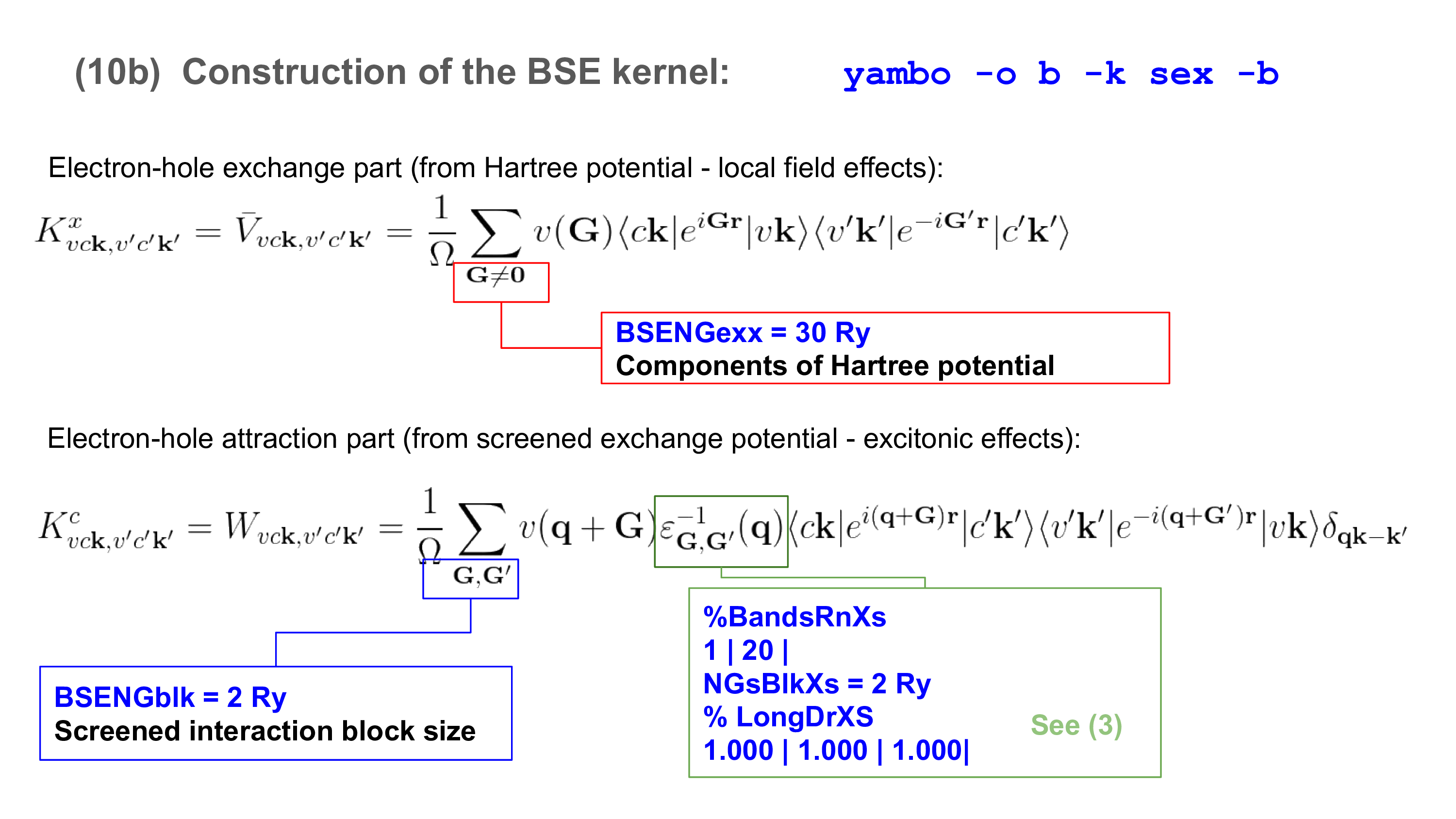
[[File:Yambo-handbook-v4.1.2-p-14.png|thumb|Cheatsheet on BSE Kernel|150px]] | |||
* You must first complete the [[Static screening|static screening]] module | |||
'''You will need''': | |||
* The <code>SAVE</code> databases for 3D hBN | |||
* The <code>3D_BSE</code> directory with the databases generated in the [[Static screening|static screening]] module | |||
* The <code>yambo</code> executable | |||
==Choosing input parameters== | |||
Generate the input file by invoking yambo with the option <code>-o b -k sex</code> from the command line: | |||
$ yambo -o b -k sex -F 02_3D_BSE_kernel.in -J 3D_BSE | |||
The input opens in the standard editor. The relevant input parameters to be changed are | |||
[[Variables#BSENGexx|BSENGexx]] = 30000 mRy | |||
[[Variables#BSENGBlk|BSENGBlk]] = 4000 mRy | |||
% [[Variables#BSEBands|BSEBands]] | |||
6 | 10 | | |||
% | |||
The first two are the cutoff for the summations on the reciprocal lattice vectors which appear in the expressions for ''V'' (BSENGexx) and ''W'' (BSENGBlk) here above. | |||
The third parameter gives the range of quasiparticle states (their band index) that define the basis of quasiparticle pairs that we need to describe the excitons (in the energy range of interest). | |||
For example since we have 8 occupied bands, here we consider the pairs of bands: ''6-9'', ''6-10'', ''7-9'', ''7-10'', ''8-9'', ''8-10'' (those are 6 pairs of bands = 3 valence times 2 conduction bands). | |||
For each of those pairs we then consider all '''k''' points in the Brillouin zone available from the DFT calculations. Since we have a ''6 x 6 x 2'' grid, this amounts to 72 '''k''' points in the Brillouin zone. | |||
Then finally we are using a basis of ''6 x 72 = 432'' ''vc'''''k''' pairs to represent the excitons of the system. | |||
The values for these 3 parameters are chosen from convergence studies, as discussed in the [[How to choose the input parameters|next tutorial]]. | |||
==Bethe-Salpeter kernel runlevel== | |||
Run the calculation by invoking yambo in the command line: | |||
$ yambo -F 02_3D_BSE_kernel.in -J 3D_BSE | |||
In the log (either in standard output or in <code>l-3D_BSE_optics_dipoles_bse</code>), after various setup/loading, the kernel is calculated: | |||
<01s> [05.03.03] Main kernel loop | |||
<02s> Kernel |########################################| [100%] --(E) --(X) | |||
In the report <code>r-3D_BSE_optics_dipoles_bse</code> the information relative to this runlevel are reported under the section: | |||
[05] Bethe Salpeter Equation @q1 | |||
================================ | |||
<!-- | |||
[05] Response Functions in Transition space | |||
=========================================== | |||
(yambo 4.3) | |||
[05] BSE solver(s) @q1 | |||
========================= | |||
(yambo 4.5) | |||
--> | |||
Take some time to inspect the log and the report. For example try to find where the input parameters are reported, the dimension of the 2-particle Hamiltonian and if these match your expectations. | |||
This run does not produce any human readable output. The kernel is stored in a database in the 3D_BSE directory | |||
3D_BSE/ndb.BS_Q1 | |||
==Summary== | |||
From this tutorial you've learned: | |||
* How to compute the Bethe-Salpeter kernel | |||
==Navigate== | |||
* Previous module: [[Static screening]] | |||
* Next module: [[Bethe-Salpeter solver: diagonalization | Bethe-Salpeter solver: diagonalization]] | |||
* Back to [[Calculating optical spectra including excitonic effects: a step-by-step guide]] tutorial | |||
* [[Tutorials|Back to tutorials menu]] | |||
* [[Modules|Back to technical modules menu]] | |||
<!--''Prerequisites'' | |||
Run [[Initialization]] | Run [[Initialization]] | ||
| Line 11: | Line 100: | ||
''Create the input'' | ''Create the input'' | ||
$ yambo -F 03_bse_Ws.in -b -o b -k sex -V qp (for a 3D) | $ yambo -F 03_bse_Ws.in -b -o b -k sex -V qp -J 3D (for a 3D) | ||
or | or | ||
$ yambo -F 03_bse_Ws_2D.in -b -o b -k sex -V qp -r (for a 2D) | $ yambo -F 03_bse_Ws_2D.in -b -o b -k sex -V qp -r -J 2D (for a 2D) | ||
Open it and change some of the input variables | Open it and change some of the input variables | ||
First change BSEBands which specify the range of bands to be used in the construction of the BS kernel | |||
Remember that the BS kernel is written in Bloch space and its size is given by | |||
BS kernel size = Valence Bands × Conduction Bands × K-points in the whole BZ | |||
For h-BN put: | |||
% BSEBands | |||
4 | 12 | # [BSK] Bands range | |||
For h-BN 2D put: | |||
% BSEBands | |||
2 | 6 | # [BSK] Bands range | |||
Then change the number of G-components (in number of RL or in energy cutoff) for the exchange(BSENGexx) and correlation (BSENGBlk) part of the BS kernel | |||
Both for h-BN or h-BN 2D put | |||
BSENGexx= 30 Ry # [BSK] Exchange components | BSENGexx= 30 Ry # [BSK] Exchange components | ||
BSENGBlk= 2 Ry # [BSK] Screened interaction block size | BSENGBlk= 2 Ry # [BSK] Screened interaction block size | ||
The GW energies are required in the excitonic hamiltonian. | |||
If the rigid scissor assumption is a good approximation for the material of interest | |||
the simplest way is to give the value of the minimum GW correction precalculated by you or found in the literature. | |||
For hBN bulk: | |||
% KfnQP_E | |||
value0000 | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim | |||
For hBN | For hBN-2D: | ||
% KfnQP_E | % KfnQP_E | ||
value | 1.000000 | 1.000000 | # [EXTQP BSK BSS] E parameters (c/v) eV|adim|adim | |||
Note that if you know also the values of the conduction and valence stretching you can insert them instead of using the default values of 1. | |||
Instead, if you have already generated a ndb.QP database for the full set of k-points and energies of the excitonic Hamiltonian, | |||
you can read it in this way | |||
for hBN bulk: | |||
KfnQPdb= " E < ./3D/ndb.QP " # [EXTQP BSK BSS] Database | |||
for hBN-2D: | |||
KfnQPdb= " E < ./2D/ndb.QP " # [EXTQP BSK BSS] Database | |||
Close | Close the input and run the code | ||
$ yambo -F 03_bse_Ws.in | $ yambo -F 03_bse_Ws.in -J 3D ( for 3D) | ||
or | or | ||
$ yambo -F 03_bse_Ws_2D.in (for 2D) | $ yambo -F 03_bse_Ws_2D.in -J 2D (for 2D) | ||
--> | |||
Latest revision as of 12:56, 24 May 2023
In this module you will learn how to calculate the matrix elements of the Bethe-Salpeter kernels. This is a fundamental step in the calculation of optical spectra within the Bethe-Salpeter equation framework.
Background
To solve the Bethe-Salpeter equation, the latter is usually rewritten in the space of transitions between valence and conduction states as the (pseudo)eigenvalue problem for a two-particle Hamiltonian. For a non spin-polarized system and in the q=0 limit, the two-particle Hamiltonian matrix elements are given by
where vck indicates the pair of quasiparticle states vk and ck. The first term on the RHS is the quasiparticle energy differences (diagonal only). The second term is the kernel which is the sum of the electron-hole exchange part V (which stems from the Hartree potential) and the electron-hole attraction part W (which stems from the screened exchange potential). The kernel both shifts (diagonal contributions) and couples (off-diagonal contributions) the quasiparticle energy differences:
Here εGG'-1 is the inverse of the dielectric screening matrix which was evaluated in the Static screening module.
Prerequisites
- You must first complete the static screening module
You will need:
- The
SAVEdatabases for 3D hBN - The
3D_BSEdirectory with the databases generated in the static screening module - The
yamboexecutable
Choosing input parameters
Generate the input file by invoking yambo with the option -o b -k sex from the command line:
$ yambo -o b -k sex -F 02_3D_BSE_kernel.in -J 3D_BSE
The input opens in the standard editor. The relevant input parameters to be changed are
BSENGexx = 30000 mRy BSENGBlk = 4000 mRy % BSEBands 6 | 10 | %
The first two are the cutoff for the summations on the reciprocal lattice vectors which appear in the expressions for V (BSENGexx) and W (BSENGBlk) here above.
The third parameter gives the range of quasiparticle states (their band index) that define the basis of quasiparticle pairs that we need to describe the excitons (in the energy range of interest). For example since we have 8 occupied bands, here we consider the pairs of bands: 6-9, 6-10, 7-9, 7-10, 8-9, 8-10 (those are 6 pairs of bands = 3 valence times 2 conduction bands).
For each of those pairs we then consider all k points in the Brillouin zone available from the DFT calculations. Since we have a 6 x 6 x 2 grid, this amounts to 72 k points in the Brillouin zone.
Then finally we are using a basis of 6 x 72 = 432 vck pairs to represent the excitons of the system.
The values for these 3 parameters are chosen from convergence studies, as discussed in the next tutorial.
Bethe-Salpeter kernel runlevel
Run the calculation by invoking yambo in the command line:
$ yambo -F 02_3D_BSE_kernel.in -J 3D_BSE
In the log (either in standard output or in l-3D_BSE_optics_dipoles_bse), after various setup/loading, the kernel is calculated:
<01s> [05.03.03] Main kernel loop <02s> Kernel |########################################| [100%] --(E) --(X)
In the report r-3D_BSE_optics_dipoles_bse the information relative to this runlevel are reported under the section:
[05] Bethe Salpeter Equation @q1 ================================
Take some time to inspect the log and the report. For example try to find where the input parameters are reported, the dimension of the 2-particle Hamiltonian and if these match your expectations.
This run does not produce any human readable output. The kernel is stored in a database in the 3D_BSE directory
3D_BSE/ndb.BS_Q1
Summary
From this tutorial you've learned:
- How to compute the Bethe-Salpeter kernel
- Previous module: Static screening
- Next module: Bethe-Salpeter solver: diagonalization
- Back to Calculating optical spectra including excitonic effects: a step-by-step guide tutorial
- Back to tutorials menu
- Back to technical modules menu