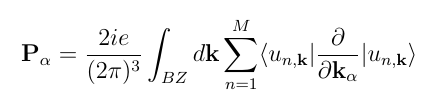Dielectric function from Bloch-states dynamics: Difference between revisions
No edit summary |
|||
| Line 27: | Line 27: | ||
* by including all terms, one selects the ''time-dependent Screened-exchange or Bethe-Salpeter equation'' level of theory. | * by including all terms, one selects the ''time-dependent Screened-exchange or Bethe-Salpeter equation'' level of theory. | ||
The type of "experiment" to perform, or of the response one would like to extract, depend on the time-dependent field in input and the post-processing of the Berry's phase polarization. | The type of "experiment" to perform, or of the response one would like to extract, depend on the time-dependent field in input and the post-processing of the Berry's phase polarization. The induced polarization is the sum of the responses of the system to all orders in the external field: | ||
<math>\bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{P}_n (t) </math> | |||
In the case we are interested in linear response only, we use a delta-like electric field that excites all frequencies of the system. We choose the intensity of the field <math>E</math> to be weak enough so that the response is dominated by the first order term. The response at all frequencies is obtained by taking the Fourier-transform of the polarization as | |||
<math> \chi(\omega) = \frac{P(\omega)}{E} </math>. | |||
The response <math> \chi</math> is related to the dielectric function through the relation <math>\epsilon(\omega) = 1 + 4 \pi \chi(\omega) </math>. | |||
See also Ref. <ref name="Attaccalite2013"></ref>. | |||
== Notes: == | == Notes: == | ||
| Line 43: | Line 52: | ||
Similar to what you have seen in the tutorial for the density matrix formalism ([[Real time approach to linear response]]) we start from the lowest level of theory. Here it is assumed you ran the tutorial on the density-matrix formalism and so you are familiar with the optical spectrum of 2D h-BN at this level of theory. You will recognise that the input and output for the Bloch-state formalism are very similar to those for the density-matrix formalism. | Similar to what you have seen in the tutorial for the density matrix formalism ([[Real time approach to linear response]]) we start from the lowest level of theory. Here it is assumed you ran the tutorial on the density-matrix formalism and so you are familiar with the optical spectrum of 2D h-BN at this level of theory. You will recognise that the input and output for the Bloch-state formalism are very similar to those for the density-matrix formalism. | ||
Use the command | == Run the simulations == | ||
Use the command: | |||
yambo_nl -u -F Inputs_nl/01_td_ip.in | yambo_nl -u -F Inputs_nl/01_td_ip.in | ||
| Line 94: | Line 105: | ||
* Dipoles: the <code>yambo_rt</code> evaluates the dipoles via [x,Hnl], the <code>yambo_nl</code> computes the dipoles via the Covariant approach. For the latter, a numerical differentiation in reciprocal space is performed. The 10x10 2D k-mesh may not be fine enough. For denser k-mesh, the dipoles obtained with the Covariant approach converge to those evaluated via [x,Hnl]. | * Dipoles: the <code>yambo_rt</code> evaluates the dipoles via [x,Hnl], the <code>yambo_nl</code> computes the dipoles via the Covariant approach. For the latter, a numerical differentiation in reciprocal space is performed. The 10x10 2D k-mesh may not be fine enough. For denser k-mesh, the dipoles obtained with the Covariant approach converge to those evaluated via [x,Hnl]. | ||
* Integrator: the integrator used for the <code>yambo_nl</code> is more accurate. The fact that the differences are more pronounced for long times may hint to inaccuracies in the integration of the equation of motions in <code>yambo_rt</code>. | * Integrator: the integrator used for the <code>yambo_nl</code> is more accurate. The fact that the differences are more pronounced for long times may hint to inaccuracies in the integration of the equation of motions in <code>yambo_rt</code>. | ||
== Output postprocessing: the dielectric function == | |||
Once we obtained the polarization, we Fourier transform the polarization to obtain the dielectric function. | |||
Use the command: | |||
ypp_nl -u -F Inputs_nl/ypp_abs.in | |||
to generate the input file: | |||
nonlinear # [R] NonLinear Optics Post-Processing | |||
Xorder= 1 # Max order of the response functions | |||
% TimeRange | |||
-1.000000 |-1.000000 | fs # Time-window where processing is done | |||
% | |||
ETStpsRt= 1001 # Total Energy steps | |||
% EnRngeRt | |||
0.00000 | <span style="color:red">10.00000</span> | eV # Energy range | |||
% | |||
DampMode= "<span style="color:red">LORENTZIAN</span>" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) | |||
DampFactor= <span style="color:red">0.10000</span> eV # Damping parameter | |||
where we set a Lorentzian smearing corresponding to 0.1 eV. Note that due to the finite time of our simulation, we need to introduce a finite smearing to Fourier transform the result. | |||
To run the post-processing, use the command: | |||
ypp_nl -F Inputs_nl/ypp_abs.in -J TD-IP_nl -C TD-IP_nl | |||
and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization. | |||
o-TD-IP_nl.YPP-eps_along_E | |||
o-TD-IP_nl.YPP-eels_along_E | |||
o-TD-IP_nl.YPP-damped_polarization | |||
inside the folder <code>TD-IP_nl</code> | |||
Now we can plot the dielectric constant and compare it with the linear response: | |||
gnuplot | |||
plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l | |||
rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l | |||
rep "TD-IP_nl/o-TD-IP_nl.YPP-eps_along_E" u 1:2 w l | |||
[[File:Bn optics.png|thumb|900px|center|Imaginary part of the dielectric constant]] | |||
In the low energy part of the spectrum, the dielectric function obtained from the <code>yambo_rt</code> is closer to that obtained from the linear response approach. This may due to the fact that they share the same dipoles while in <code>yambo_nl</code> those are obtained numerically. Instead, in the high energy part of the spectrum, the dielectric function obtained from the <code>yambo_nl</code> is closer to that obtained from the linear response approach. Likely, this is due to the better integrator used. | |||
To better understand these differences, one can use the inversion integrator with <code>yambo_rt</code>, the covariant dipoles in linear response. | |||
= References = | = References = | ||
<references/> | <references/> | ||
Revision as of 12:18, 19 May 2023
Step 0: Theoretical background
The dynamics of Bloch-states is found by integrating a set of Time Dependent Effective Schrödinger Equations (TD-ESEs). Effective means that an effective Hamiltonian is considered. We consider the many-body effective Hamiltonians seen in the Linear response from real time simulations. In addition, one can also consider effective Hamiltonians based on density-functional theory. The latter choice gives time-dependent density-functional theory.
At difference with what seen in Linear response from real time simulations, the coupling between electrons and the external field is described by means of the Modern Theory of Polarization:
Where [math]\displaystyle{ | v_{i \mathbf{k}} \rangle }[/math] are the time-dependent Bloch states (corresponding to the filled Bloch-states at zero-field), [math]\displaystyle{ \mathcal E(t) }[/math] is the external field and the term [math]\displaystyle{ i e \partial k }[/math] is the dipole operator consistent with periodic boundary condition. For more details on this last term, see Ref. [1] and [2].
[math]\displaystyle{ h_{rt} }[/math] is the Hamiltonian,
.
This contains the equilibrium Hamiltonian, that is the zero-field eigenvalues evaluated through DFT; the quasiparticle corrections, evaluated from GW or estimated from experiment, and the variation of the self-energy. The latter is a functional of the density matrix [math]\displaystyle{ \rho }[/math], which is obtained from the Bloch states.
From the solution of the equation of motion for the Bloch states, the polarization is calculated by means of Berry's phase
.
One can decide the level of theory by selecting the terms to include in the Hamiltonian:
- by including only the first term, one selects the independent-particle approximation
- by including the first and second terms, one selects the independent-quasiparticle approximation
- by including the first, second terms and the Hartree part of the self-energy, one selects the time-dependent Hartree or random-phase approximation
- by including all terms, one selects the time-dependent Screened-exchange or Bethe-Salpeter equation level of theory.
The type of "experiment" to perform, or of the response one would like to extract, depend on the time-dependent field in input and the post-processing of the Berry's phase polarization. The induced polarization is the sum of the responses of the system to all orders in the external field: [math]\displaystyle{ \bf{P}(t) = \sum_{n=-\infty}^{+\infty} \bf{P}_n (t) }[/math]
In the case we are interested in linear response only, we use a delta-like electric field that excites all frequencies of the system. We choose the intensity of the field [math]\displaystyle{ E }[/math] to be weak enough so that the response is dominated by the first order term. The response at all frequencies is obtained by taking the Fourier-transform of the polarization as
[math]\displaystyle{ \chi(\omega) = \frac{P(\omega)}{E} }[/math].
The response [math]\displaystyle{ \chi }[/math] is related to the dielectric function through the relation [math]\displaystyle{ \epsilon(\omega) = 1 + 4 \pi \chi(\omega) }[/math]. See also Ref. [2].
Notes:
- Length vs Velocity gauge: the equations of motion of Yambo are in the length gauge. Other codes choose instead to work in the velocity gauge. If you want to know more about the advantages and disadvantages of the two gauges read section 2.7 of Ref. [3].
- Advantages and disadvantages with respect to the density-matrix based formalism: Yambo implements two distinct formalisms for studying the real-time response, the one based on density-matrix and the one based on Boch states. Which formalism is best to use depends on what one wants to simulate. The dynamics formulation in terms of density matrix or non-equilibrium Green's functions allows a systematic treatment of correlation effects and electron-phonon coupling[4], but the price to pay is that the coupling with the external field is correct only to the linear order. This formalism is important in all those phenomena where electronic relaxation plays a major role. On the other hand, the formulation in terms of the Bloch states treats coupling with the external field in an exact way even beyond the linear regime, and for this reason, it allows the description of phenomena coherent with the external fields and to access, for example, non-linear responses.
Step 1: Prerequisites
In this example, we will consider a single layer of hexagonal boron nitride (hBN). Before running real time simulations in yambo you need to:
- download input files and Yambo databases for this tutorial here: hBN-2D-RT.tar.gz.
- perform the steps described in Prerequisites for Real Time propagation with Yambo.
Step 2: Independent-particle approximation
Similar to what you have seen in the tutorial for the density matrix formalism (Real time approach to linear response) we start from the lowest level of theory. Here it is assumed you ran the tutorial on the density-matrix formalism and so you are familiar with the optical spectrum of 2D h-BN at this level of theory. You will recognise that the input and output for the Bloch-state formalism are very similar to those for the density-matrix formalism.
Run the simulations
Use the command:
yambo_nl -u -F Inputs_nl/01_td_ip.in
to generate the input:
nloptics # [R NL] Non-linear optics NL_Threads= 1 # [OPENMP/NL] Number of threads for nl-optics % NLBands 3 | 6 | # [NL] Bands % NLstep= 0.0100 fs # [NL] Real Time step length NLtime=55.000000 fs # [NL] Simulation Time NLverbosity= "high" # [NL] Verbosity level (low | high) NLintegrator= "INVINT" # [NL] Integrator ("EULEREXP/RK4/RK2EXP/HEUN/INVINT/CRANKNIC") NLCorrelation= "IPA" # [NL] Correlation ("IPA/HARTREE/TDDFT/LRC/JGM/SEX/HF") NLLrcAlpha= 0.000000 # [NL] Long Range Correction % NLEnRange 0.200000 | 8.000000 | eV # [NL] Energy range % NLEnSteps= 1 # [NL] Energy steps NLDamping= 0.000000 eV # [NL] Damping % ExtF_Dir 0.000000 | 1.000000 | 0.000000 | # [NL ExtF] Versor % ExtF_kind= "DELTA" # [NL ExtF] Kind(SIN|SOFTSIN|RES|ANTIRES|GAUSS|DELTA|QSSIN)
The standard input of yambo_nl is thought for the non-linear response so we have to change some parameters in order to calculate the linear response. Set the field direction along y, the field type to DELTA, the length of the simulation to 55 fs, number of bands from 3 to 6 dephasing to zero and the number of energy steps to one, as shown above in red.
We set the verbosity to "high" in such a way to print real-time output files.
We set the differential equation integrator to INVINT that is faster but less accurate than the default (see Ref. [2]) . This integrator is ok in case of independent particles but I advise you to use CRANKNIC integrator when correlation effects are present.
Now run
yambo_nl -F Inputs_nl/01_td_ip.in -J TD-IP_nl -C TD-IP_nl
The code will produce different files: o.polarization_F1 that contains the polarization, o.external_potential_F1 the external field we used, and finally r_optics_nloptics a report with all information about the simulation.
This time the simulation took much longer. This is the price to pay for computing the polarization with the Berry Phase technique. While there is no much gain in linear response, this will allow computing also nonlinear coefficients, which cannot be obtained with the density based approach. If we look at the time profile of the run we see:
NL Berry Pol NEQ : 313.5414 s CPU ( 5502 calls, 0.0570 s avg)
SERIAL_inversion : 307.3369 s CPU ( 4402840 calls, 0.0001 s avg)
NL Integrator : 87.6024 s CPU ( 5501 calls, 0.0159 s avg)
SERIAL_lin_system : 85.9291 s CPU ( 1210220 calls, 0.0001 s avg)
Most of the time is spent computing the non-equilibrium Berry Polarization, which involves the inversion of small matrices via the Lapack inversion routine. Some time is also required by the inversion solved, which is coded via the solution of a linear system of equations as implemented in the Lapack library. This integrator is more accurate than the Runge-Kutta 2nd order employed previously
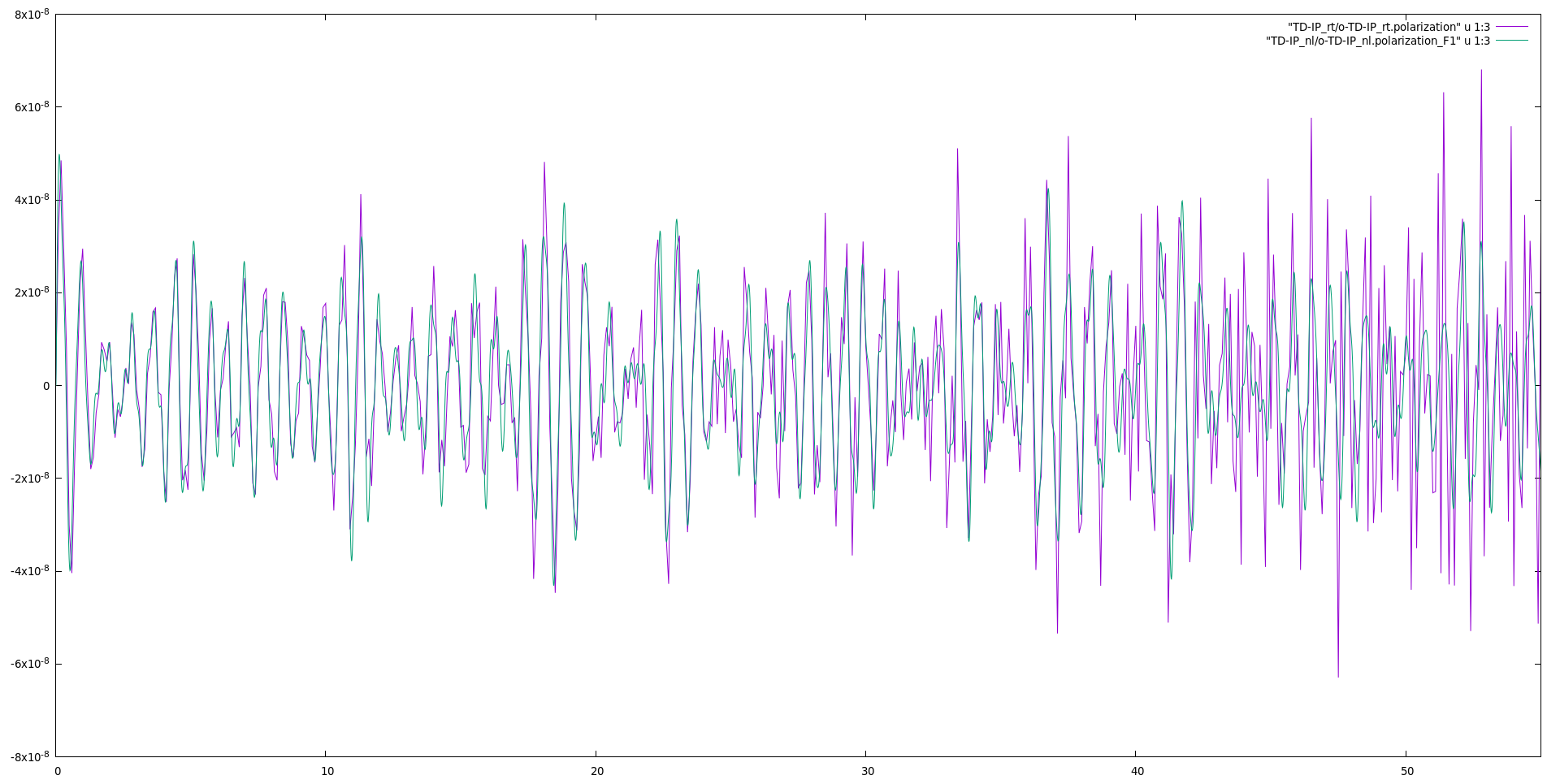
If you plot the third column of o.polarization_F1 versus the first one (time-variable) you will get the time-dependent polarization along the y-direction:
For comparison, in the figure above, the polarization is obtained either through the Bloch-states or the density-matrix. There are few differences which could be due to the following reasons:
- Dipoles: the
yambo_rtevaluates the dipoles via [x,Hnl], theyambo_nlcomputes the dipoles via the Covariant approach. For the latter, a numerical differentiation in reciprocal space is performed. The 10x10 2D k-mesh may not be fine enough. For denser k-mesh, the dipoles obtained with the Covariant approach converge to those evaluated via [x,Hnl]. - Integrator: the integrator used for the
yambo_nlis more accurate. The fact that the differences are more pronounced for long times may hint to inaccuracies in the integration of the equation of motions inyambo_rt.
Output postprocessing: the dielectric function
Once we obtained the polarization, we Fourier transform the polarization to obtain the dielectric function.
Use the command:
ypp_nl -u -F Inputs_nl/ypp_abs.in
to generate the input file:
nonlinear # [R] NonLinear Optics Post-Processing Xorder= 1 # Max order of the response functions % TimeRange -1.000000 |-1.000000 | fs # Time-window where processing is done % ETStpsRt= 1001 # Total Energy steps % EnRngeRt 0.00000 | 10.00000 | eV # Energy range % DampMode= "LORENTZIAN" # Damping type ( NONE | LORENTZIAN | GAUSSIAN ) DampFactor= 0.10000 eV # Damping parameter
where we set a Lorentzian smearing corresponding to 0.1 eV. Note that due to the finite time of our simulation, we need to introduce a finite smearing to Fourier transform the result.
To run the post-processing, use the command:
ypp_nl -F Inputs_nl/ypp_abs.in -J TD-IP_nl -C TD-IP_nl
and obtain the files for the dielectric constant along with the field direction, the EELS along with the same direction, and the damped polarization.
o-TD-IP_nl.YPP-eps_along_E o-TD-IP_nl.YPP-eels_along_E o-TD-IP_nl.YPP-damped_polarization
inside the folder TD-IP_nl
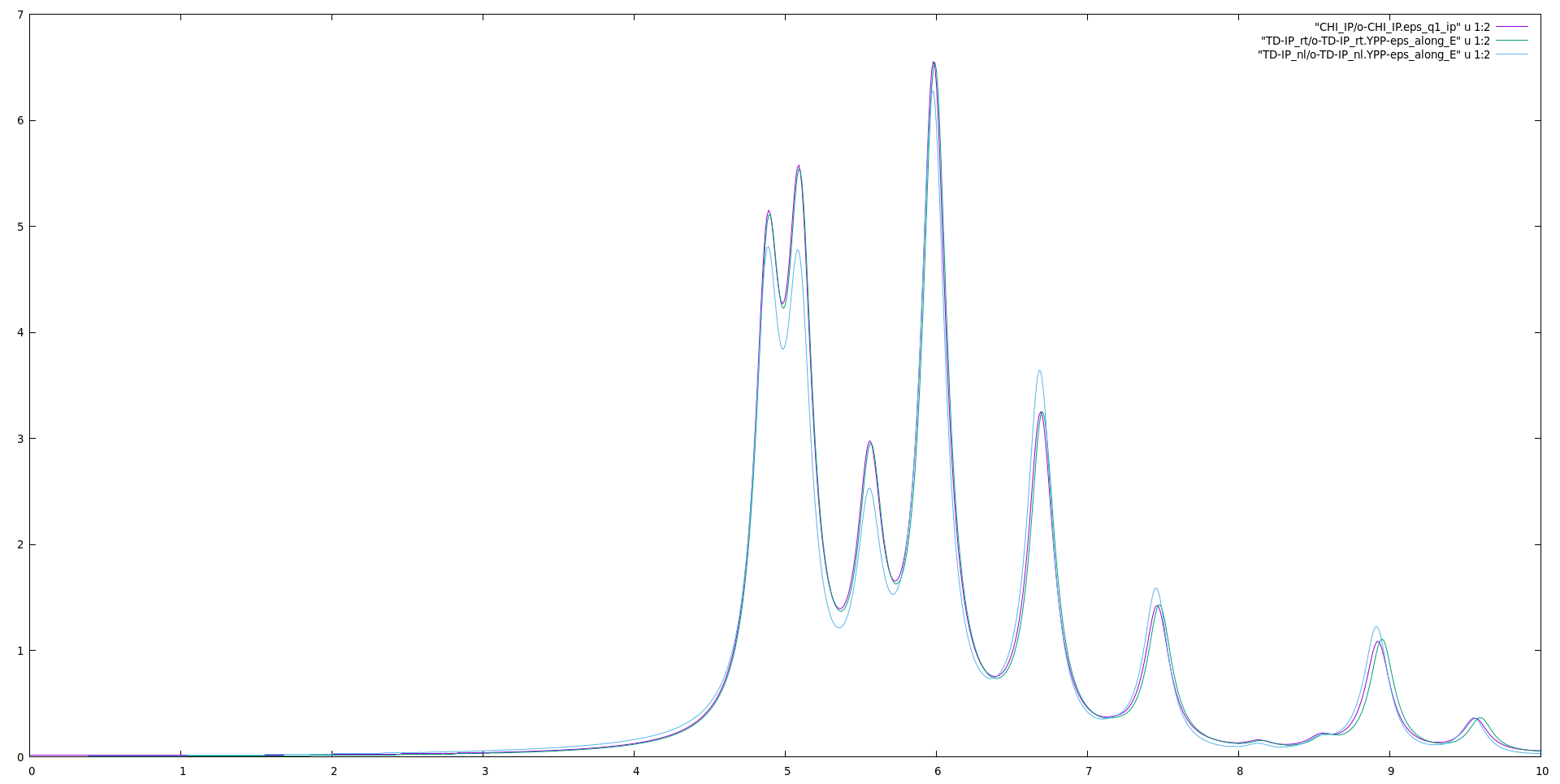
Now we can plot the dielectric constant and compare it with the linear response:
gnuplot plot "CHI_IP/o-CHI_IP.eps_q1_ip" u 1:2 w l rep "TD-IP_rt/o-TD-IP_rt.YPP-eps_along_E" u 1:2 w l rep "TD-IP_nl/o-TD-IP_nl.YPP-eps_along_E" u 1:2 w l
In the low energy part of the spectrum, the dielectric function obtained from the yambo_rt is closer to that obtained from the linear response approach. This may due to the fact that they share the same dipoles while in yambo_nl those are obtained numerically. Instead, in the high energy part of the spectrum, the dielectric function obtained from the yambo_nl is closer to that obtained from the linear response approach. Likely, this is due to the better integrator used.
To better understand these differences, one can use the inversion integrator with yambo_rt, the covariant dipoles in linear response.
References
- ↑ I. Souza, J. Íñiguez, and D. Vanderbilt, PRB 69, 085106 (2004)
- ↑ 2.0 2.1 2.2 C. Attaccalite and M. Gruning Rev. B, 88, 235113 (2013)
- ↑ C. Attaccalite, arXiv 1609.09639 (2017)
- ↑ D. Sangalli, and A. Marini EPL 110, 47004 (2015)